Le jeu de taquin, du côté de chez Galois

Écrit par Michel Coste
Version espagnole
Publié le 4 novembre 2011
Très illustré
15 - 30 minutes

SOMMAIRE

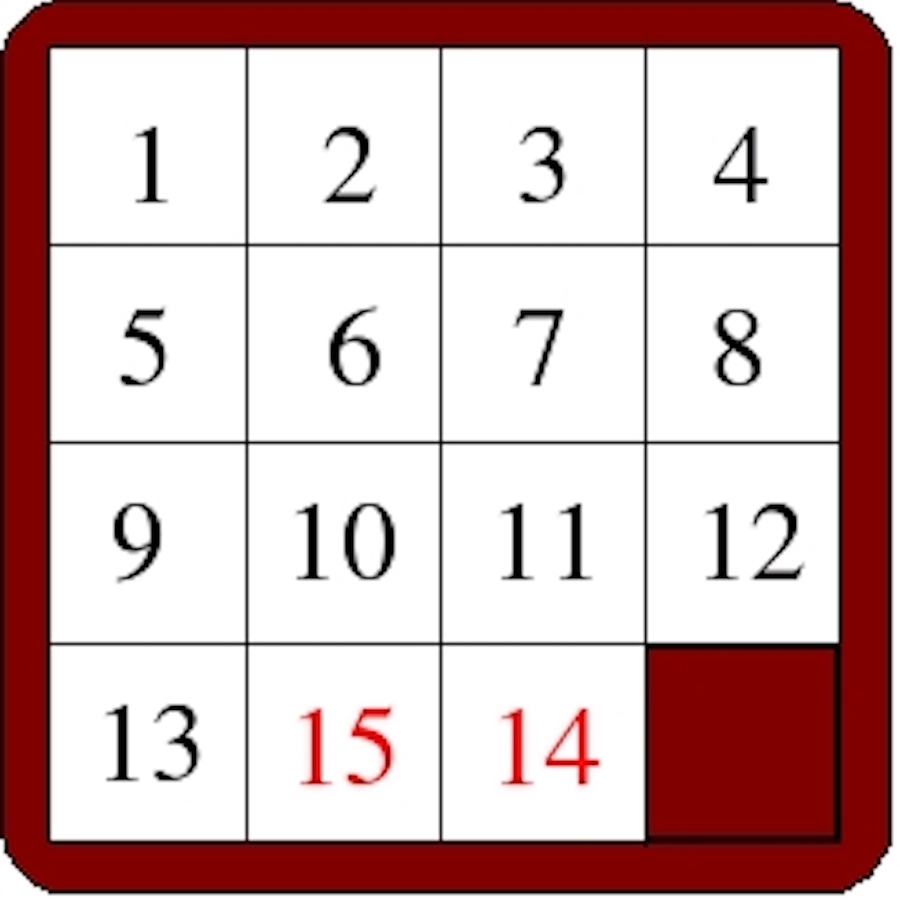
Vous connaissez peut-être le jeu de taquin. Ce jeu se compose d’un cadre contenant quinze plaques carrées numérotées de 1 à 15, laissant un espace dans lequel on peut faire coulisser une plaque voisine…

Lire l’article en ligne

ÉCRIT PAR

Michel Coste

Professeur - Université de Rennes

Partager

Commentaires

  1. Quelques idées pour les TIPE [Màj en cours] – MPI
    août 22, 2024
    7h37

    […] Jeu du taquin […]