
Où l’on verra que la nature tresse parfois les carottes.
En faisant mon marché, je me suis retrouvé soudain devant une vision surprenante : des carottes tressées ! Je n’avais jamais vu cela. Je décidai instantanément d’en faire un billet pour Images des Maths, et je les achetai donc sans hésiter. À la satisfaction des maraîchers, qui me dirent avoir pensé ne pas réussir à les vendre. Probablement que les ménagères et les ménagers raisonnables avaient cru à quelque OGM, ou bien s’étaient simplement dit que leur enlever la peau allait être un rude combat …
En tout cas, après les avoir lavées et mises un peu en valeur, je les ai prises en photo :

img1
Retournées et placées de plus à la verticale cela donna :

img2
Enfin, séparées (devinez laquelle il faut retirer en premier), elles se présentèrent ainsi :

img3
J’eus la confirmation que ce phénomène était suffisamment rare pour être digne de mention en surfant un peu sur la toile, et en trouvant un article de journal mentionnant une rencontre analogue.
En regardant la photo du journal ainsi que ma deuxième photo, on peut remarquer qu’en terre les trois têtes des racines se trouvaient quasiment à la verticale de leurs trois pointes 1En fait, il semble que ce soit une seule racine de carotte qui est photographiée dans le journal. Mais les deux bras de la racine principale sont si vigoureux et démarrent si près de sa tête que l’on a vraiment l’impression d’être face à trois carottes différentes.. C’est cela qui permet de parler de tresse au sens mathématique, comme l’explique cet article de Luis Paris. On y comprend en particulier que c’est précisément cette propriété qui permet de composer les tresses, et d’en faire un groupe.
Mais si on regarde mieux ces photos, on leur découvre un autre point commun : la tête de chaque racine se trouvait en terre quasiment à la verticale de sa propre pointe.
On dit alors qu’il s’agit d’une tresse pure. Est-ce un hasard, ou bien lors de la croissance des carottes, les déviations de la verticale produites par la rencontre d’obstacles ont tendance à être corrigées, et les extrémités des racines à se retrouver systématiquement à la verticale de leur tête ?
Je me demande aussi en quelle mesure on peut provoquer de tels tressages en semant des carottes de manière très rapprochée. Dans ce cas on pourrait jouer sur les effets de couleur, en combinant des carottes orange, jaunes, blanches ou rouge-betterave. Est-ce possible de produire aussi un tressage naturel d’au moins quatre carottes ?
Je pense qu’il serait intéressant d’imaginer une animation qui montre la croissance à partir des graines et jusqu’au résultat précédent. Mais comment obtenir des vérifications expérimentales du scénario ? Peut-être en faisant croître les carottes dans des substrats translucides ?
Pour finir, je voudrais expliquer pourquoi la tresse représentée par ces trois carottes ne peut pas être défaite 2Il s’agit de voir qu’elle ne peut pas être défaite au sens mathématique, c’est-à-dire en gardant ses extrémités fixées, en supposant les brins arbitrairement extensibles, et en ayant à chaque moment encore une tresse.. On peut bien sûr s’en convaincre expérimentalement, mais je voudrais indiquer ici une preuve mathématique. Il est nécessaire pour me suivre d’avoir lu de manière un peu attentive l’article de Luis Paris, et de savoir multiplier les matrices \(2×2\).
Écrivons le mot associé au diagramme de tresse tel qu’il est visible dans la troisième photo, en lisant du haut vers le bas :
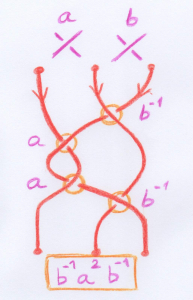
fig.
Chaque croisement est donc représenté par l’un des symboles \(a, b, a^{-1},
b^{-1}\), la convention choisie étant indiquée en haut du dessin. On obtient le mot
\(b^{-1}a^2 b^{-1}\).
Associons de la manière suivante une matrice à chacune des lettres \(a\) et \(b\) :
\[ a \rightarrow \left( \begin{array}{c}
1 & 1 \\ 0 &1
\end{array} \right), \: \: \:
b \rightarrow \left( \begin{array}{c}
1 & 0 \\ -1 &1
\end{array} \right).\]
Cette transformation s’étend en un {morphisme} {du groupe des tresses à trois brins vers le groupe} \(SL(2, \mathbb{Z})\) des matrices \(2 \times 2\) à coefficients entiers et de déterminant \(1\)3Il faut vérifier que cette définition est indépendante du mot représentant une tresse donnée. Cela peut se voir en sachant que l’on peut passer d’une expression à une autre pour une même tresse en utilisant un nombre fini de fois les égalités \(aba = bab\) et \(a a^{-1} = b b^{-1} = 1\). La deuxième suite d’égalités impose qu’on associe à l’inverse de chaque lettre l’inverse de la matrice qui lui correspond. Quant à la première égalité, il s’agit juste de vérifier qu’elle a encore lieu pour les matrices correspondantes..
On calcule alors que \(b^{-1}a^2 b^{-1}\) se transforme en
\(\left( \begin{array}{c}
3 & 2 \\ 4 &3
\end{array} \right)\) . Comme cette matrice est différente de la matrice identité, élément neutre du groupe \(SL(2, \mathbb{Z})\), cela montre que la tresse initiale n’est pas l’élément neutre du groupe des tresses à trois brins. C’est-à-dire qu’on ne peut pas la défaire.
————-
Et voilà à quoi peuvent aussi servir les mathématiques : à prouver que si l’on tressait des mèches de cheveux de la même manière que notre poignée de carottes, et bien on ne pourrait pas les défaire !
Post-scriptum
Merci à Luc Robbiano, qui m’a signalé une erreur d’inattention dans une première version de ce billet. J’y avais mal transcrit le mot associé au diagramme de tresse, ce qui m’a fait donner une explication plus simple, mais inapplicable au vrai mot, du fait que la tresse ne se défait pas.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.