
Quel est le meilleur trajet pour aller d’un point à un autre sur une île ?
Le numéro 59 (mai 2016) de Tangente hors-série contient une page de Philippe Boulanger (p. 49) qui commence ainsi :
Supposons que les transports aient un coût fini sur terre, proportionnel à la distance parcourue, et que les transports sur mer aient un coût nul. Pour aller d’un point \(A\) à un autre point \(M\) d’une île, vaut-il mieux aller directement sur terre et parcourir le segment \(AM\) entre ces deux points, ou aller du point \(A\) par le plus court chemin à la côte, longer la côte sur mer puis remonter de la côte jusqu’au point d’arrivée \(M\)?
Le premier exemple, d’où était parti Philippe Boulanger, est celui d’une île de forme circulaire ; la réponse est oui si \(M\) est à l’intérieur d’une certaine ellipse, non sinon (j’ai pris “vaut-il mieux” au sens strict ; au bord de l’ellipse, les deux trajets ont le même coût).
Un second exemple rompt avec l’image de l’île : une droite divise le plan en deux demi-plans, dont l’un représente la mer, et l’autre le continent. La question se transpose, et la réponse fait apparaitre une parabole au lieu d’une ellipse.
Le cas général proposé dans l’article de Philippe Boulanger est celui d’un ouvert convexe dans le plan (borné s’il s’agit d’une île) et des trajets d’un point \(A\) à un point \(M\), situés tous deux dans l’ouvert ; le coût d’un trajet à l’intérieur de l’ouvert est proportionnel à la distance parcourue, et il est nul en dehors de l’ouvert. Partant de \(A\), quels sont les points \(M\) qu’il vaut mieux joindre en restant à l’intérieur qu’en s’en échappant ? L’ensemble ces points \(M\), que je désigne par \(B(A)\), est visiblement un ouvert. En fait comme dans les deux exemples ci-dessous, c’est un ouvert convexe, et je vais expliquer pourquoi.
Je pars d’un ouvert \(G\) convexe. Pour simplifier, je suppose que sa frontière, \(F(G)\), a une tangente en chaque point. En chaque point de \(F(G)\), \(G\) est entièrement d’un côté de la tangente. On va voir qu’il en est de même pour \(B(A)\). Soit \(M\) un point frontière de \(B(A)\), et \(N\) un point de \(F(G)\) le plus proche de \(M\). On a donc \(AM = MN + d\), \(d\) étant la distance de \(A\) à \(F(G)\). Le point \(M\) est sur la parabole de foyer \(A\) dont la directrice est la droite \(D\) parallèle à la tangente en \(N\) à \(F(G)\), extérieure à \(G\), et à distance \(d\) de \(N\) (voir figure).
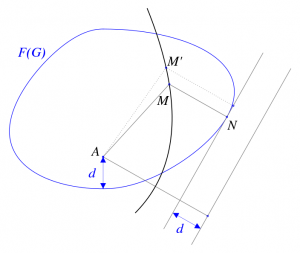
Tous les points \(M’\) de la parabole sont tels que \(AM’-d\) est égal à la distance de \(M’\) à la tangente en \(N\) à \(F(G)\). Or cette distance est supérieure à la distance de \(M’\) à \(F(G)\). La parabole est donc à l’extérieur de l’ensemble \(B(A)\). Cela entraîne que \(B(A)\) est entièrement d’un côté de la tangente en \(M\) à la parabole, qui est aussi une tangente à \(B(A)\). Cela veut dire que \(B(A)\) est convexe.
Si je désigne l’ouvert \(G\) par \(B_0\) et l’ouvert \(B(A)\) par \(B_1=B(A, B_0)\) pour bien marquer qu’il dépend de \(B_0\), je peux itérer la construction et considérer la suite des ouverts convexes emboités
\[B_{n+1} = B(A,B_n)\quad (n=0,1,2…)\]
Ces ouverts contiennent tous le disque ouvert de centre \(A\) tangent à la frontière de \(B_0, D(A,B_0)\), et les \(B_n\) convergent vers \(D(A, B_0)\) quand \(n\) tend vers l’infini.
Tout cela se généralise aisément au cas où, à la place du plan, on considère un espace euclidien de dimension finie. L’hypothèse que l’ouvert \(B_0\) est convexe tient au fait que, dans le problème initial, on parle de segment de droite joignant \(A\) et \(M\). Mais une seconde généralisation est de reprendre le problème en partant de \(B_0\) ouvert non nécessairement convexe. Cependant, pour éviter des discussions oiseuses dans le cas où \(B_0\) a plusieurs composantes connexes, je supposerai toujours \(B_0\) connexe. Partant d’un point \(A\) de \(B_0\), on définit comme précédemment \(B_1 = B(A, B_0)\) puis les ouverts emboités \(B_n\), qui sont tous connexes, et qui s’accumulent sur le disque \(D(A, B_0)\). L’étude avec \(B_0\) connexe est plus facile qu’avec \(B_0\) convexe.
On peut encore considérer à la place du plan un espace métrique \(E\), et prendre pour \(B_0\) un ouvert connexe dans \(E\). De nouveau, les \(B_n \quad (n=1,2,…)\) sont des ouverts connexes décroissants qui contiennent tous la plus grande boule ouverte de centre \(A\) contenue dans \(B_0\). A ce niveau de généralisation, il n’est pas tentant d’aller plus loin.
On peut alors spécialiser. Au lieu du plan et des trajets dans le plan, considérons un graphe avec ses sommets et ses arêtes, les trajets étant définis par des arêtes mises bout à bout, et la distance de deux sommets étant le nombre minimum d’arêtes dans un trajet qui les joint. Convenons que la mer, ici, recouvre une partie des arêtes, que les trajets maritimes aient un coût nul, et que les trajets terrestres aient pour coût leur longueur.
Le coût minimum d’un trajet entre deux sommets définit une nouvelle métrique. Partant d’un sommet \(A\), l’ensemble des sommets dont la distance à \(A\) est la même dans les deux métriques constitue l’ensemble \(B(A)\). Que peut-on en dire ?
On peut généraliser de nouveau, en pondérant les arêtes de manières diverses, et en comparant les métriques ainsi obtenues. La question est si naturelle qu’elle a certainement été étudiée. Cela permet-il un nouveau regard sur le problème de Philippe Boulanger ?
Post-scriptum
Philippe Boulanger, l’auteur du problème, est le fondateur et le premier directeur de la revue Pour la Science. Il m’a entretenu de son problème avant publication et son article fait allusion à nos conversations. Le cas où l’île est un domaine convexe était resté en suspens, avec une affirmation incorrecte de ma part : l’explication donnée ici que \(B(A)\) est convexe peut être convertie, au gré du lecteur, en démonstration formelle, sans hypothèse additionnelle. On voit que la frontière de \(B(A)\) est une enveloppe de paraboles comme \(F(G)\) est une enveloppe de droites.



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.