
Non, les plus jeunes d’entre nos lecteurs ne se la rappellent pas, et pour cause, on ne la leur a jamais enseignée, au moins si j’en juge par le peu de succès qu’a la question posée en Travaux Dirigés : « Expliquez-moi maintenant comment marche la preuve par 9 ! ».
Certains autres lecteurs se la rappellent peut-être, mais savent-ils pourquoi ça marche ?
Levons donc le voile, en cette date remarquable (pas tant que ça comme nous le verrons), sur la preuve par 9.
Et parmi nos lecteurs assidus, citons Nestor Burma 3personnage créé par Léo Malet. Il s’agit en l’occurence d’un passage de L’envahissant cadavre de la plaine Monceau, Les nouveaux mystères de Paris (II), (Bouquins, Robert Laffont) :
Je produis quelques talbins tentateurs. Elle qui a tant séduit, jadis, se laisse séduire à son tour, et après quelques chichis, me fournit un signalement des deux types – un grand et un petit, paraît-il- qui prouve, par neuf, que j’ai gaspillé mon fric.
Comme d’habitude, Nestor Burma a raison, même s’il passe sous silence la subtilité que la preuve par neuf n’est qu’une indication de la validité de son affirmation et n’est pas nécessairement une preuve irréfutable. Nous allons voir pourquoi.
La preuve par 9 enseignée à l’école élémentaire
Nous fixons maintenant de nouvelles règles de calcul. Dans celles-ci, nous décidons que 9 vaut 0. Les autres chiffres gardent leur valeur habituelle, mais, bien sûr, quand nous les ajoutons ou les multiplions, nous nous rappelons que 9 vaut 0, ce que nous noterons par 9≡0. Par exemple 5+4≡9≡0, 10≡9+1≡0+1≡1, ou encore 14≡9+5≡0+5≡5.
Plus compliqué,
- \(28≡3×9+1≡0+1≡1,\)
- \(228≡2×10×10+28≡2×1×1+1≡2+1≡3\)
- \(1000≡10×10×10≡1×1×1≡1.\)
Vous l’avez compris et vous pouvez le vérifier sur ces exemples : avec ces règles, on identifie un nombre via le symbole ≡ à la somme de ces chiffres en annulant les 9 apparaissant dans cette somme, puis cette somme de nouveau à la somme de ses chiffres, et ainsi de suite jusqu’à ce qu’on trouve un nombre entre 0 et 8, qu’on appelle son équivalent. Et comme toutes les puissances de 10 sont équivalentes à 1, on constate que tout nombre est équivalent, avec ces règles, au reste de sa division par 9.
Par exemple,
\[7689076543765439≡7+6+8+7+(6+3)+7+(6+3)≡1+7≡8,\]
ce qui est un calcul du fait que l’équivalent de \(7689076543765439\) est \(8\) (et donc que le reste de la division par 9 de ce nombre est 8).
A ce jeu-là, c’est une conséquence de ce qui suivra, un multiple de \(9\) est identifié à \(0\) et tout nombre identifié à \(0\) est un multiple de \(9\). Comme n’importe quel nombre est identifié à la somme de ses chiffres, cela rappelle à Georges Perec 4Je me souviens, (Hachette, collection P.O.L., 1978)
Je me souviens que tous les nombres dont les chiffres donnent un total de neuf sont divisibles par neuf (parfois je passais des après-midi à le vérifier…)
et nous permet de vérifier qu’un nombre est multiple de \(9\) si et seulement si la somme de ses chiffres est multiple de \(9\).
Et patatras, \( 2009 \equiv 2\) n’est pas divisible par \(9\). Il eût fallu attendre \(2016\) pour que la date du \(9-9-2016\) à \(9H09\) soit complètement divisible par \(9\)…
En général, on enseigne la preuve par \(9\) comme moyen de vérification partielle des multiplications, dont le calcul à la main engendre beaucoup d’erreurs. L’idée est de substituer les nombres dont on calcule le produit par leurs équivalents. L’équivalent du résultat doit être égal au résultat du calcul sur les équivalents pour valider la preuve par \(9\).
Pour vérifier que \(4289\times27=115803\) on dessine une croix, en haut de la croix on place l’équivalent de \(4289\), c’est-à-dire \(5\), en bas l’équivalent de \(27\), c’est-à-dire \(0\), à gauche le produit des deux équivalents \(5\times0=0\) et à droite, l’équivalent du résultat qu’on a trouvé, c’est-à-dire \(7+8+3\equiv 0\).
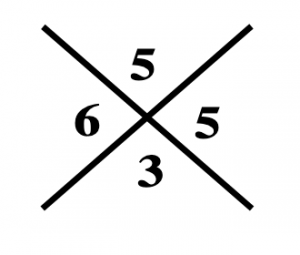
la croix de la preuve par 9 pour la multiplication
Les deux coïncident. La preuve par \(9\) est validée.
Voici un autre exemple: \(5315\times732=3890480\) et la croix correspondante qui indique que la preuve par \(9\) n’est pas validée.

une deuxième croix
Qu’est-ce que cela prouve? Prenons le premier exemple, on voit facilement que des résultats comme \(1503\), \(0\), même s’ils sont impossibles pour des raisons d’ordre de grandeur valident la preuve par \(9\), ou encore \(176823\).
La preuve par \(9\) dit précisément que nous avons trouvé le bon résultat à un multiple de \(9\) près,
ce qui, vu l’économie de calculs réalisés, n’est pas si mal.
Et surtout,
si la preuve par \(9\) est fausse, le calcul est faux,
en admettant bien sûr que le calcul très simple de la preuve par \(9\) soit juste.


Et maintenant, un peu de justifications
De quoi s’agit-il ? Décidons d’identifier deux entiers quand leur différence est un multiple de \(9\),
\(13\) est alors identifié à \(4\), car \(13=1\times9+4\), \(10\) à \(1\),
\(99=11\times9\) à \(0\) et en fait tout entier est identifié au reste de la division euclidienne,
avec reste donc, par \(9\). Nous noterons cette identification: \(13 \sim 4\). Par définition,
les nombres identifiés à \(0\) sont les multiples de \(9\).
La remarque décisive démontrée ci-dessous est que cette identification est compatible à la somme et au produit.
Pour vérifier la compatibilité à la somme, il faut vérifier que si \( k\) et \(k’\) sont identifiés à \(r\) et \(r’\), alors \(k+k’\) est identifié à \(r+r’\). Ecrivons \(k=9\times a+r\), et \(k’=9\times a’+r’\), alors \(k+k’=9\times(a+a’)+r+r’\) et on voit bien que \(k+k’\sim r+r’\).
De plus, \(k\times k’\) est aussi identifié à \(r\times r’\) car on a l’égalité \(k\times k’=9\times(9\times a\times a’+r’\times a+r\times a’)+r\times r’\), qui montre la compatibilité à la multiplication.
Concrètement, comme \(73\sim 1\), et \(17\sim 8\), alors \((73+17)\sim 8+1\sim 9 \sim 0\). De même pour le produit: \((73\times17)\sim 1\times8\sim 8\). On peut ainsi calculer le reste de la division de \(73\times17\) par \(9\) sans calculer le résultat du produit.
Grâce à ces compatibilités, on remarque que \(10\sim 1\), \(100\sim 1\times1\), …, \(10^r\sim 1\) et donc n’importe quel nombre écrit en base \(10\)
\[10^r a_r + 10^{r-1} a_{r-1}+ \ldots + a_1 \times 10 + a_0\]
est identifié à \(a_r +a_{r-1}+ \ldots +a_1 +a_0\) c’est-à-dire à la somme de ses chiffres.
Prenez par exemple: \(1234567890=10^9+ 2\times 10^8+ 3\times 10^7+4\times 10^6+5 \times 10^5+ 6\times 10000 + 7\times 1000+8\times 100+9\times 10\) est identifié à \(0\). Ce nombre est donc divisible par \(9\). La boucle est bouclée: l’identification faite ici est bien la même qui était enseignée à l’école élémentaire pour effectuer la preuve par \(9\). Et d’ailleurs, puisque c’est la même chose, nous allons la noter de la même façon, avec un symbole \(\equiv\).
La preuve par \(9\) consiste à vérifier les calculs après identification, puisque cette identification est compatible aux opérations naturelles. Reprenons l’exemple précédent.
Il s’agit de vérifier que \(4289\times27\equiv 0\) puisque \(4289 \equiv 5\), \(27\equiv 0\). On démontre ainsi les propriétés de cette preuve par \(9\) énoncées plus haut. Si la preuve par \(9\) est juste, le résultat est juste à un multiple de \(9\) près.
Remarquablement, l’utilisation de cette preuve est un exemple de condition nécessaire non suffisante, et sans doute un des premiers exemples que l’on rencontrait dans sa scolarité. Pour qu’un calcul soit juste, il faut que la preuve par \(9\) soit validée, mais ce n’est pas suffisant. Il se peut que la preuve par 9 soit juste et le calcul faux. En revanche, comme nous l’avons déjà rappelé, si la preuve par \(9\) n’est pas juste, le calcul est faux.
Et, cela arrive parfois: notre calcul est juste mais nous nous sommes trompés dans le calcul de la preuve par \(9\) qui n’est alors pas valide…
Pourquoi se limiter à la multiplication ?
Il n’y a aucune raison de se limiter à la vérification des multiplications.
Faisons la preuve par \(9\):
-
- d’une somme: \(56789+12300004567=12300061356\). On calcule: \(56789\equiv 8\), \(12300004567\equiv 1\) et \(12300061356\equiv 0\), ce qui est valide car \(0\equiv 8+1.\)
-
-
- d’une soustraction: pour faire la preuve par \(9\) de \(12300061356-56789=12300004567\), on teste le résultat de la somme: \(12300004567+56789\).
- d’une division euclidienne: \(12300004567\) divisé par \(56789\) donne un quotient de \(216591\) et un reste de \(18268\), ce qu’on exprime par \(12300004567=56789\times216591+18268\). C’est ce résultat qu’on vérifie: \(216591\equiv 6\), \(18268\equiv 7\), de sorte que \(56789\times216591+18268\equiv 8\times6+7\equiv 1\) et on a bien \(12300004567\equiv 1\).
-
Et la preuve par un autre entier ?
Jouons au jeu précédent avec \(11\): nous décidons maintenant que \(11\) vaut \(0\). Alors on identifie \(10\) à \(11-1=-1\), \(100=10\times10\) à \((-1)^2=1\), \(1000\) à \((-1)^3=-1\), donc les puissances paires de \(10\) à \(1\) et les puissances impaires de \(10\) à \(-1\) et on identifie un entier à la somme alternée de ses chiffres \( 1234567890\) est alors identifié à \(-1+2-3+4-5+6-7+8-9+0\) c’est-à-dire à \(-5\) et donc aussi à \(6=11-5\), nombre identifié à \(-5\).
Nous laissons au lecteur le soin d’expliciter ce qu’est la preuve par \(11\). Si les preuves par \(9\) et par \(11\) d’un calcul sont justes, alors ce calcul est juste à un multiple de \(99\) près, car \(11\) et \(9\) sont premiers entre eux (sans diviseur commun).
Il n’y a pas non plus de raison de se borner à la preuve par \(9\) et \(11\), même si, on l’a compris, \(9\) et \(11\) sont particulièrement adaptés à notre notation décimale.
Que donne la preuve par \(2\) ? Eh bien cela consiste à identifier tous les entiers pairs à \(0\) et les entiers impairs à \(1\). Faire la preuve par \(2\) consiste alors à vérifier que le produit de deux nombres impairs est impair, que le produit d’un nombre pair par un autre nombre est pair, que la somme de deux nombres impairs est paire, etc …
Que donne la preuve par \(1\) ? Pas grand chose puisqu’alors tous les nombres sont identifiés à \(0\) et la preuve par \(1\) est toujours juste quel que soit le calcul, puisque par exemple \(0+0=0\) !
Et maintenant, la preuve par \(0\) ? Dans ce cas \(0\) est identifié à \(0\) et … c’est tout. On ne change strictement rien. Faire la preuve par \(0\) consiste à refaire les calculs à l’identique.
C’est en jouant au même jeu avec \(5\) que la mathématicienne Sophie Germain a démontré, au début du 19e siècle que si \(x,y,z\) sont des solutions entières de l’équation
\[x^5+y^5=z^5,\]
alors \(x\) ou \(y\) ou \(z\) sont multiples de \(5\). Cet énoncé de Sophie Germain fut une première étape importante pour le cas correspondant à l’exposant \(5\) du théorème de Fermat.
Post-scriptum
Remerciements : par ordre alphabétique, à Michèle Audin et à Christiane Huyghe pour leurs conseils de rédaction de ce texte.





13h39
9 sept 2009
Voir les commentaires
https://images-archive.math.cnrs.fr/Ceci-n-est-pas-une-preuve.html?var_mode=calcul#commentaires