Voici un extrait de courrier des lecteurs que je viens de recevoir et auquel je réponds par ce billet.
J’ai été interpellé par une élève de seconde qui m’a expliqué qu’on l’avait arnaqué au collège lorsqu’on lui avait construit la multiplication.
Elle m’a en effet dit que : “(+2)+(+2)+(+2)=3*(+2)” ou “(-2)+(-2)+(-2)=3*(-2)” lui convenait et qu’elle comprenait, là, le sens du “3”. C’est à dessein que “3” n’a pas de signe.
En revanche, du coup, dans cette construction de la multiplication, “(-3)*(-2)” ne pouvait pas être construit : quel est le sens de ce “MOINS 3” ?
Je suis son professeur de sciences physiques et je ne sais pas quoi lui répondre.
La notion de nombre est un sacré problème. Un des buts de l’école primaire est celui de permettre à l’élève de savoir compter avant de rentrer au collège. 1, 2, 3… bonbons, stylos, crayons… beaucoup d’objets sont utilisés pour fixer dans nos têtes les premiers nombres, peut-être jusqu’à cent, et se familiariser avec eux. Parfois, tous petits, nous chantons les nombres. Nous les voyons aussi écrits un peu partout : sur des calendriers, sur le compteur de nos voitures, sur les réveils, sur les ordinateurs, au bas des pages de nos livres, sur une règle qui traîne sur le bureau, sur les bouteilles dans la cuisine… Les doigts de nos mains nous intriguent dès notre plus jeune âge comme pour nous suggérer qu’il y a là une idée à trouver.
Un monde sans nombres ? Plus de notes, plus de bulletins… plus de chagrins et plus de réveils qui sonnent le matin pour nous dire qu’il est l’heure de se lever.
Un monde sans nombres ne serait pas le monde actuel. Effacer les nombres de notre culture, signifierait effacer tout d’un coup le monde qui nous entoure actuellement.
Il a fallu des siècles pour passer des nombres entiers naturels aux nombres relatifs, puis aux nombres rationnels, puis aux nombres irrationnels, puis aux nombres complexes.
Quelle découverte cette notion de nombre ! Si profonde et si proche – à portée de main… – qu’elle reste une des plus belles inventions de la pensée humaine. Tout comme la roue.
Bertrand Russell dans son livre « Introduction to Mathematical Philosophy » 1Bertrand Russell, « Introduction to Mathematical Philosophy », George Allen and Unwin, London, UK. Reprinted, John G. Slater (intro.), Routledge, London, UK, 1993. dit que « il a fallu beaucoup de siècles pour découvrir qu’un couple de faisans et un couple de jours sont la même expression du nombre 2 ; le degré d’abstraction que ceci comporte n’est certainement pas léger. Ainsi la découverte du nombre 1 a dû être difficile. Le zéro est une découverte plus récente ; les Grecs et les Romains n’avaient pas ce chiffre ». Et plus loin, le philosophe anglais ajoute « Toute la mathématique pure traditionnelle, y compris la géométrie analytique, peut être considérée comme formée de propositions qui portent sur les nombres entiers naturels ». Ouf ! Je pense que notre jeune lectrice comprendra bien qu’elle a mis le doigt sur une notion très profonde, celle de nombre. Rien de plus sain donc d’avoir besoin de vouloir les apprivoiser et de bien comprendre les opérations qui les mettent en scène. Il y a une vaste littérature mathématique sur ce sujet et beaucoup de grands mathématiciens (Dedekind, Frege, Peano,..) ont pris les nombres comme base afin de bâtir sur ces fondements l’édifice mathématique.
Le grand philosophe B. Russell consacre les cinquante premières pages du livre précédemment cité à la notion de nombre et au passage d’un nombre n au suivant n+1.
Encore une fois, l’idée de compter, de passer d’un nombre à son successeur, est tellement ancrée dans nos habitudes qu’elle passe parfois inaperçue, comme un fait sans importance. Russell écrit : « En réalité, compter, bien que familier, est du point de vue logique une opération très complexe ».
Pour aller un peu plus loin dans l’histoire des mathématiques, le grand mathématicien suisse L. Euler avait eu recours, pour expliquer les règles des signes dans l’ensemble des nombres relatifs, à un raisonnement peu convaincant que voici 2Richard Courant – Herbert Robbins, « What’is Mathematics ? An Elementary Approach to Ideas and Methods », Oxford University Press, New York 1941, second edition revised by Ian Stewart (1996). Pour démontrer que (-1)(-1) « doit » être égal à +1 il raisonna de la façon suivante : (-1)(-1) doit être ou +1 ou -1, et il ne peut pas être -1 car (-1) = (+1)(-1).
Pour apporter une réponse à la question de cette jeune élève, je suis allé fouiller dans ma bibliothèque et j’ai trouvé un livre en italien qui m’avait marqué très jeune : « I numeri » (Les nombres) de Emma Castelnuovo. 3Emma Castelnuovo, « La via della matematica, I NUMERI » , Ed. La Nuova Italia, 1974.
Madame Castelnuovo a été l’une des plus grandes didacticiennes des mathématiques en Italie et reconnue à l’étranger pour ses travaux sur l’enseignement des mathématiques. Elle est née le 12 décembre 1913 à Rome, où elle a obtenu sa maîtrise en 1936 avec notamment un mémoire de géométrie algébrique. Après avoir travaillé à la (magnifique) bibliothèque du département de mathématiques de l’Université de Rome « La Sapienza » – département qui porte le nom de son père Guido Castelnuovo – elle a enseigné au Lycée « Torquato Tasso » de Rome jusqu’en 1979. Elle a donné des cours jusqu’à l’âge de 93 ans !
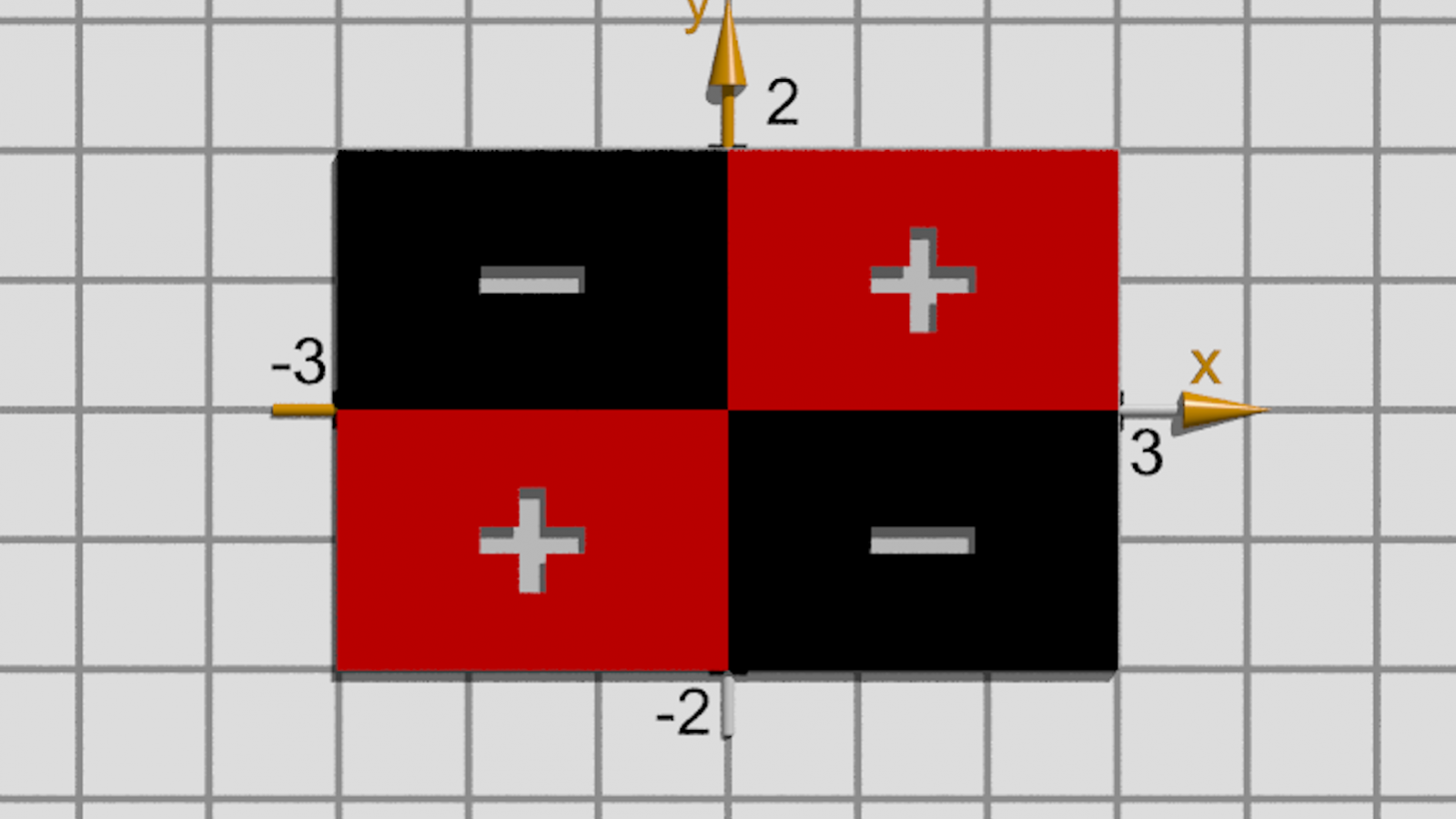
Dans son livre « I numeri », elle invite le lecteur à un autre point de vue que celui proposé dans le courrier de notre lecteur, celui de se représenter géométriquement le produit de deux nombres entiers relatifs et à prendre un rectangle en carton, par exemple de dimensions 2 et 3 (celles qui nous intéressent dans le courrier plus haut cité). Supposons que les faces de ce carton soient de couleurs différents : l’une rouge et l’autre noire. Nous ferons la convention suivante : l’aire de la face rouge est positive et celle de la face noire négative. Si les dimensions du rectangle sont 2 et 3, son aire sera, en valeur absolue, égale à 6. D’un point de vue « relatif », nous dirons que l’aire est +6 si elle se présente côté rouge et -6 si elle se présente côté noir. Disposons maintenant le rectangle dans le premier quadrant (c.f. figure ci-dessous) de telle sorte qu’apparaisse la face rouge, c’est-à-dire la face positive ; son aire sera alors +6. Puisque les dimensions dans ce cas sont +2 et +3 on pourra alors écrire :
-
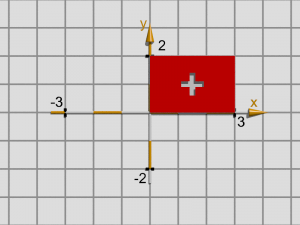
Premier quadrant
Faisons maintenant une symétrie axiale d’axe Oy ; le rectangle passera dans le deuxième quadrant et nous verrons le côté noir (c.f. figure ci-dessous), c’est-à-dire son aire sera négative et égale à -6. Dans ce cas ses dimensions sont -2 et +3. On a alors :
-
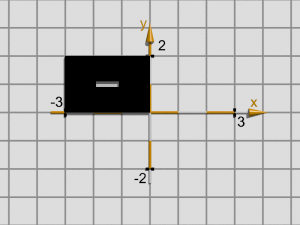
Deuxième quadrant
Par une symétrie par rapport à l’axe Ox, le rectangle va à nouveau apparaître côté rouge et son aire va être +6 alors que ses dimensions sont dans ce cas – 2 et – 3. On a alors :
-
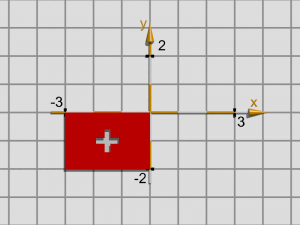
Troisième quadrant
Par une autre symétrie par rapport à l’axe Oy le rectangle finira par se trouver dans le quatrième quadrant et nous allons voir son côté noir, c’est-à-dire, la partie négative alors que ces dimensions sont +2 et -3. On a alors :
-
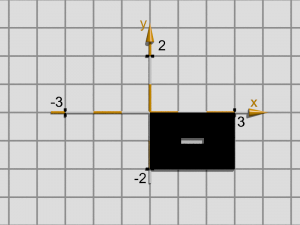
Quatrième quadrant
Voici une petite animation qui permet de visualiser les transformations décrites ci-dessus :
Les mathématiques sont peut-être « l’art des liens ».


12h15
Voir les commentaires .