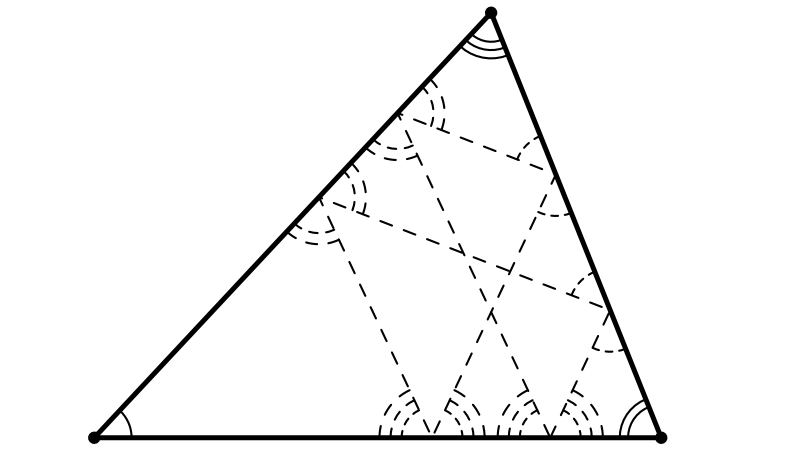
Une nouvelle extension de l’énigme : avec n terriers
.
Un renard, Fox, est dans l’un de n terriers alignés (n ≥ 2).
Chaque nuit, Fox passe dans un terrier contigu à celui qu’il occupe.
Chaque jour, nous pouvons regarder dans l’un des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox.
.
.
.
Solution du premier défi
Rappel du défi
Un renard, Fox, est dans l’un de cinq terriers alignés.
Chaque nuit, Fox passe dans un terrier contigu à celui qu’il occupe.
Chaque jour, nous pouvons regarder dans l’un des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox
Premier temps : si Fox est à l’origine dans un terrier dont le numéro est pair
Fox est donc soit en 2, soit en 4.
Quand nous regardons en 2, si Fox s’y trouve, c’est terminé, sinon, c’est qu’il était en 4.
Nous allons alors l’empêcher de revenir vers 2 en regardant ensuite dans le terrier 3, si Fox s’y trouve, c’est terminé, sinon, c’est qu’il est passé du 4 dans le 5.
Cependant, du terrier 5, la seule possibilité qu’il a est d’aller dans le terrier 4 et en regardant enfin dans le terrier 4, on le trouve.
Conclusion Dans ce premier temps, la suite « 2, 3, 4 » est une stratégie qui permet de trouver Fox.
Remarque De façon analogue, par symétrie, la suite « 4, 3, 2 » aussi.
Second temps : si Fox est à l’origine dans un terrier dont le numéro est impair
Fox est donc soit en 1, soit en 3, soit en 5.
On applique la stratégie « 2, 3, 4 » ou « 4, 3, 2 ». À l’issue, Fox s’est déplacé d’un nombre impair de terriers (par trois fois d’un terrier) ce qui nous permet de conclure que, maintenant, Fox se trouve bel et bien dans un terrier dont le numéro est pair. Nous sommes donc ramenés dans le premier temps où nous trouvons Fox par « 2, 3, 4 » ou par « 4, 3, 2 ».
Conclusion Dans ce deuxième temps, faire suivre « 2, 3, 4 » ou « 4, 3, 2 » de « 2, 3, 4 » ou « 4, 3, 2 » permet de trouver Fox.
Conclusion globale
Nous avons quatre stratégies pour trouver Fox, à savoir « 2, 3, 4, 2, 3, 4 », « 2, 3, 4, 4, 3, 2 », « 4, 3, 2, 2, 3, 4 » et « 4, 3, 2, 4, 3, 2 ».
Des stratégies plus longues sont correctes aussi : on peut insérer n’importe quelle suite avant ou après l’une de ces quatre suites ; on peut même insérer n’importe quelle suite d’un nombre pair de termes au « milieu » de n’importe laquelle de ces quatre suites ; on peut remplacer « 2, 3, 4 » par « 2, 3, 3, 3, 4 » ; etc.
Cependant, trouver une stratégie plus courte est impossible. Malheureusement, nous n’avons pas de « jolie démonstration » de ceci et n’en avons qu’une preuve dans laquelle nous regardons toutes les stratégies en cinq observations (il s’agit d’un algorithme « glouton » ; il existe \(5^5\) stratégies possibles a priori : nous faisons 5 observations parmi 5 terriers possibles) et nous concluons que chacune laisse à Fox une possibilité de se soustraire à notre regard.
Preuve par "Maple 5.0"
En préambule, on définit deux fonctions : g qui permet de passer d’un entier à son prédécesseur ; et d qui permet de passer d’un entier à son successeur.
> g:=proc(x);
> RETURN(x-1)
> end:
> d:=proc(x);
> RETURN(x+1)
> end:
On cherche d’abord les stratégies valables en 5 observations
Dans le programme suivant, tous les trajets de Fox sont numérotés par l’indice n et stockés dans PF[n]. Il apparaît que nvarie de 1 à 42 (nous avons 42 trajets possibles).
> n:=1:
> for Fox1 from 1 to 5 do
> for f1 in {g,d} do
> if f1(Fox1)>0 and f1(Fox1)<6 then Fox2:=f1(Fox1):
> for f2 in {g,d} do
> if f2(Fox2)>0 and f2(Fox2)<6 then Fox3:=f2(Fox2):
> for f3 in {g,d} do
> if f3(Fox3)>0 and f3(Fox3)<6 then Fox4:=f3(Fox3):
> for f4 in {g,d} do
> if f4(Fox4)>0 and f4(Fox4)<6 then Fox5:=f4(Fox4):
> PosFox:=Fox1,Fox2,Fox3,Fox4,Fox5: PF[n]:=[PosFox]: n:=n+1
> fi: od:
> fi: od:
> fi: od:
> fi: od:
> od:
Nous récupérons les 42 déplacements possibles du renard au bout de 5 déplacements stockés comme une liste des 5 positions successivement occupées …
Par exemple, PF(1) est [1, 2, 3, 4, 5] et se lit : « Fox est au terrier 1 au départ, puis il passe en 2, puis en 3, puis en 4, et enfin en 5 ».
D’un autre côté, nous stockons aussi les 3 125 stratégies …
> n:=1:
> for i1 from 1 to 5 do
> for i2 from 1 to 5 do
> for i3 from 1 to 5 do
> for i4 from 1 to 5 do
> for i5 from 1 to 5 do
> Strat[n]:=[i1,i2,i3,i4,i5]:n:=n+1
> od:
> od:
> od:
> od:
> od:
Une stratégie où l’on regarde 2 fois en 2 puis 3 fois en 4 est notée [2, 2, 4, 4, 4]. Ces stratégies sont numérotées de 1 à 3 125.
Une stratégie parmi les 3 125 (n allant de 1 à 3 125) est valable si pour chacun des 42 trajets de Fox possibles (k allant de 1 à 42), on peut trouver un indice i (i allant de 1 à 5) commun entre la stratégie et le trajet du renard pour lequel les positions en cet indice soient égales.
> for n from 1 to 3125 do
> valid[n]:=1:
> for k from 1 to 42 do
> val[n,k]:=0:
> for i from 1 to 5 do
> if PF[k][i]=Strat[n][i] then val[n,k]:=1 fi:
> od:
> valid[n]:=valid[n]*val[n,k]:
> od:
> if valid[n]=1 then print(Strat[n]) fi:
> od:
Le programme s’est arrêté sans avoir révélé de stratégie valable, ce qui indique qu’il n’existe aucune stratégie permettant de trouver automatiquement Fox en 5 observations.
Notons que nous avons validé quatre stratégies pour trouver Fox en six observations, mais nous n’avons pas prouvé qu’il n’en existe pas d’autre. Là encore, point de « jolie démonstration » et nous n’avons qu’une preuve dans laquelle nous regardons toutes les stratégies en six observations (il s’agit là encore d’un algorithme « glouton » ; il existe \(5^6\) stratégies possibles a priori : nous faisons 6 observations parmi 5 terriers possibles) et nous concluons que seules les quatre stratégies données sont valables pour trouver Fox.
Preuve par "Maple 5.0"
On recommence pour chercher les stratégies valables en 6 observations
> n:=1:
> for Fox1 from 1 to 5 do
> for f1 in {g,d} do
> if f1(Fox1)>0 and f1(Fox1)<6 then Fox2:=f1(Fox1):
> for f2 in {g,d} do
> if f2(Fox2)>0 and f2(Fox2)<6 then Fox3:=f2(Fox2):
> for f3 in {g,d} do
> if f3(Fox3)>0 and f3(Fox3)<6 then Fox4:=f3(Fox3):
> for f4 in {g,d} do
> if f4(Fox4)>0 and f4(Fox4)<6 then Fox5:=f4(Fox4):
> for f5 in {g,d} do
> if f5(Fox5)>0 and f5(Fox5)<6 then Fox6:=f5(Fox5):
> PosFox:=Fox1,Fox2,Fox3,Fox4,Fox5,Fox6:
> PF[n]:=[PosFox]: n:=n+1
> fi: od:
> fi: od:
> fi: od:
> fi: od:
> fi: od:
> od:
Nous récupérons les 72 déplacements possibles du renard au bout de 6 déplacements …
D’un autre côté, nous stockons aussi les 15 625 stratégies …
> n:=1:
> for i1 from 1 to 5 do
> for i2 from 1 to 5 do
> for i3 from 1 to 5 do
> for i4 from 1 to 5 do
> for i5 from 1 to 5 do
> for i6 from 1 to 5 do
> Strat[n]:=[i1,i2,i3,i4,i5,i6]:n:=n+1
> od:
> od:
> od:
> od:
> od:
> od:
Une stratégie parmi les 15 625 (n allant de 1 à 15 625) est valable si pour chacun des 72 trajets de Fox possibles (k allant de 1 à 72), on peut trouver un indice i (i allant de 1 à 6) commun entre la stratégie et le trajet du renard pour lequel les positions en cet indice soient égales.
> for n from 1 to 15625 do
> valid[n]:=1:
> for k from 1 to 72 do
> val[n,k]:=0:
> for i from 1 to 6 do
> if PF[k][i]=Strat[n][i] then val[n,k]:=1 fi:
> od:
> valid[n]:=valid[n]*val[n,k]:
> od:
> if valid[n]=1 then print(Strat[n]) fi:
> od:
[2, 3, 4, 2, 3, 4]
[2, 3, 4, 4, 3, 2]
[4, 3, 2, 2, 3, 4]
[4, 3, 2, 4, 3, 2]
Nous obtenons ci-dessus les 4 seules stratégies permettant de trouver assurément Fox en 6 observations.
On peut trouver une solution vidéo sur Logically yours, Mohammed Ammar2 Seemingly impossible fox puzzle ; fox in a hole (consulté le 17 octobre 2023)
Remarque Pour ce problème « Fox and Holes », nous nous sommes efforcés de justifier qu’il n’existe pas de stratégie plus courte que celles proposées et aussi de déterminer toutes les stratégies les plus courtes.
Quelques remarques sur la solution et les algorithmes gloutons précédemment évoqués
L’algorithme glouton, par conception, est loin d’être économique. Par exemple, quand pour la première observation on regarde en 2, il envisage aussi que pour la seconde observation, on regarde en 1, ce qui est complètement idiot : en effet, ayant observé en 2 lors de la première observation,
• s’il y est, c’est terminé et il n’est pas nécessaire de poursuivre,
• s’il n’y est pas, il ne sera assurément pas en 1 lors de la deuxième observation (en effet, il ne peut se rendre en 1 que s’il était en 2 précédemment) et la deuxième observation est donc stérile.
Observons maintenant de plus près la solution « 2, 3, 4, 2, 3, 4 » et ce que cette stratégie opère sur les possibles positions du renard :
- Le renard est initialement en l’un des terriers 1, 2, 3, 4 ou 5.
- Jour 1 Quand on observe en 2, si on n’a pas trouvé le renard, il est en l’un des terriers 1, 3, 4 ou 5.
- Nuit 1 Le renard se déplace pour aller dans l’un des terriers 2, 3, 4 ou 5.
- Jour 2 Quand on observe en 3, si on n’a pas trouvé le renard, il est en l’un des terriers 2, 4 ou 5.
- Nuit 2 Le renard se déplace pour aller dans l’un des terriers 1, 3, 4 ou 5.
- Jour 3 Quand on observe en 4, si on n’a pas trouvé le renard, il est en l’un des terriers 1, 3 ou 5
- Nuit 3 Le renard se déplace pour aller dans l’un des terriers 2 ou 4.
- Jour 4 Quand on observe en 2, si on n’a pas trouvé le renard, il est en le terrier 4.
- Nuit 4 Le renard se déplace pour aller dans l’un des terriers 3 ou 5.
- Jour 5 Quand on observe en 3, si on n’a pas trouvé le renard, il est en le terrier 5.
- Nuit 5 Le renard se déplace pour aller en le terrier 4.
- Jour 6 Quand on observe en 4, on le trouve forcément !
De cette observation, on pourrait remplacer l’algorithme glouton par un algorithme qui ne considère que les positions possibles du renard !
Cependant, si on décidait de ne considérer que des observations telles que le cardinal des positions possibles du renard décroisse de nuit en nuit, cela tiendrait d’une heuristique car il n’a jamais été démontré que cette suite devait forcément être décroissante (même si elle décroît effectivement dans l’exemple considéré, mais pas strictement).
Post-scriptum
La rédaction d’Images des maths, ainsi que les auteurs, remercient pour leur relecture attentive, les relecteurs dont le pseudonyme est le suivant -projetmbc, Walter et Gautier Dietrich.
ÉCRIT PAR
François Dessenne
Maître de conférences - Université de Lille
Jean Fromentin
Professeur - Université du Littoral Côte d’Opale, Calais
Denis Vekemans
Maître de conférences - INSPÉ Lille Nord de France - Université du Littoral Côte d'Opale
