14 juillet : sommes-nous cocardiers ?

Un petit bavardage sur les différentes dénominations des théorèmes.

Une anecdote

Voici, en substance, ce qu’affirma le mathématicien Allemand Michael Rapoport, dans un français parfait, au cours d’un exposé qui ne l’était pas moins, à la conférence internationale donnée en l’honneur de Gérard Laumon, à Orsay la semaine du 25 juin 2012. Il évoquait une contribution très importante des mathématiciens Pierre Deligne et Vladimir Drinfeld, à la géométrie arithmétique.

Rires dans la salle…

Qu’on ne s’y trompe pas, cette phrase de Rapoport est une boutade plaisante. Mais quand même: ne seraient-ils pas un peu nationalistes les mathématiciens français (et les autres) ? Voici quelques considérations badines à ce sujet.

Mais d’abord, quelques précautions : il n’est pas question d’aborder ici les choses de façon très sérieuse. Faute de compétences, nous n’allons pas discuter la difficile question du nationalisme et des mathématiques, ni celle de «qui a vraiment démontré quoi» en mathématiques. Toutes les attributions des énoncés mathématiques seraient, de toute manière, inexactes, d’après la loi de Stigler . Nous nous concentrerons sur le constat pratique suivant : quand nos collègues étrangers prennent un poste en France ⁴souvent attirés par le caractère permanent de ces postes., ils constatent parfois que ce qu’ils connaissent sous le nom de formule de Machin, s’appelle en France théorème de Bidule. Voici quelques exemples collectés auprès de collègues.

Connaissez-vous le triangle de Tartaglia ?

Avant d’en venir au triangle du titre, à tout seigneur, tout honneur, les théorèmes de Thalès et Pythagore. Si le nom théorème de Pythagore, semble universel, ce n’est pas le cas du théorème de Thalès (de Thalès de Milet), qui devient «Strahlensatz» en allemand, i.e. théorème des rayons et «intercept theorem». «Thalès theorem» désigne un tout autre énoncé en anglais.

Le triangle de ?

Quant au triangle de Tartaglia, c’est le nom italien du triangle de Pascal français, anglais, allemand, grec et russe.

Une compensation pour Tartaglia car il semble que c’est à Tartaglia que l’on doive attribuer les formules dites de Cardan qui permettent de résoudre l’équation polynomiale du 3e degré…

Le théorème d’existence et d’unicité de la solution d’une équation différentielle dit de Cauchy-Lipschitz, Cauchy un Français, Lipschitz, un Allemand, est à peu près partout ailleurs énoncé comme de Picard (un Français)-Lindelöf (un Finlandais). Notons sur cet exemple que même les Allemands utilisent cette dénomination, ce qui leur fait manquer l’occasion d’attribuer un théorème important à l’un de leurs compatriotes.

Le théorème de d’Alembert–Gauss, un Français et un Allemand, qui dit que tout polynôme à coefficients complexes s’annule dans le plan complexe, est plus souvent nommé théorème fondamental de l’algèbre dans les autres langues, même en allemand. En l’occurrence, l’énoncé du théorème revient à d’Alembert, ainsi qu’une démonstration fausse de cet énoncé, corrigée par Gauss.

Le théorème d’algèbre linéaire de Rouché-Fontené devient Kronecker-Capelli en Russie, Rouché-Capelli en Italie et dans les pays anglophones, Rouché-Frobenius en Espagne et dans les pays d’Amérique latine.

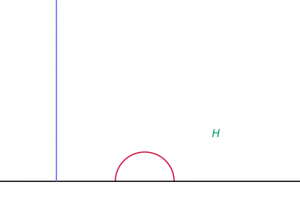
Le demi-plan de Poincaré

 

Venons-en maintenant à la Poincaré-mania soulignée par Rapoport. En français, la notion que Poincaré ⁵dont on célèbre en 2012 le centenaire de la disparition. Beaucoup de textes lui sont consacrés sur ce site, celui-ci par exemple. Signalons aussi cette vidéo .introduit dans «analysis situs» est devenue «groupe de Poincaré» et partout ailleurs, groupe fondamental, et est un objet tout à fait primordial en géométrie. Le demi-plan de Poincaré, en général noté H (H pour half-plane et non pas pour Henri Poincaré) est l’ensemble des nombres complexes de partie imaginaire strictement positive. Quoiqu’assez simple à définir, cet objet est immensément riche, que ce soit du point de vue arithmétique ou géométrique. Bref, ailleurs qu’en France, il est tout à fait logiquement appelé «demi-plan supérieur». Il est représenté sur la figure ci-dessus. L’axe horizontal ne fait pas partie de ce demi-plan. Le demi-cercle et la demi-droite verticale sont des courbes particulières de ce demi-plan ⁶des géodésiques pour la métrique définie sur le demi-plan de Poincaré..

Quant à la formule de Machin, au contraire du théorème de Bidule, elle existe bel et bien et permet de calculer les décimales de \(\pi\). \(\pi\), \(3,14\), \(14\) juillet. Place à la fête, aux feux d’artifice, et à l’étape du Tour de France du jour, où les Français tenteront de se distinguer.