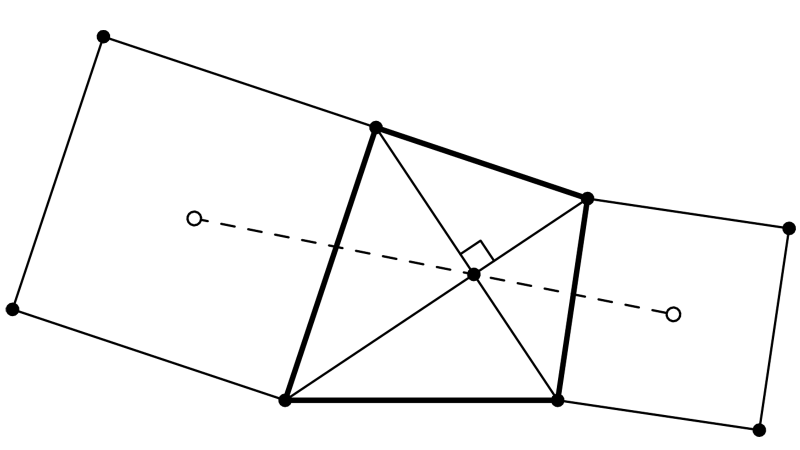
Problème "Fox and Holes" avec augmentation des possibilités du renard et du nombre d’observations.
Cette section est purement récréative, sans démonstration.
Nous vous proposons 5 problèmes, de simple à très complexe.


Problème "Fox and Holes" avec augmentation des possibilités du renard


Problème "Fox and Holes" avec augmentation des possibilités du renard et du nombre d’observations
.

.
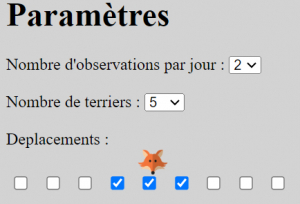
Un renard, Fox, est dans l’un de cinq terriers alignés.
Chaque nuit, Fox reste dans son terrier ou passe dans un terrier voisin de celui qu’il occupe.
Chaque jour, nous pouvons regarder dans deux des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox.
Ce problème est très facile.


Problème "Fox and Holes" avec augmentation des possibilités du renard et du nombre d’observations, un peu plus complexe
.

.
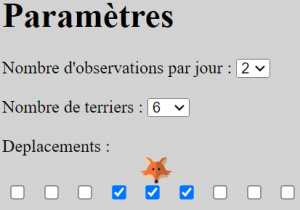
Un renard, Fox, est dans l’un de six terriers alignés.
Chaque nuit, Fox reste dans son terrier ou passe du terrier occupé à l’un des deux terriers parmi celui juste à gauche et celui juste à droite de celui juste à droite.
Chaque jour, nous pouvons regarder dans deux des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox.
Ce problème est assez facile.


Problème "Fox and Holes" avec augmentation des possibilités du renard et du nombre d’observations, encore un peu plus complexe
.

.
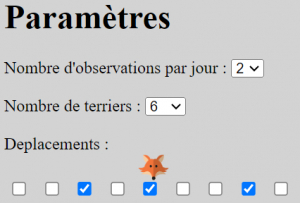
Un renard, Fox, est dans l’un de six terriers alignés.
Chaque nuit, Fox reste dans son terrier ou passe du terrier occupé à l’un des deux terriers parmi celui situé à 2 terriers vers la gauche et celui situé à 3 terriers vers la droite.
Chaque jour, nous pouvons regarder dans deux des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox.
Ce problème est un peu plus résistant que les deux précédents.


Problème "Fox and Holes" avec augmentation des possibilités du renard et du nombre d’observations, complexe
 .
.
Un renard, Fox, est dans l’un de sept terriers alignés.
Chaque nuit, Fox reste dans son terrier ou passe du terrier occupé à l’un des deux terriers parmi celui situé à 2 terriers vers la gauche et celui situé à 3 terriers vers la droite.
Chaque jour, nous pouvons regarder dans deux des terriers pour voir si Fox y est.
Donner une stratégie pour trouver Fox.
Ce problème est encore un peu plus résistant que les trois précédents.
Solution du cinquième défi
Rappel du défi

.
Un renard, Fox, est dans l’un de n terriers alignés.
Chaque nuit, Fox passe du terrier occupé à l’un des deux terriers parmi celui situé à g terriers vers la gauche et celui situé à d terriers vers la droite.
On suppose n ≥ g + d.
Chaque jour, nous pouvons regarder dans l’un des terriers pour voir si Fox y est. Donner une stratégie pour trouver Fox.
Remarque L’hypothèse n ≥ g + d garantit que de n’importe quel terrier, le renard a toujours au moins un déplacement possible.
Une modélisation adaptée
Il s’agit du cas le plus général quand le renard a deux possibilités de déplacement : les déplacements sont imposés de sens contraires, l’un vers la gauche et l’autre vers la droite, car s’ils allaient tous deux dans le même sens, au bout d’un moment, le renard n’aurait plus de déplacement à disposition.
Nous pouvons d’abord imposer, sans perte de généralité, que \(g\leq d\), quitte à changer l’ordre dans lequel on numérote les terriers (au lieu de numéroter de la gauche vers la droite, on numérote de la droite vers la gauche) et on inverse ainsi gauche et droite.
Nous allons ensuite supposer que \(g\) et \(d\) sont premiers entre eux (Voir plus bas Rappels sur l’identité de Bézout…). En effet, s’ils ne sont pas premiers entre eux, ils ont un PGCD égal à \(\delta\) qui est différent de \(1\) et à supposer que la position initiale du renard soit égale à \(\rho\) modulo \(\delta\), il ne va se déplacer que sur des terriers dont la position est égale à \(\rho\) modulo \(\delta\). Ainsi, on peut renuméroter les terriers sur lesquels il se déplace de la gauche vers la droite et considérer qu’avec cette nouvelle numérotation, le renard se déplace de \(\frac{g}{\delta}\) vers la gauche ou de \(\frac{d}{\delta}\) vers la droite. Selon la position initiale de Fox (c’est-à-dire de la valeur de \(\rho\)), c’est comme si nous avions \(\delta\) ensembles disjoints de terriers sur lesquels nous recherchons Fox successivement (d’abord pour \(\rho=0\), puis pour \(\rho=1\), … jusqu’à \(\rho=\delta-1\)).
Attention, ici il y a un peu de maths !
Légers rappels sur \(\mathbb{Z}/2\mathbb{Z}\) muni de la loi additive
Un nombre pair est de la forme \(2k\) avec \(k\in\mathbb{Z}\) et un nombre impair est de la forme \(2k+1\) avec \(k\in\mathbb{Z}\).
Ainsi : une somme de deux nombres pairs est \((2k)+(2k’)=2(k+k’)\) (avec \(k\in\mathbb{Z}\) et \(k’\in\mathbb{Z}\)) est paire ; une somme de deux nombres impairs est \((2k+1)+(2k’+1)=2(k+k’+1)\) (avec \(k\in\mathbb{Z}\) et \(k’\in\mathbb{Z}\)) est paire ; et une somme d’un nombre pair et d’un nombre impair est \((2k)+(2k’+1)=2(k+k’)+1\) (avec \(k\in\mathbb{Z}\) et \(k’\in\mathbb{Z}\)) est impaire.
En baptisant \(CL(0)\) l’ensemble des nombres pairs (ceux qui ont \(0\) pour reste dans la division euclidienne par 2) et \(CL(1)\) l’ensemble des nombres impairs (ceux qui ont \(1\) pour reste dans la division euclidienne par 2), on peut résumer la propriété précédente par :
\(CL(0)+CL(0)=CL(1)+CL(1)=CL(0)\)
et \(CL(0)+CL(1)=CL(1)+CL(0)=CL(1)\)
On peut aussi définir l’ensemble \(\mathbb{Z}/2\mathbb{Z}\) (ensemble des classes modulo 2) comme l’ensemble des \(CL(0)\) et \(CL(1)\) et lui donner la structure additive précédemment établie.
Quelques propriétés en vrac
\(CL(0)\) et \(CL(1)\) sont complémentaires dans \(\mathbb{Z}\) ;
\(\mathbb{Z}/2\mathbb{Z}\) muni de l’addition est un groupe commutatif avec \(CL(0)\) comme élément neutre ;
l’opposé de \(CL(1)\) est \(CL(1)\) (c’est cette propriété qui s’énonce « ‘retirer 1’ ou ‘ajouter 1’ sont confondues sur les classes modulo 2 ») ;
\(CL(0)\) n’est pas générateur de \(\mathbb{Z}/2\mathbb{Z}\) (car \(CL(1)\) n’est pas somme itérée de \(CL(0)\) puisque \(CL(0)+CL(0)+\ldots+CL(0)=CL(0)\)), mais \(CL(1)\) l’est (car \(CL(0)=CL(1)+CL(1)\) et \(CL(1)=CL(1)\), ce qui fait que tout élément de \(\mathbb{Z}/2\mathbb{Z}\) est engendré par une addition itérée de quelques \(CL(1)\)).
Rappels analogues sur \(\mathbb{Z}/3\mathbb{Z}\) muni de la loi additive
Un nombre multiple de \(3\) est de la forme \(3k\) avec \(k\in\mathbb{Z}\), un successeur d’un multiple de \(3\) est de la forme \(3k+1\) et un prédécesseur d’un multiple de \(3\) est de la forme \(3k+2\).
Comme précédemment, en baptisant \(CL(0)\) l’ensemble des nombres multiples de \(3\) (ceux qui ont \(0\) pour reste dans la division euclidienne par 3), \(CL(1)\) l’ensemble des nombres successeurs d’un multiple de \(3\) (ceux qui ont \(1\) pour reste dans la division euclidienne par 3) et \(CL(2)\) l’ensemble des nombres prédécesseurs d’un multiple de \(3\) (ceux qui ont \(2\) pour reste dans la division euclidienne par 3), on obtient :
\(CL(0)+CL(0)=CL(1)+CL(2)=CL(2)+CL(1)=CL(0)\)
\(CL(0)+CL(1)=CL(1)+CL(0)=CL(2)+CL(2)=CL(1)\)
et \(CL(0)+CL(2)=CL(1)+CL(1)=CL(2)+CL(0)=CL(2)\)
On peut aussi définir l’ensemble \(\mathbb{Z}/3\mathbb{Z}\) (ensemble des classes modulo 3) comme l’ensemble des \(CL(0)\), \(CL(1)\) et \(CL(2)\) et lui donner la structure additive précédemment établie.
Quelques propriétés en vrac
\(CL(0)\), \(CL(1)\) et \(CL(2)\) sont complémentaires dans \(\mathbb{Z}\) ;
\(\mathbb{Z}/3\mathbb{Z}\) muni de l’addition est un groupe commutatif avec \(CL(0)\) comme élément neutre ;
l’opposé de \(CL(1)\) est \(CL(2)\) (c’est cette propriété qui s’énonce « ‘retirer 1’ ou ‘ajouter 2’ sont confondues sur les classes modulo 3 »)
\(CL(0)\) n’est pas générateur de \(\mathbb{Z}/3\mathbb{Z}\) (car ni \(CL(1)\) ni \(CL(2)\) ne sont somme itérée de \(CL(0)\) puisque \(CL(0)+CL(0)+\ldots+CL(0)=CL(0)\)), mais \(CL(1)\) ou \(CL(2)\) l’est (car \(CL(0)=CL(1)+CL(1)+CL(1)=CL(2)+CL(2)+CL(2)\), \(CL(1)=CL(2)+CL(2)\) et \(CL(2)=CL(1)+CL(1)\), ce qui fait que tout élément de \(\mathbb{Z}/2\mathbb{Z}\) est engendré par une addition itérée de quelques \(CL(1)\) ou quelques \(CL(2)\)).
Retour au problème : « Qu’avons-nous appris des quelques exemples traités ? »
Ce qui est crucial dans les démonstrations des problèmes qui précèdent, c’est de regrouper correctement les cas.
Dans les problèmes où les déplacements sont de 1 vers la gauche ou de 1 vers la droite, on s’intéresse aux classes de nombres \(CL(0)\) des nombres pairs et \(CL(1)\) des nombres impairs. Sur ces classes de nombres, nous avons le diagramme suivant, que la flèche désigne « se déplacer dans le terrier voisin d’un côté » ou « de l’autre » (on dit que les opérations « retirer 1 » ou « ajouter 1 » sont confondues sur les classes modulo 2).
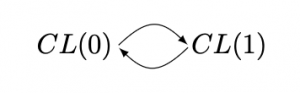
.
Dans les problèmes où les déplacements sont de 1 vers la gauche ou de 2 vers la droite, on s’intéresse aux classes de nombres \(CL(0)\) des nombres multiples de 3, \(CL(1)\) des nombres succédant aux multiples de 3 et \(CL(2)\) des nombres précédant les multiples de 3. Sur ces classes de nombres, nous avons le diagramme suivant, que la flèche désigne « se déplacer dans le terrier juste à gauche » ou « juste à droite de celui juste à droite » (on dit que les opérations « retirer 1 » ou « ajouter 2 » sont confondues sur les classes modulo 3).
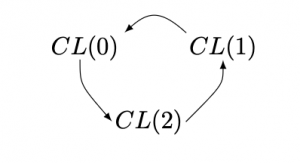
.
Rappels analogues sur \(\mathbb{Z}/(g+d)\mathbb{Z}\) muni de la loi additive
Un nombre multiple de \(g+d\) est de la forme \((g+d)k\) avec \(k\in\mathbb{Z}\), un successeur d’un multiple de \(g+d\) est de la forme \((g+d)k+1\), … et un prédécesseur d’un multiple de \(g+d\) est de la forme \((g+d)k-1\).
Comme précédemment, en baptisant \(CL(0)\) l’ensemble des nombres multiples de \(g+d\) (ceux qui ont \(0\) pour reste dans la division euclidienne par \(g+d\)), \(CL(1)\) l’ensemble des nombres successeurs d’un multiple de \(g+d\) (ceux qui ont \(1\) pour reste dans la division euclidienne par \(g+d\)), … et \(CL(g+d-1)\) l’ensemble des nombres prédécesseurs d’un multiple de \(g+d\) (ceux qui ont \(g+d-1\) pour reste dans la division euclidienne par \(g+d\)), on obtient :
\(CL(0)=CL(0)+CL(0)=CL(1)+CL(g+d-1)=CL(2)+CL(g+d-2)=\ldots=CL(g+d-1)+CL(1)\)
\(CL(1)=CL(0)+CL(1)=CL(1)+CL(0)=CL(2)+CL(g+d-1)=\ldots=CL(g+d-1)+CL(2)\)
\(\ldots\)
et \(CL(g+d-1)=CL(0)+CL(g+d-1)=CL(1)+CL(g+d-2)=\ldots=CL(g+d-1)+CL(0)\)
On peut aussi définir l’ensemble \(\mathbb{Z}/(g+d)\mathbb{Z}\) (ensemble des classes modulo \(g+d\)) comme l’ensemble des \(CL(0)\), \(CL(1)\), … et \(CL(g+d-1)\) et lui donner la structure additive précédemment établie.
Quelques propriétés en vrac
\(CL(0)\), \(CL(1)\), … et \(CL(g+d-1)\) sont complémentaires dans \(\mathbb{Z}\) ;
\(\mathbb{Z}/(g+d)\mathbb{Z}\) muni de l’addition est un groupe commutatif avec \(CL(0)\) comme élément neutre ;
l’opposé de \(CL(g)\) est \(CL(d)\) (c’est cette propriété qui s’énonce « ‘retirer \(g\)’ ou ‘ajouter \(d\)’ sont confondues sur les classes modulo \(g+d\) ») ;
\(CL(0)\) n’est pas générateur de \(\mathbb{Z}/(g+d)\mathbb{Z}\), mais \(CL(1)\) ou \(CL(g+d-1)\) l’est :
en effet, \begin{eqnarray*}
CL(i)&=&\underbrace{CL(1)+CL(1)+\ldots+CL(1)}_{i \mbox{ fois}}\\
&=&\underbrace{CL(g+d-1)+CL(g+d-1)+\ldots+CL(g+d-1)}_{g+d-i \mbox{ fois}},
\end{eqnarray*}
ce qui fait que tout élément de \(\mathbb{Z}/(g+d)\mathbb{Z}\) est engendré par une addition itérée de quelques \(CL(1)\) ou de quelques \(CL(g+d-1))\)).
Attention Tout élément distinct de \(CL(0)\) n’est pas forcément générateur : par exemple, si \(g=1\) et \(d=3\), \(CL(1)\) et \(CL(3)\) sont générateurs de \(\mathbb{Z}/4\mathbb{Z}\), mais pas \(CL(2)\).
Dans la section suivante, nous trouverons une condition pour que \(CL(i)\) (avec \(i\neq 0\)) soit générateur de \(\mathbb{Z}/(g+d)\mathbb{Z}\).
Rappels sur l’identité de Bézout et quelques conséquences dans la construction des classes modulo \(n\)
Nous définissons la notion de deux nombres premiers entre eux par l’identité de Bézout (nous aurions pu opter pour une définition autre qui dit que deux nombres sont premiers entre eux s’ils n’ont aucun facteur premier commun et cette définition est équivalente à la nôtre) : pour \(g\in\mathbb{Z}\) et \(d\in\mathbb{Z}\), \(g\) et \(d\) sont dits premiers entre eux si on peut trouver des entiers \(u\) et \(v\) tels que \[gu+dv=1.\]
Nous admettons avoir construit l’ensemble des classes modulo \(g+d\) \[\mathbb{Z}/(g+d)\mathbb{Z}=\{CL(0),CL(1), \ldots,CL(g+d-1)\},\] que nous avons muni de l’addition.
Si \(i\) et \(g+d\) sont premiers entre eux, alors \(CL(i)\) est un générateur de \(\mathbb{Z}/n\mathbb{Z}\), ce qui revient à dire que n’importe quel \(CL(j)\) peut être obtenue comme \(\displaystyle k\ CL(i)=\underbrace{CL(i)+CL(i)+\ldots+CL(i)}_{k\mbox{ fois}}\) pour un certain \(k\in\mathbb{Z}\).
Ceci peut se démontrer ainsi : si \(i\) et \(n\) sont premiers entre eux, alors on peut trouver des entiers \(u\) et \(v\) tels que \(iu+bn=1\) ; ce qui se traduit sur les classes modulo \(n\) par \(u\ CL(i)=CL(1)\) ; en multipliant par \(j\), on obtient alors \(ju\ CL(i)=jCL(1)=CL(j)\) ce qui est ce qu’il faut démontrer avec \(k=ju\).
La caractérisation des générateurs de \(\mathbb{Z}/(g+d)\mathbb{Z}\) est essentielle pour comprendre la stratégie générale déployée dans la section à suivre.
Définition d’une stratégie
Il existe toujours une stratégie pour trouver Fox. Nous pouvons même décrire complètement une stratégie dans le cas général. Cependant, nous choisissons de ne pas justifier cette stratégie car notre justification actuelle mobilise des propriétés des groupes additifs cycliques (idée qui est connectée aux diagrammes qui précèdent dans cette section) \(\mathbb{Z}/(g+d)\mathbb{Z}\) et ses éléments générateurs.
Grosso modo, la stratégie que nous proposons …
Premier temps
Soit \(k\) le plus grand entier naturel tel que \(g+kd < n\) est vraie.
On applique la stratégie « \(g+d\), \(g+2d\), \(g+3d\), …, \(g+kd\) ».
Ensuite, on calcule le reste \(r\) de la division euclidienne de \(k+1\) par \(g+d\) et on va agir différemment selon si \(CL(r)\) est ou n’est pas générateur de \(\mathbb{Z}/(g+d)\mathbb{Z}\) …
Premier cas :
si \(CL(r)\) est générateur de \(\mathbb{Z}/(g+d)\mathbb{Z}\), alors du deuxième au \((g+d)\)ème temps : on applique à nouveau la stratégie « \(g+d\), \(g+2d\), \(g+3d\), …, \(g+kd\) ».
Second cas :
si \(CL(r)\) n’est pas générateur de \(\mathbb{Z}/(g+d)\mathbb{Z}\), alors on cherche le plus petit \(\Delta\) tel que \(CL(r+\Delta)\) (ce \(\Delta\) existe toujours car \(CL(g+d-1)\) est toujours générateur) et du deuxième au \((g+d)\)ème temps, on applique \(\Delta\) observations farfelues « \(x_1\), \(x_2\), …, \(x_{\Delta}\) » avant de reprendre la stratégie « \(g+d\), \(g+2d\), \(g+3d\), …, \(g+kd\) ».
Explication de la stratégie précédente avec \(g=1\), \(d=2\) et \(n=7\)
Recherche de \(k\)
\(3\) (pour \(k=0\)) et \(5=3+2\) (pour \(k=1\)) sont les seules possibilités pour que \(g+kd < n\) soit vraie, on obtient \(k=1\) comme la plus grande des éventualités.
Dans le premier temps, on applique la stratégie « \(3, 5\) ».
Ensuite, on calcule \(r=2\) comme reste dans la division euclidienne de \(2=1+1\) par \(3\) et comme \(CL(2)\) est générateur de \(\mathbb{Z}/3\mathbb{Z}\) (voir dans les rappels en début de section 5), on entre dans le premier cas : dans les deuxième et troisième temps, on applique encore la stratégie « \(3, 5\) ».
Conclusion : la stratégie « \(3, 5, 3, 5, 3, 5\) » fonctionne comme c’est décrit à la fin de la solution du problème 4.
Explication de la stratégie précédente avec \(g=1\), \(d=2\) et \(n=8\)
Recherche de \(k\)
\(3\) (pour \(k=0\)), \(5=3+2\) (pour \(k=1\)) et \(7=3+2\times 2\) sont les seules possibilités pour que \(g+kd < n\) soit vraie, on obtient \(k=2\) comme la plus grande des éventualités.
Dans le premier temps, on applique la stratégie « \(3, 5, 7\) ».
Ensuite, on calcule \(r=0\) comme reste dans la division euclidienne de \(3=2+1\) par \(3\) et comme \(CL(0)\) n’est pas générateur de \(\mathbb{Z}/3\mathbb{Z}\) (voir dans les rappels en début de section 5), on entre dans le deuxième cas : on obtient \(\Delta=1\) car \(CL(1)\) est générateur de \(\mathbb{Z}/3\mathbb{Z}\) (voir dans les rappels en début de section 5) dans les deuxième et troisième temps, on applique la stratégie « \(x, 3, 5, 7\) » avec \(x\) une observation farfelue.
Conclusion : la stratégie « \(3, 5, 7, x, 3, 5, 7, x, 3, 5, 7\) » fonctionne comme c’est décrit à la fin de la section 4.
Retrouvez les autres défis et l'application
L’application
1e défi
2e défi
3e défi
4e défi
5e défi
Solution du dernier défi
Post-scriptum
La rédaction d’Images des maths, ainsi que les auteurs, remercient pour leur relecture attentive, les relecteurs dont le pseudonyme est le suivant -projetmbc, Walter et Gautier Dietrich.


 .
.