Ça n’en finira donc jamais ?

Détail1-infini (autour de 656 000)

Les concepts mathématiques utilisés par les artistes sont parfois bien élémentaires. Mais …

Lequel d’entre nous — au moins parmi ceux qui ont épousé la voie des mathématiques, quand à l’école primaire ils ont appris à compter — n’a éprouvé de l’étonnement et tenté d’imaginer la fin impossible de la liste des nombres entiers ? Personnellement je me souviens d’avoir été troublé de songer que je pourrais bien compter toute ma vie et aussi vite que je pourrais … que je n’en serais pas au bout. De quoi troubler mon esprit enfantin et lui donner à rêver.

Est-ce cette émotion là que l’artiste Roman Opalka voulut mettre à l’épreuve ? Lui affirme que c’était le temps qu’il voulait rendre visible.

Un jour, en l’année 1965 (à 34 ans), il décida de consacrer le reste de sa vie à compter et reporter sur la toile la suite infinie des nombres entiers. Quelle décision, quelle ascèse également ! car s’il est une chose de le dire … il en est une autre de s’y engager et surtout de s’y tenir. Certains seraient portés à prendre cela pour de la bêtise. Personnellement je trouve là une grande leçon de philosophie, d’humilité. Que sommes nous, quel est notre projet sur cette Terre où nous ne sommes que passagers ? Reconnaître et affirmer par cet acte minimum que nous ne sommes pas grand chose (compter c’est bien peu de chose) et que même cela nous ne le mènerons pas à terme. Faut-il être malade ou sage ?

En 1999, alors que je me sentais dans une impasse, je voulus adopter la même attitude et comme l’aventure des croissances était encore bien vive, je choisis de crayonner (au crayon fin) des carrés en progression de 3%. Je m’y suis tenu pendant 6 mois atteignant un carré de 2 x 2m environ … et puis j’ai renoncé. Ce n’était qu’une crise de dépression pourrais-je dire … On ne se jette pas dans une telle aventure par dépit. Il faut une force vive qui anime le projet.

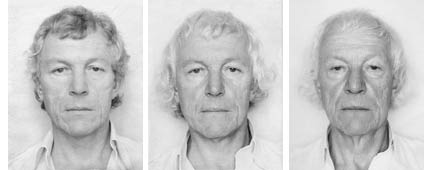
Pour apporter cependant quelque variété à son aventure, en 1972, ayant atteint le million, il décida d’ajouter une règle. À savoir que partant d’une toile noire avec écriture blanche, à chaque nouvelle toile il ajouterait un pour cent de blanc de plus dans le noir (chaque toile ayant le même format : 196 x 135cm). Ainsi de toile en toile les nombres finiraient par se dissoudre dans le fond. La deuxième était d’enregistrer sa voix énumérant les nombres qu’il écrirait. La troisième était de se prendre en photo (portrait de tête et de face sur fond blanc) à l’issue de chaque séance ²La deuxième et la troisième règle étaient déjà appliquées avant le million, il me semble … à vérifier … mais cela n’a pas grande importance.

Le résultat de ce contrat minimum est la production de véritables peintures … dont on pourrait oublier l’origine. On pourrait tout aussi bien n’y voir que des peintures décoratives ou bien des peintures à effet optique … car il faut s’approcher pour découvrir les nombres. Alors on remarque une certaine calligraphie des chiffres, … Comme généralement plusieurs toiles sont exposées on perçoit la progression du gris vers le blanc et la dissolution du tracé. Parallèlement aux toiles sont exposés les portraits montrant la progression avec l’âge des traits du visage et on entend cette voix (sa voix), telle une chanson monotone, énumérant la suite des nombres.

Cela fait donc maintenant des années que l’aventure a commencé. Je n’ai pas eu l’occasion de voir les dernières toiles. J’imagine qu’elles sont presque blanches et j’imagine la difficulté pour une personne âgée d’écrire en ne distinguant plus le fond … de la lettre (le chiffre).

Bien que la règle soit élémentaire, mathématiquement parlant, je trouve dans cette action et cet engagement beaucoup de liens avec l’engagement du chercheur. Humilité, persévérance, incertitude… ce n’est que lorsque un bon bout de chemin est accompli dans cette aventure qu’il est possible de se retourner et constater que le labeur opiniâtre produit un certain résultat. Résultat imaginable, entrevu ou pressenti par celui qui part ainsi à l’aventure … sinon il ne s’y risquerait pas. Mais résultat incertain quant à son intérêt ! En l’occurrence chez Opalka le résultat est visible, sensible et suscite l’émotion.

Si les nombres entiers sont sans fin … notre vie a un terme. Quel sera le dernier nombre tracé ?

Il paraît que la dernière toile est déjà achetée ???!!! Les collectionneurs sont vraiment bizarres … et je songe aux vautours dans les aventures de Lucky Luke !