
1er défi
Placer tous les chiffres de \(1\) à \(9\) de sorte que le nombre indiqué dans chaque région soit la somme des chiffres des cercles adjacents.
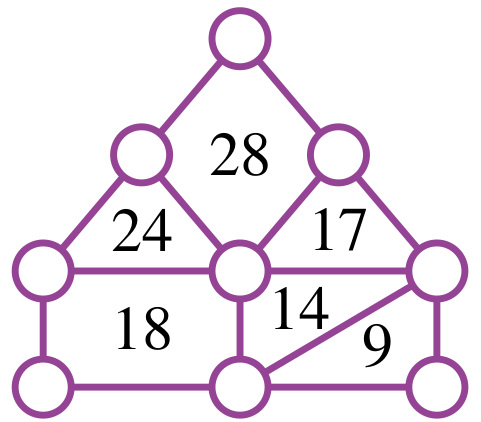
.


Solution du 1er défi
Dans le triangle de gauche, on doit avoir trois chiffres distincts dont la somme fait \(24\).
La seule possibilité est \(9+8+7\). Les quatre chiffres entourant le losange supérieur doivent avoir pour somme \(28\).
Les seules possibilités sont \(9+8+7+4\) et \(9+8+6+5\), mais comme l’un des trois chiffres parmi \(7\), \(8\) et \(9\) n’appartient pas à ce losange, la seule possibilité est \(9+8+6+5\), et \(7\) est donc le chiffre du sommet gauche du triangle de gauche.
On a donc la situation suivante~:
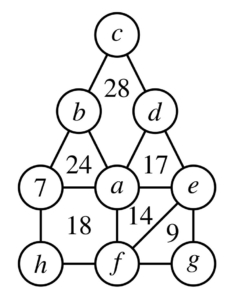
.
où les chiffres \(a\) et \(b\) sont \(8\) et \(9\) (pas nécessairement dans cet ordre), et \(c\) et \(d\) sont \(5\) et \(6\) (pas nécessairement dans cet ordre).
Supposons que \(a\) vaille \(9\). Alors,
\(h+f=18-7-9=2\), ce qui est impossible.
Donc \(a=8\) et \(b=9\).
Si \(d=6\), alors \(e=3\).
D’autre part, \(a+e+f = 14\) et donc \(f\) vaudrait \(3\), ce qui est impossible.
Par conséquent, \(d=5\) et \(c=6\).
Enfin, on obtient \(e=4\), \(f=2\), \(g=3\) et \(h=1\).
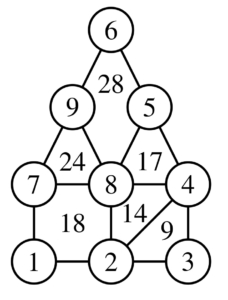
.
La seule possibilité est donc~:
2e défi
Dans une boutique de bière et de vin, il y a six fûts pleins qui contiennent \(15\), \(16\), \(18\), \(19\), \(20\) et \(31\) litres. Cinq d’entre eux sont remplis de vin et l’autre de bière. Le propriétaire décide de garder le fût de bière et vend le vin à deux clients différents. Si un des acheteurs a acheté le double de l’autre, quelle est la contenance du fût de bière ?


Solution du 2e défi
Réponse : Le fût de bière contient \(20\) litres
Notons \(y\) le nombre de litres de vin achetés par le client qui en a acheté le moins. Ainsi, l’autre a acheté \(2y\) litres de vin. Soit \(x\) le nombre de litres de bière.
On a donc: \(x+3y=15+16+18+19+20+31=119\).
Par conséquent, \(119-x\) doit être divisible par \(3\).
Comme \(119=3 \times 39 +2\), cela signifie que la division euclidienne de \(x\) par \(3\) laisse \(2\) comme reste. Le seul nombre parmi \(15\), \(16\),
\(18\), \(19\), \(20\) et \(31\) qui ait cette propriété est \(20\).
Par conséquent, le fût de bière est celui qui contient \(20\) litres.
De plus, un client a acheté \(33=15+18\) litres de vin et l’autre \(66=16+19+31\) litres.
3e défi
Placer huit entiers distincts entre \(0\) et \(12\) (inclus) sur les sommets d’un cube de telle sorte que si l’on associe à chaque arête la différence des deux nombres placés à ses extrémités, on obtienne tous les nombres entre \(1\) et \(12\).


Solution du 3e défi
Réponse :
Comme \(12\) est une des différences, les nombres \(0\) et \(12\) doivent être placés sur deux sommets adjacents du cube.
Comme \(11\) est une autre différence, soit \(1\) est placé sur un sommet adjacent au sommet contenant le nombre \(12\), soit \(11\) est placé sur un sommet adjacent au sommet contenant \(0\).
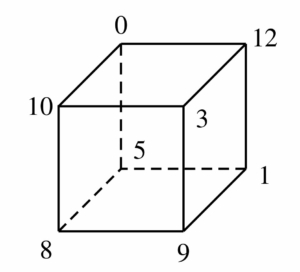
.
Supposons que le sommet \(1\) soit sur un sommet adjacent au sommet étiqueté par \(12\). Alors, une possibilité est la suivante :
4e défi
Trouver cinq entiers strictement positifs consécutifs ayant la propriété suivante : la somme des carrés des deux plus grands nombres est égale à la somme des carrés des trois autres nombres.


Solution du 4e défi
Réponse : \(10\), \(11\), \(12\), \(13\) et \(14\).
Notons \(x-2\), \(x-1\), \(x\), \(x+1\) et \(x+2\) les cinq entiers naturels consécutifs.
Alors la condition cherchée est équivalente aux équations suivantes~:
\[
\begin{eqnarray*}
(x+1)^2+(x+2)^2 &=& x^2+(x-1)^2+(x-2)^2\\
x^2+2x+1+x^2+4x+4 &=& x^2+x^2-2x+1+x^2-4x+4\\
x^2-12x &=& 0\\
x(x-12) &=& 0.
\end{eqnarray*}
\]
Donc \(x = 0\) ou \(x = 12\).
Comme les entiers doivent être strictement positifs, la seule solution est \(x = 12\).
Par conséquent, les nombres sont: \(10\), \(11\), \(12\), \(13\) et \(14\).
5e défi

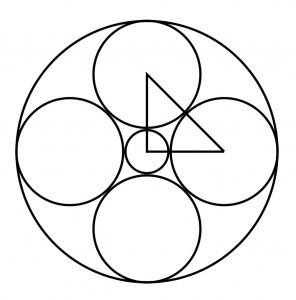
.
Quatre cercles de même rayon sont tangents entre eux et à deux cercles concentriques. Le petit cercle a un rayon de \(1\)cm. Quel est le rayon du plus grand cercle ?


Solution du 5e défi
Réponse : \(3+2\sqrt{2}\,\textrm{cm}\)
.
On considère le triangle rectangle de la figure ci-dessous, dont les sommets sont les centres de trois cercles. On appelle \(x\) le rayon des quatre cercles identiques.
En appliquant le théorème de Pythagore, on obtient~:
\[\begin{eqnarray*}
2(1+x)^2&=&(2x)^2\\
2x^2-4x-2 &=& 0\\
x^2-2x-1 &=&0
\end{eqnarray*}\]
Donc, on a \(x = 1\pm \sqrt{2}\).
Comme \(x\) est positif, on trouve \(x= 1+\sqrt{2}\,\textrm{cm}\).
Par conséquent, le rayon du plus grand cercle est \(1+2(1+\sqrt{2})=3+2\sqrt{2}\,\textrm{cm}\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


14h44
1er défi
\(9+8+7=24\) et \(4+3+2=9\).
J’ai décidé de remplir le triangle du \(9\).
En tâtonnant un peu et grâce aux présences du \(18\) et du \(14\), j’ai rapidement trouvé à placer le \(2\) en bas au milieu, le \(3\) en bas à droite et le \(4\) au dessus de \(3\).
Ensuite, tout s’enclenche.
La clé, donc : remplir les chiffres autour du \(9\).
\(0\) \(0\) \(6\) \(0\) \(0\)
\(0\) \(9\) \(0\) \(5\) \(0\)
\(7\) \(0\) \(8\) \(0\) \(4\)
\(1\) \(0\) \(2\) \(0\) \(3\)
9h21
2e défi
La quantité de vin est un multiple de 3.
La quantité initiale de boissons est :
\((15+ 16+ 18+ 19+ 20+ 31) \% 3 = 2\)
Le caviste garde donc un fût de capacité \(x\) tel que \(x \% 3 = 2\). La seule valeur \(x= 20\).
Le fût bière est donc celui de 20.
Pour la suite :
\(15+ 16+ 18+ 19+ 31 = 99\)
Donc un client reçoit 33 et l’autre 66. Seule possibilité \(15 + 18\) et \(16 + 19 + 31\)
22h17
2e défi
Il y a 6 combinaisons de 5 chiffres parmi 6.
La bonne combinaison est celle dont la somme de ses chiffres est un multiple de 3.
En effet soit a et b les 2 acheteurs de vins.
On b=2a, donc a +2a=3a.
La seule combinaison qui soit multiple de 3 est : 15+16+18+19+31= 99
Reste donc 20 qui est la contenance du fût de bière.
9h20
3e défi
Bonjour
On peut mettre sur la face supérieure
11 3
0 12
(on a les différences 8, 9, 11 et 12)
et au-dessous sur la face inférieure
4 6
10 5
(on a les différences 2, 1, 5 et 6)
et pour les arêtes verticales, on a les différences
7 3
10 8
14h09
Rphino
On peut mettre sur la face supérieure
11 3
0 12
(on a les différences 8, 9, 11 et 12)
et au-dessous sur la face inférieure
8 9
10 5
10h31
4e défi
Les deux plus grands nombres sont consécutifs, donc de parité opposée. La somme de leurs carrés est alors impaire, et ainsi Il y a un seul nombre impair parmi les trois autres, et c’est forcément le deuxième. On cherche donc \(n>0\) tel que \[(2n)^2 + (2n+1)^2 + (2n+2)^2 = (2n+1)^3 + (2n+1)^4\]
Après simplification on obtient \(n^2 -4n -5 = 0\), dont la seule solution positive est \(n=5\), ce qui donne les nombres \(10,11,12,13,14\), et en effet on peut vérifier que \(10^2 + 11^2 + 12^2 = 365 = 13^2 + 14^2\)
10h34
Oups ! Erreur de copier coller 🙂
\[(2n)^2+(2n+1)^2+(2n+2)^2=(2n+3)^2+(2n+4)^2\]
19h06
4e défi
Afin de tenter de calculer facilement le trinôme du 2nd degré, je prends \(x-1\), \(x\) et \(x+1\) pour les trois plus petits entiers ce qui donne rapidement \(3x^2+2\) pour la somme de leurs carrés ; je calcule pas trop difficilement pour les deux entiers les plus grands une somme de carré égale à \(2x^2+10x+13\).
Alors \(x^2-10x-11=0\) a pour solution \(x=11\).
Les cinq entiers sont donc \(10\), \(11\), \(12\), \(13\) et \(14\).
23h36
4e défi
n²+(n+1)²+(n+2)²=(n+3)²+(n+4)²
— > n²-8n-20=0
n=10
Les 5 nombres : 10, 11, 12 ,13, 14
8h54
4e défi
Il me semble que le plus simple est de prendre n-2, n-1, n, n+1 et n+2..
Après développements et simplification on obtient n² = 12n soit n = 12
( n = 0 conduisant à la solution triviale mais interdite ici -2, -1, 0, 1 et 2
9h24
Ah oui !
Définitivement la plus simple puisque pas de trinôme !
Bravo pour le coup d’œil 🙂 !!!
10h31
5e défi
Soit \(R\) le rayon du grand cercle et \(r\) celui des cercles moyens. On a \(R=2r+1\). De plus en appliquant le théorème de Pythagore au triangle rectangle isocèle formé par le centre du petit cercle et deux centres de cercles moyens tangents entre eux, on obtient \(2(1+r)^2=4r^2\) d’où en résolvant \(r=1+\sqrt(2)\) et finalement \(R=2\sqrt(2)+3\).
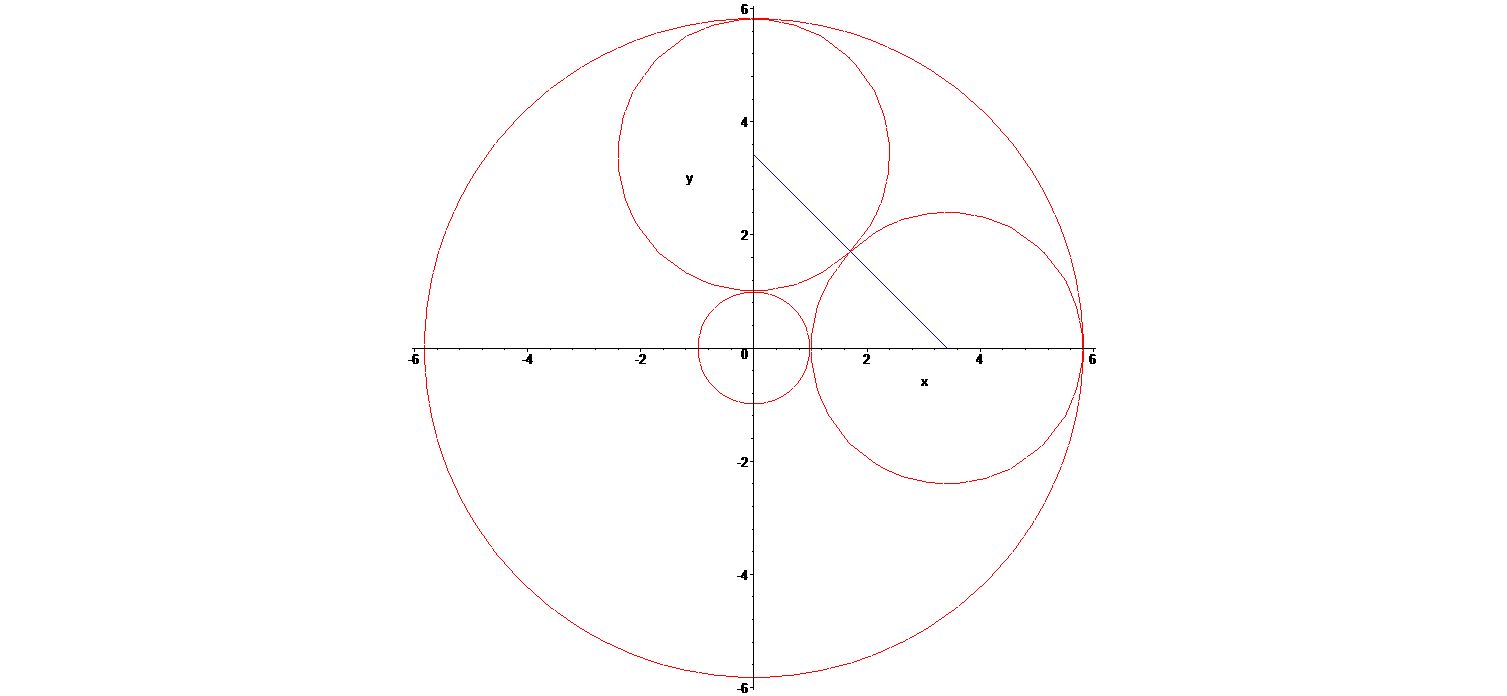
14h01
5e défi
2(1+r)²=4r² —> r=1+√3
Et R=2√3+ 3
15h12
\(2(1+r)^2=4r^2\) on développe et simplifie \(r^2-2r-1=0\), puis \((r-1)^2=2\) et \(r=1\pm \sqrt2\)
8h13
Oups ? Effectivement