Premier défi : le problème du mois
Dans la figure suivante, chaque nombre indique le périmètre en cm du rectangle qui l’entoure. Déterminer le périmètre du grand rectangle.
.
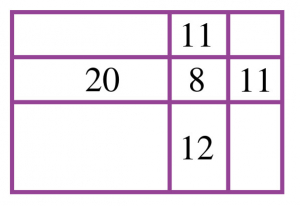
Solution du premier défi
Notons \(x\), \(y\), \(z\) et \(w\) les longueurs en cm des segments, comme sur la figure ci-dessous.
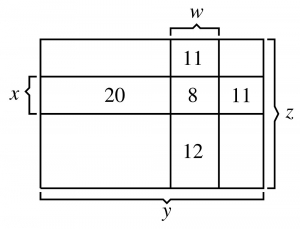
On a alors \( 8=2(x+w) \). De \[2(z+w) = 11+8+12-4w = 31-4w,\] on obtient \( 2z+6w=31 \). De même, \[ 2(x+y) = 20+8+11-4x\] implique \(2y+6x=39\). Le périmètre du grand rectangle est donc \[2(y+z)=2z+6w+2y+6x-6(x+w)=31+39-3\times 8=46\,{\rm cm}\].
Deuxième défi
Placer les nombres de \(1\) à \(9\) dans ce carré de telle sorte que les sommes de chaque colonne, chaque ligne et chaque diagonale soient deux à deux distinctes.
.
Solution du deuxième défi
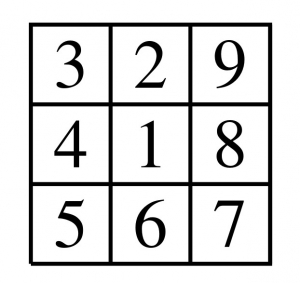
Une des solutions possibles est la suivante
Troisième défi
La police a appréhendé trois suspects d’un vol. On sait que l’un d’eux dit la vérité, un autre ment et le troisième dit une information vraie et une fausse. \(A\) dit : « Je ne suis pas un voleur, et \(C\) est le voleur. » \(B\) dit : « \(C\) est innocent et \(A\) est un voleur. » \(C\) dit : « Je ne suis pas un voleur et \(B\) est innocent. » Un seul d’entre eux est un voleur. Lequel?
Solution du troisième défi
Supposons tout d’abord que \(C\) dit la vérité. Alors le voleur est nécessairement \(A\). Mais dans ce cas, \(B\) a dit la vérité aussi, ce qui est impossible. Supposons maintenant que \(B\) dit la vérité. Alors \(A\) est le voleur, et donc les deux affirmations de \(C\) sont aussi vraies, ce qui est impossible. C’est donc \(A\) qui dit la vérité, à savoir que \(C\) est le voleur. Dans ce cas, les deux affirmations de \(B\) sont fausses, tandis que \(C\) ment sur une et dit la vérité sur l’autre.
Quatrième défi
Trouver un nombre entier \(r\) à trois chiffres dont les trois chiffres sont égaux et tel que \(r=1+2+\ldots+n\) pour un certain entier \(n\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
8h56
Premier défi
Le grand rectangle est composé de \(4 * 3 = 12\) segments. Si on additionne les périmètres des \(4\) rectangles entourant le rectangle central, on compte une fois chacun de ces \(12\) segments, plus une fois chaque côté du rectangle central. Donc le périmètre du grand rectangle est \(11 + 20 + 12 + 11 – 8 = 46\).
8h32
Deuxième défi
Une des solutions est de placer 1 au centre puis les autres chiffres par ordre croissant en tournant autour de 1.
5 4 3
6 1 2
7 8 9
Les sommes obtenues sont 11 et 15 sur les diagonales, 12, 9, 24 sur les lignes, et 18, 13, 14 sur les colonnes.
21h22
Je trouve 71 solutions avec une première ligne 1 2 3
N° Solution les 8 sommes toutes distinctes
0000 : 123 458 697 6 17 22 11 16 18 13 14
0001 : 123 459 687 6 18 21 11 15 19 13 14
0002 : 123 459 768 6 18 21 12 13 20 14 15
0003 : 123 485 796 6 17 22 12 19 14 15 18
0004 : 123 468 579 6 18 21 10 15 20 16 14
0005 : 123 478 596 6 19 20 10 18 17 14 15
0006 : 123 479 586 6 20 19 10 17 18 14 15
0007 : 123 489 657 6 21 18 11 15 19 16 17
0008 : 123 467 985 6 17 22 14 16 15 12 18
0009 : 123 498 765 6 21 18 12 17 16 15 19
0010 : 123 945 687 6 18 21 16 14 15 12 13
0011 : 123 945 768 6 18 21 17 12 16 13 14
0012 : 123 845 976 6 17 22 18 13 14 11 16
0013 : 123 748 596 6 19 20 13 15 17 11 12
0014 : 123 749 586 6 20 19 13 14 18 11 12
0015 : 123 847 596 6 19 20 14 15 16 11 12
0016 : 123 947 586 6 20 19 15 14 16 11 12
0017 : 123 948 576 6 21 18 15 13 17 11 12
0018 : 123 746 859 6 17 22 16 11 18 14 15
0019 : 123 946 857 6 19 20 18 11 16 12 15
0020 : 123 849 657 6 21 18 15 11 19 12 13
0021 : 123 946 875 6 19 20 18 13 14 10 15
0022 : 123 748 695 6 19 20 14 15 16 10 13
0023 : 123 947 685 6 20 19 16 14 15 10 13
0024 : 123 749 865 6 20 19 16 12 17 10 15
0025 : 123 847 965 6 19 20 18 12 15 10 16
0026 : 123 849 765 6 21 18 16 12 17 10 14
0027 : 123 948 765 6 21 18 17 12 16 10 14
0028 : 123 574 986 6 16 23 15 17 13 14 19
0029 : 123 784 659 6 19 20 14 15 16 18 17
0030 : 123 684 975 6 18 21 16 17 12 14 20
0031 : 123 874 695 6 19 20 15 18 12 13 16
0032 : 123 894 765 6 21 18 16 17 12 15 19
0033 : 123 568 497 6 19 20 10 17 18 14 13
0034 : 123 579 468 6 21 18 10 15 20 16 14
0035 : 123 658 497 6 19 20 11 16 18 13 12
0036 : 123 856 479 6 19 20 13 14 18 15 12
0037 : 123 956 487 6 20 19 14 15 16 13 12
0038 : 123 765 498 6 18 21 12 17 16 15 13
0039 : 123 785 469 6 20 19 12 16 17 18 15
0040 : 123 967 485 6 22 17 14 16 15 12 13
0041 : 123 796 485 6 22 17 12 19 14 15 16
0042 : 123 567 849 6 18 21 14 12 19 16 17
0043 : 123 576 948 6 18 21 15 13 17 16 19
0044 : 123 658 947 6 19 20 16 11 18 13 17
0045 : 123 856 947 6 19 20 18 11 16 13 17
0046 : 123 859 647 6 22 17 15 11 19 13 14
0047 : 123 958 647 6 22 17 16 11 18 13 14
0048 : 123 857 946 6 20 19 18 11 16 12 17
0049 : 123 859 746 6 22 17 16 11 18 12 15
0050 : 123 965 847 6 20 19 18 12 15 14 17
0051 : 123 678 549 6 21 18 12 13 20 17 15
0052 : 123 679 548 6 22 17 12 13 20 16 15
0053 : 123 768 549 6 21 18 13 12 20 16 14
0054 : 123 769 548 6 22 17 13 12 20 15 14
0055 : 123 568 794 6 19 20 13 17 15 11 16
0056 : 123 569 874 6 20 19 14 15 16 11 17
0057 : 123 576 984 6 18 21 15 17 13 12 19
0058 : 123 657 984 6 18 21 16 15 14 10 17
0059 : 123 658 974 6 19 20 16 14 15 10 17
0060 : 123 856 974 6 19 20 18 14 13 10 17
0061 : 123 956 874 6 20 19 18 14 13 10 16
0062 : 123 857 964 6 20 19 18 13 14 10 17
0063 : 123 965 874 6 20 19 18 15 12 11 17
0064 : 123 795 864 6 21 18 16 17 12 14 20
0065 : 123 687 594 6 21 18 12 19 14 13 16
0066 : 123 698 574 6 23 16 12 18 15 14 17
0067 : 123 768 594 6 21 18 13 17 15 11 14
0068 : 123 678 954 6 21 18 16 14 15 12 19
0069 : 123 679 854 6 22 17 15 14 16 12 18
0070 : 123 687 954 6 21 18 16 15 14 13 20
13h53
Présentons sous forme de tableau les déclarations faites, avec ‘I’ pour innocent, ‘V’ pour voleur, et ‘.’ information manquante :
A I . V
B V . I
C . I I
A B C
En supposant ces déclarations cohérentes, c’est à dire que chacune désigne un seul voleur, alors on peut facilement compléter ce tableau ainsi :
A I I V
B V I I
C V I I
A B C
B et C font la même déclaration. Il est impossible que l’un d’eux dise la vérité, car la déclaration de l’autre devrait être différente au moins sur un point, car un seul entre tous dit la vérité.
Par conséquent A dit la vérité et C est le voleur.
Pour être complet, les deux déclarations de C (cf premier tableau) qui sont en contradiction avec A et la première déclaration de C sont fausses, mais la deuxième déclaration de C, qui innocente B est vraie.
17h07
Troisième défi
Je devais écrire : « Pour être complet, les deux déclarations de B », au dernier paragraphe.
16h10
Quatrième défi
Soit \(c\) le chiffre répété trois fois. Alors \(r = 111c = 1 + … + n \).
\( 37*3c = n(n+1)/2 \)
\( 37*6c = n(n+1) \)
Or \( n \) et \( n+1 \) sont premiers entre eux, et \( 37 \) est premier, donc \( 37 \) divise \( n \) ou \( n+1 \).
Si \( n \) et \( n+1 \) étaient différents de \( 37 \), alors on aurait \( n+1 \geq 37*2 = 74\), d’où \( r \geq 73*74/2 = 2701\), et ainsi \( r \) aurait au moins quatre chiffres.
Donc \( n = 37 \) ou \( n = 36\).
Pour \( n = 37 \) on obtient \( r = 37*38/2 = 703\) qui ne convient pas.
Pour \( n = 36 \) on obtient \( r = 36*37/2 = 666\) qui est donc la seule solution.
14h00
Par définition, on a:
n(n+1)/2=r
Soit n²+n-2r=0
Avec le discriminant de cette équation qui doit être un entier:
√(1+8r) entier.
Parmi les 9 possibilités pour r (111, 222…888, 999),
Seul r=666 donne
√(1+8×666)=73 entier