Inversion dans le plan

Pour multiplier de très grands nombres, à l’époque où les calculatrices n’existaient pas, on utilisait les logarithmes. Le simple fait que les logarithmes transforment les produits en additions et les puissances en produits facilite grandement le travail. Si nous devons trouver le produit de deux très grands nombres, il nous suffit de trouver leurs logarithmes, de les additionner et de trouver à quel nombre correspond ce logarithme.

Ce que nous avons fait, c’est transformer notre problème en un autre plus simple, le résoudre et appliquer la transformation inverse à la solution, obtenant ainsi la solution du problème original. Ces types de problèmes sont communément appelés problèmes inverses.

L’image montre l’application d’une technique célèbre connue sous le nom d’inversion⁵Soit \(P\) et \(P’\) deux points colinéaires de centre \(O\) d’un cercle de rayon \(r > 0\). Si

\begin{equation}
OP\cdot OP’=r^2,
\end{equation}

alors chacun des points \(P\) et \(P’\) est dit être l’inverse de l’autre par rapport au cercle. Comprendre la relation ci-dessus comme signifiant que \(OP\) et \(OP’\) sont des segments dirigés, et donc que \(P\) et \(P’\) se trouvent du même côté du centre. Le point \(O\) est appelé centre d’inversion, le cercle est appelé cercle d’inversion et son rayon est appelé rayon d’inversion. Dans cette relation, il y a symétrie: si \(P’\) est l’inverse de \(P\), alors \(P\) est l’inverse de \(P’\). On dit alors que les points \(P\) et \(P’\) sont des points inverses par rapport au cercle.

De la même manière, toute courbe peut être transformée en une autre courbe et on a des courbes inverses. Cette technique de transformation par rapport à un cercle est appelée inversion. qui permet de transformer des courbes de manière conforme en d’autres courbes. Cette méthode consiste à utiliser une transformation conforme de seconde espèce (ou isogonale ⁶Une transformation isogonale est une carte qui préserve les amplitudes des angles locaux, mais pas leur orientation.) du plan qui préserve les angles entre les courbes mais pas leur orientation. Les lignes qui ne passent pas par le centre d’inversion sont transformées en cercles qui y passent, et vice versa. Une façon différente de prouver le deuxième théorème de Thalès⁷Le deuxième théorème de Thalès affirme que l’angle inscrit dans un demi-cercle est un angle droit., simple, ou le porisme de Steiner⁸Considérons deux cercles non concentriques, l’un à l’intérieur de l’autre. Nous commençons par inscrire un cercle entre les deux, puis nous inscrivons des cercles tangents aux deux cercles donnés et au dernier. Il arrivera un moment où le cercle que nous inscrivons chevauche le premier, ou lui est tangent. Le porisme de Steiner affirme que cela ne dépend pas de la position du premier cercle inscrit., difficile, est d’utiliser cette transformation.

Il convient de mentionner que de nombreux problèmes des Olympiades internationales de mathématiques (IMO) peuvent être résolus avec de belles démonstrations en utilisant cette transformation.

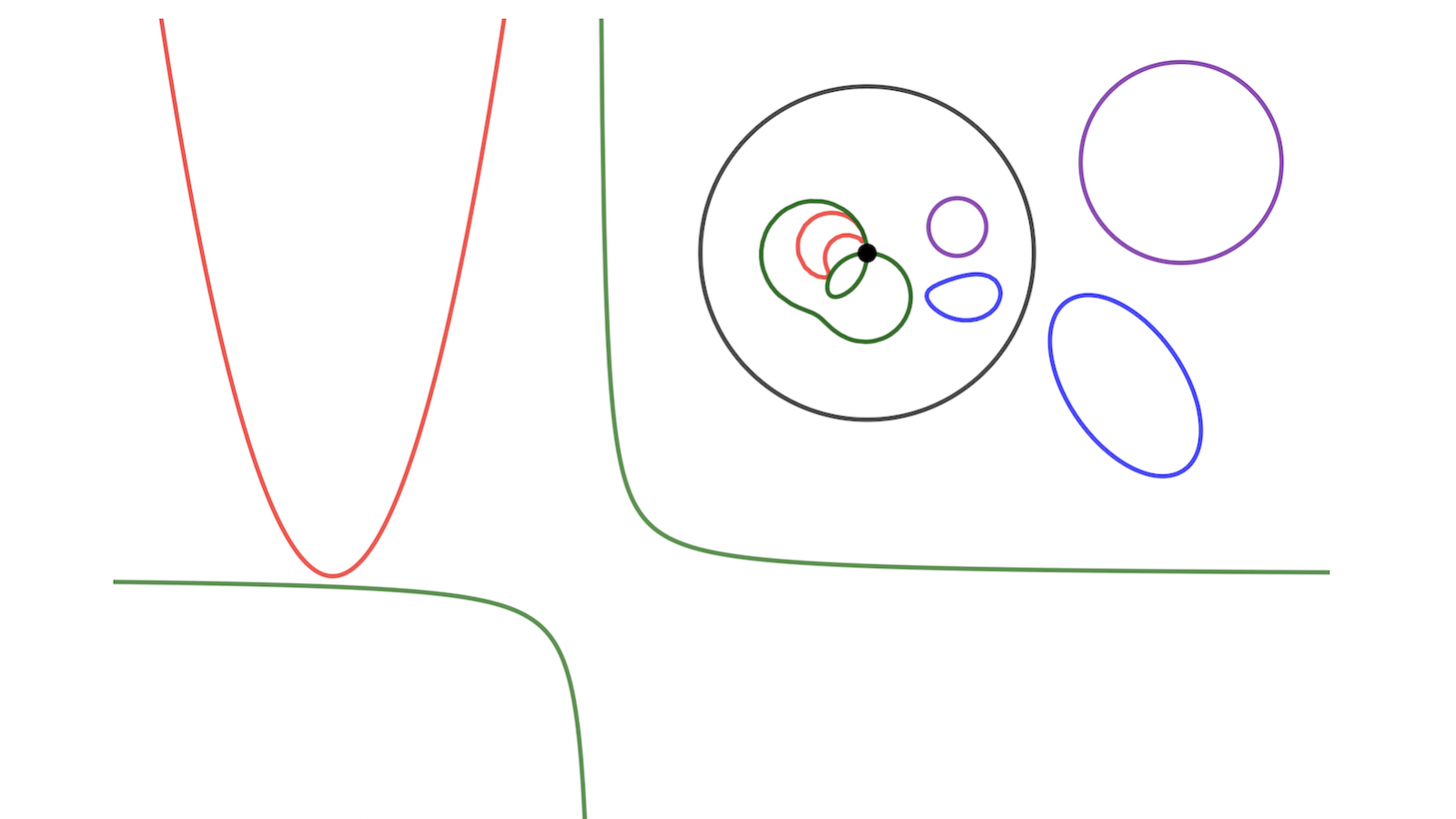
L’image montre les coniques du second degré avec leurs courbes inverses respectives par le cercle d’inversion noir.