Figure sans paroles #8.1.17

Commentaires

1. Sidonie

   juin 26, 2023
   19h05

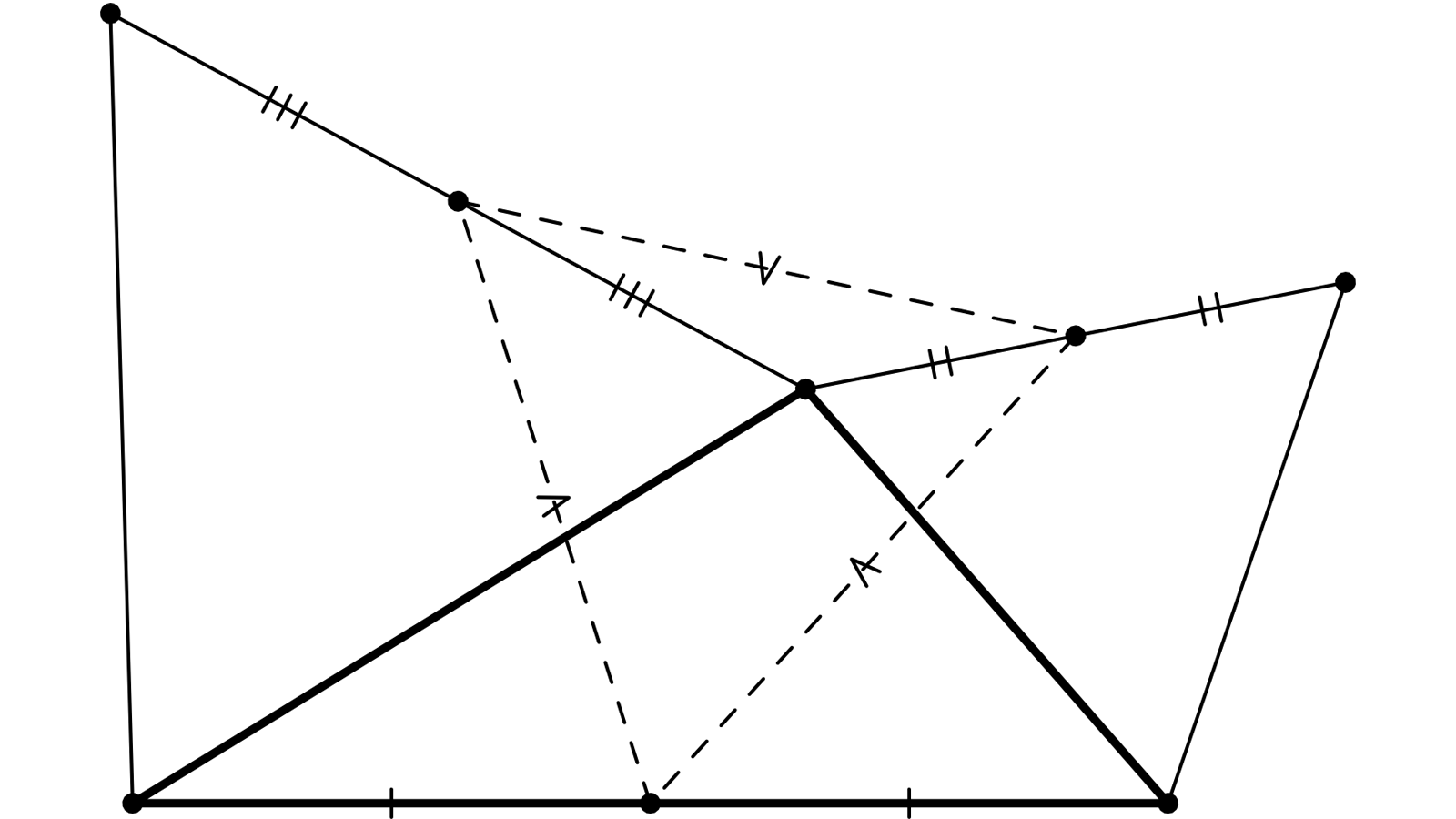
   ADB et ACE sont équilatéraux. F, G et H sont les milieux de [AD], [BC] et [AE] .
   Ce qui ferait de FGH un autre équilatéral : nous l’allons prouver tout à l’heure.
   I est tel que DIE est équilatéral.
   La rotation de centre D et d’angle 60° transforme B en A et I en E donc BI = AE = AC
   La rotation de centre E et d’angle 60° transforme A en C et D en I donc CI = AD = AB
   Le quadrilatère ABIC ayant des côtés opposés égaux est donc un parallélogramme et G milieu de la diagonale BC est aussi le milieu de l’autre diagonale AI
   L’homothétie de centre A et de rapport 0,5 transforme l‘équilatéral DIE en FGH à son tour équilatéral.

   

   Connectez-vous pour répondre
• Reine

  juin 27, 2023
  15h04

  Cette propriété peut aussi se voir comme un cas particulier d’un phénomène plus général : Étant donné dans le plan cinq points A, B, C, D et E tels que les triangles DBA et ACE soient directement semblables [1], le triangle FGH ayant pour sommets les milieux de AD, BC et AE est directement semblable aux deux précédents. En reprenant votre argument d’homothétie, il suffit de le montrer pour le triangle DIE, où I est le point faisant de BACI un parallélogramme.

  Effectuons successivement deux transformations du plan : d’abord la translation qui envoie B sur A, puis la similitude directe S de centre A envoyant C sur E. [2] La composée de ces deux opérations est une certaine similitude directe S’, de même rapport et de même angle que S.

  Puisque S’(B) = A, S’ est l’unique similitude directe envoyant B sur A et de mêmes rapport et angle que S. Mais la similitude de centre D ayant ce rapport et cet angle envoie elle aussi B sur A, car DBA est semblable à ACE ; ainsi, le centre de S’ n’est autre que D.

  Et comme S’ envoie I sur E (via C), le triangle DIE est directement semblable à DBA, ce qu’il fallait établir.

  [1] Égalité de leurs angles orientés.

  Connectez-vous pour répondre