Figure sans paroles #8.1.18

Commentaires

1. Reine

   juillet 9, 2023
   10h02

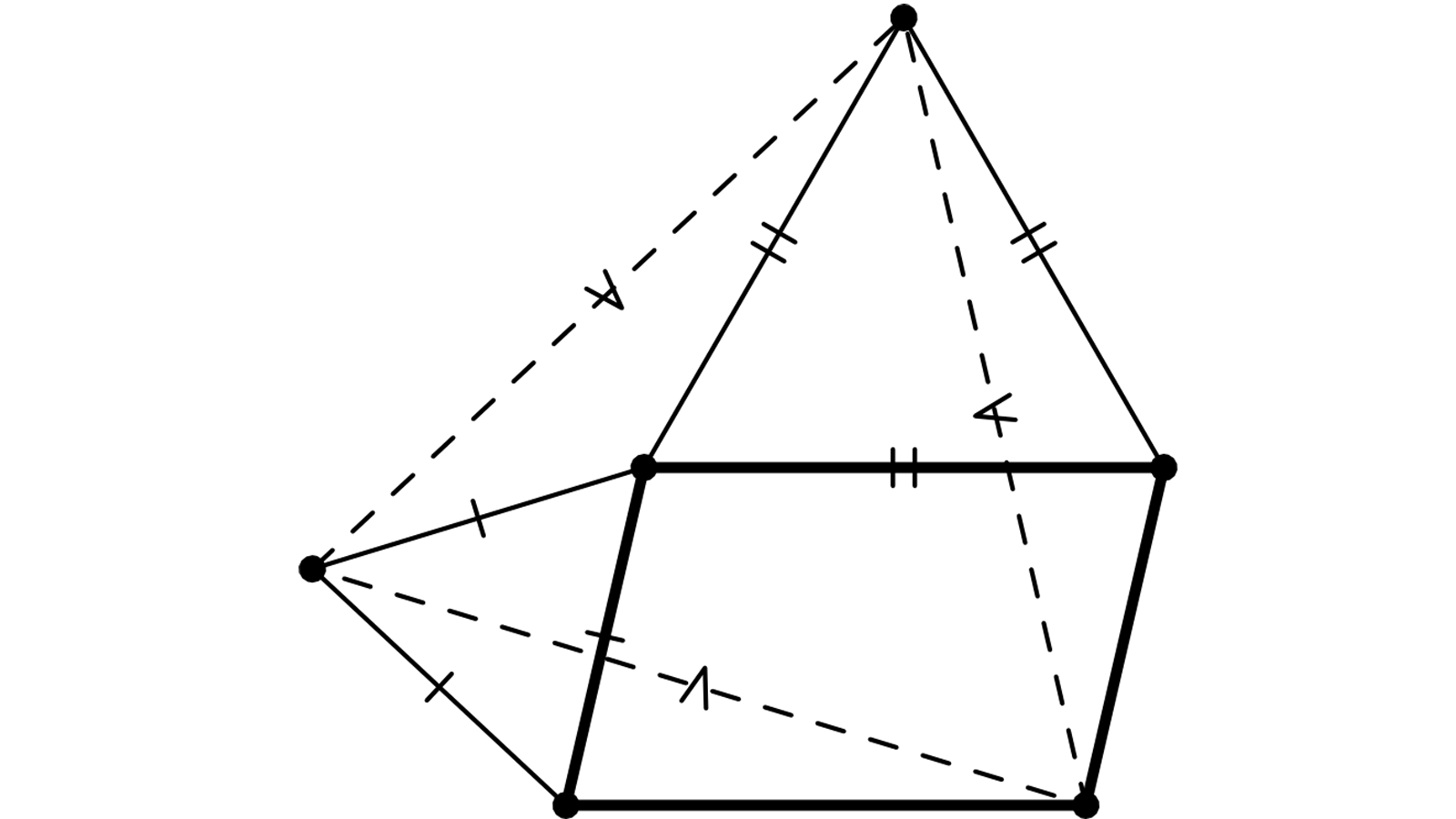
   Cette figure m’intrigue. Partant d’un parallélogramme et de deux triangles équilatéraux (en traits pleins), on en voit apparaître un troisième (en pointillés). Par un argument immédiat d’homothétie, cette propriété équivaut à celle présentée, la semaine dernière, par la Figure sans Paroles 8.1.17. Deux démonstrations différentes, fort simples, en avaient été proposées, toutes deux utilisant cette homothétie. Mais si le site nous a proposé 8.1.17 avant la figure 8.1.18 ci-dessus, c’est sans doute que 8.1.17 pouvait être établie par un argument encore plus simple, évitant l’homothétie. Lequel ?

   Connectez-vous pour répondre
2. Hébu

   juillet 10, 2023
   21h05

   cette hypothèse serait fondée sur l’idée d’une « progression » dans la complexité (mot pris ici comme le contraire de simplicité).

   Mais, je rédige ceci la semaine qui suit, après avoir vu la figure suivante (8.1.19) — encore plus simple, on dirait simplissime.

   Ce qui invaliderait l’hypothèse de progression.

   Connectez-vous pour répondre
3. Sidonie

   juillet 10, 2023
   23h10

   En effet, on a trois triangles qui ont 2 cotés égaux. Si on note a l’angle le plus petit du parallélogramme deux parmi eux on a un angle a+60° entre les côtés égaux.
   Quant au 3éme un calcul simple donne 360°- 120°- (180° -a) = a +60°.
   Les 3 triangles sont égaux.

   Connectez-vous pour répondre