

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
13h04
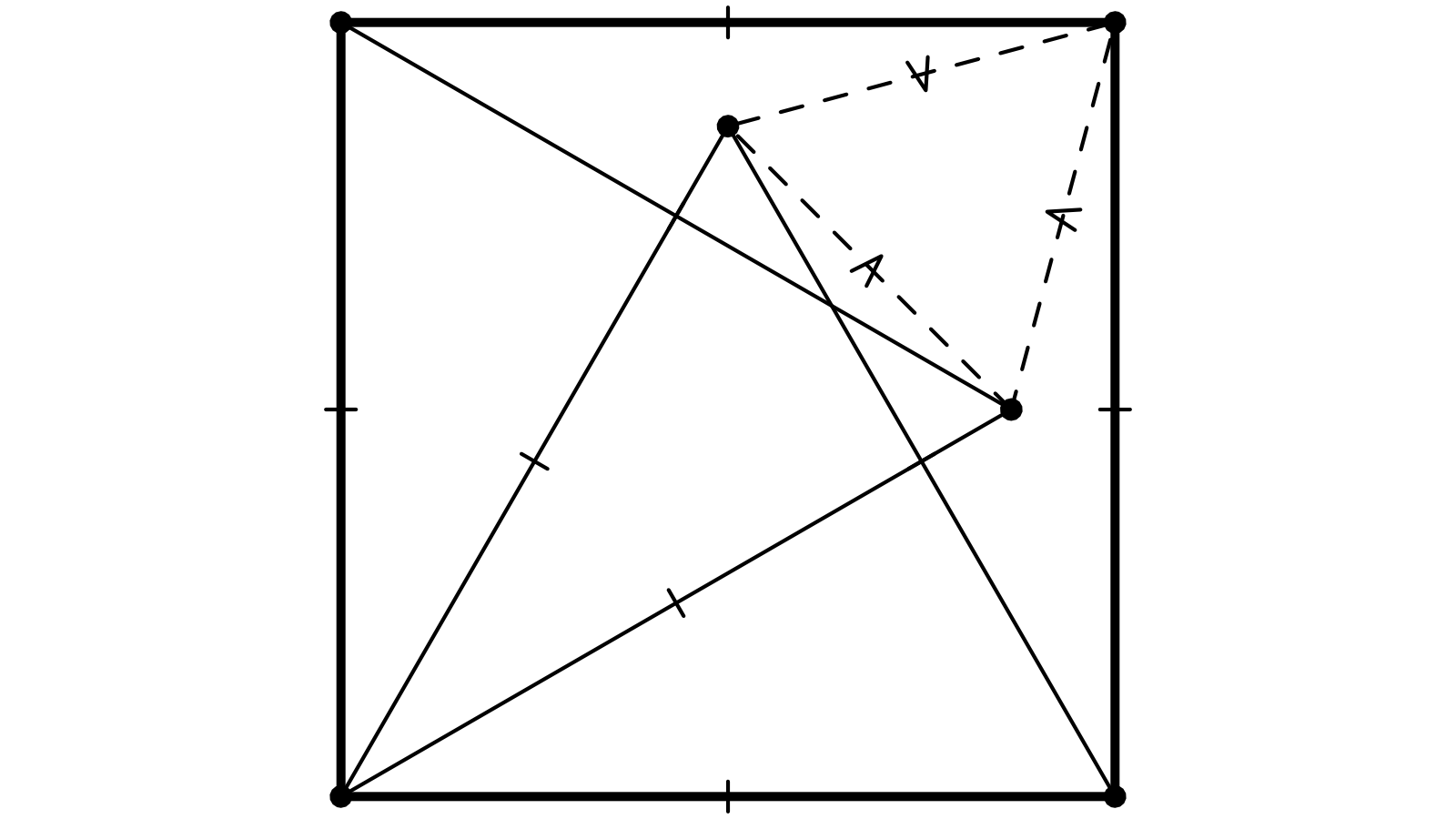
Je vois la figure, telle que proposée, comme une cousine de la précédente, elle même petite soeur de la 8.1.18. Et, telle quelle, elle comporte beaucoup trop de symétries !
Je veux dire qu’on pourrait donner une preuve de la propriété proposée (remarquant que AC est axe de symétrie, calculant tous les angles, etc), preuve qui passerait à côté de l’important. Je propose donc de remonter à l’ancêtre commun, remplaçant le carré par le parallélogramme de la figure 8.1.18.
.
Un parallélogramme, donc, ABCD, et deux triangles équilatéraux AED et ABF (En souvenir de l’ancêtre, je fais figurer ADE’ et AF’B).
Il faut alors montrer que CFE est équilatéral.
.
On voit que les triangles FCB et FEA sont égaux : côtés EA et CB, FB et FA, angles CBF et EAF égaux (si je note A, B, .. les angles sommets du parallélogramme, CBF=B-60 et EAF=120-A, deux quantités égales).
Les segments FC et FE ont donc même longueur
.
Les triangles ECD et CFB sont égaux, eux aussi (mêmes angles en B et D), d’où CE et CF de même longueur.
11h21
Vous avez raison, cette figure comporte bien trop de symétries : non seulement le carré peut être déformé en parallélogramme, mais, tout comme pour les trois Figures sans Paroles 8.1.17, 8.1.18 et 8.1.19, les triangles équilatéraux peuvent aussi être déformés en triangles quelconques. En effet, si ABCD est un parallélogramme et E et F des points tels que les triangles ADE et FBA soient directement semblables, alors FCE est toujours directement semblable à ADE et FBA.
Une preuve très simple figure sous la Figure sans Paroles 8.1.17, mais avec des notations différentes (car j’avais repris celles de Sidonie) : les points A, B, I, C, E et D de 8.1.17 correspondent à vos A, B, C, D, E et F.