

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
13h07
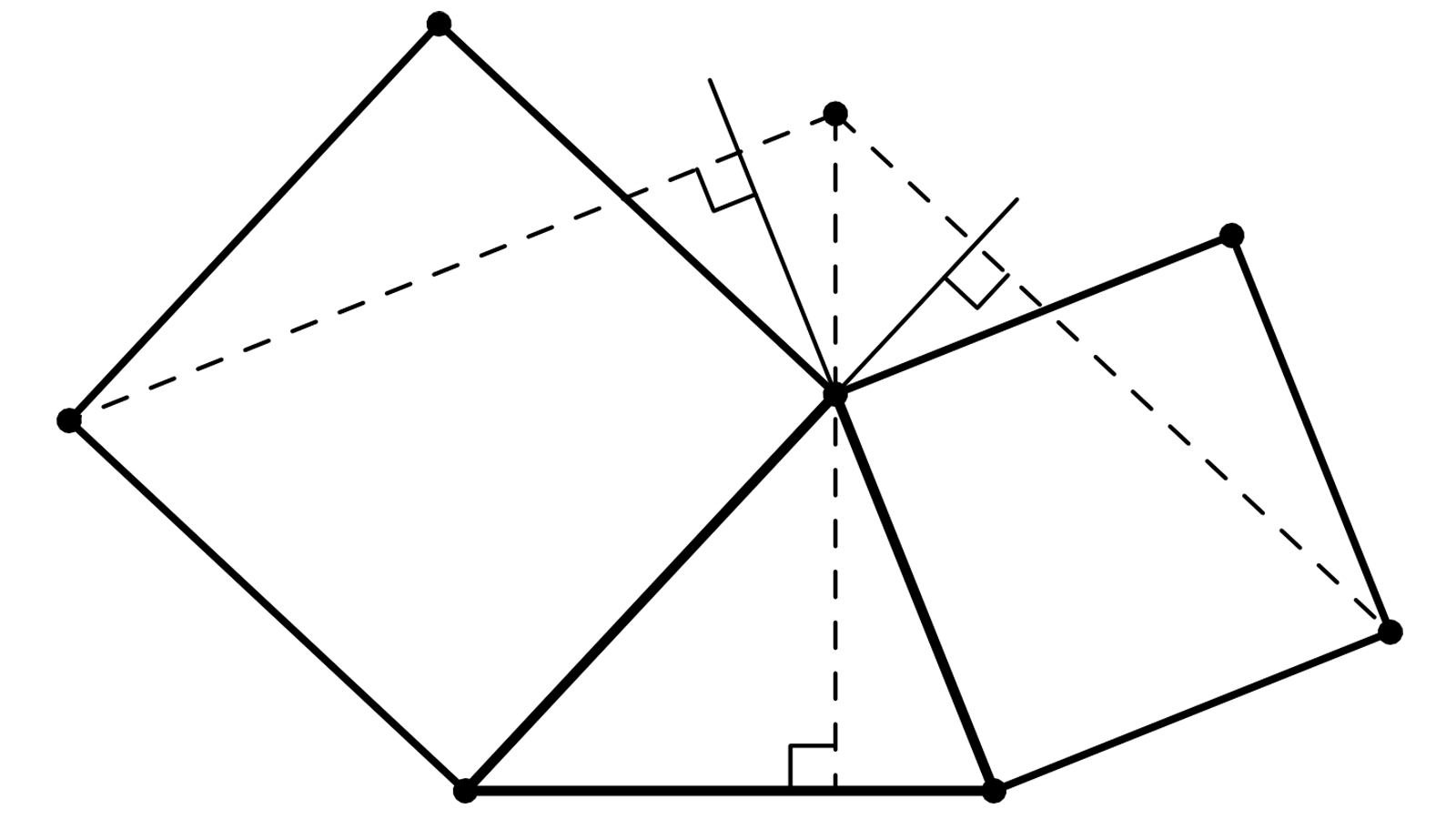
Deux carrés \(ABCD\) et \(AEFG\), construites sur les côtés \(AD\) et \(AE\) du triangle \(ADE\). \(J\) et \(K\) sont les projetés orthogonaux de \(C\) et \(F\) sur \((AE)\) et \((AD)\). \(H\) est l’intersection de \((CJ)\) et \((FK)\).
Il faut montrer l’orthogonalité de \((AH)\) et \((DE)\).
.
Je trace \((FA)\), j’appelle \(F’\) l’intersection \((FA)-(CH)\). De même \((CA)\) qui coupe \((FH)\) en \(C’\).
\(AFE\) et \(AF’J\) sont deux triangles rectangles isocèles : \((F’F,F’H)=45\)°
Même chose quant à \(ACD\) et \(AC’K\), et donc \((C’H,C’C)=45\)°.
Les triangles \(HF’F\) et \(HC’C\), dont les angles ont même valeur, sont semblables : \(HC/HC’=HF/HF’\), soit \(HF’\times HC=HC’\times HF\) (1)
(F’A,F’H)=45°=(F’A,F’C), ce qui fait que F’ appartient au cercle de centre \(D\), passant par \(A\) et \(C\). De même, \(C’\) appartient au cercle de centre \(E\) passant par \(A\) et \(F\).
La relation (1) fait alors de \(H\) un point de l’axe radical de ces deux cercles. Axe radical qui passe par A, et est perpendiculaire à DE, la ligne des centres.