

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
20h50
Bon, visiblement, ça ne marche pas.
7h31
Mais ça marche si on remplace les sommets par les centres des carrés. Je n’en ai ni la démonstration ni le temps de la faire. Avis aux amateurs.
14h13
Faute de savoir avec quelle précision vous avez construit la figure, placé les milieux, tracé les carrés, j’avoue ne pas avoir été immédiatement convaincue par le tout petit triangle entre vos trois droites pointillées. Mais vous avez bien sûr raison ; et en prenant les points D et E très voisins l’un de l’autre, l’angle entre AG et AH très petit, et le côté du carré AHIJ gigantesque, on peut considérablement agrandir ce petit triangle, jusqu’à le rendre arbitrairement proche du triangle EFG.
La règle du jeu, pour ces Figures sans Paroles, est « d’observer, de comprendre, de poser les questions suggérées, et, si possible, les résoudre ». Nous avions déjà rencontré une situation analogue avec la Figure 8.1.9 ; mais c’est seulement maintenant que je comprends que les questions que posent ces figures ne sont pas Comment montrer que … ? mais bien Est-il vrai que … ?
16h08
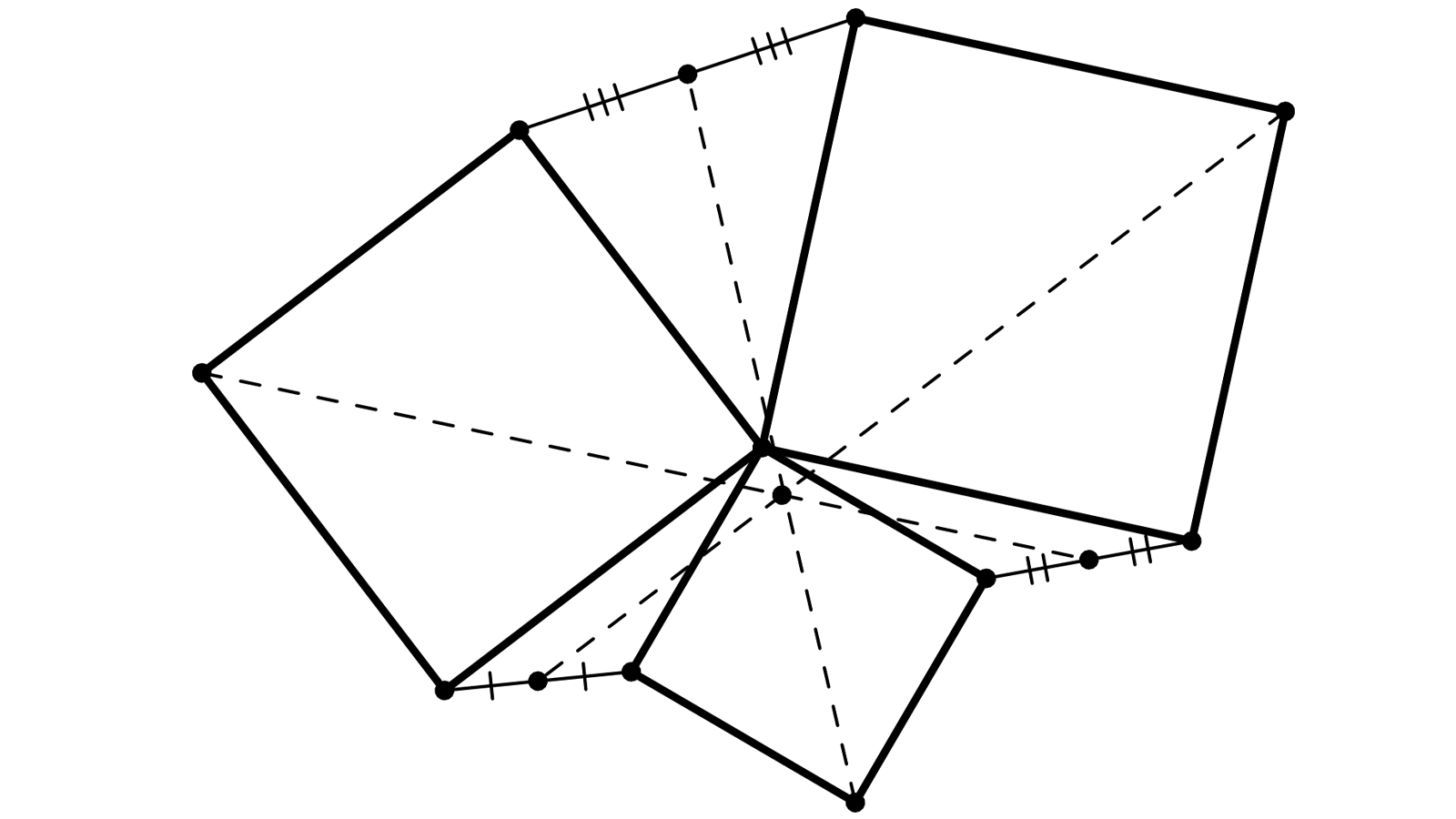
On a trois carrés, ayant un sommet A en commun : ABCD, AEFG, AHIJ.
On note K, L, M les milieux des segments BJ, DE, GH, et P, Q, R les centres des carrés (milieux de BD, GE et HJ).
Et ce sont les segments PM, QK et LR qui sont concourants.
On remarque l’analogie avec les figures passées : si on se concentre, par exemple sur les carrés ABCD et AHIJ, la figure 9.6 nous affirme que (KP,KR)=90°, que KP et KR ont même longueur.
C’est à dire que KPR est un triangle rectangle isocèle, les angles en P et R étant 45°.
Même traitement pour LQP, puis MRQ : (PL,PQ)=45°, (RQ,RM=45°, etc.
Si maintenant je trace le triangle PQR, c’est la figure 4.9.5 que je ressuscite, et on y a justifié l’intersection (PM, QK, LR)
18h49
On peut aussi remarquer que KQ, LR et MP sont les hauteurs du triangle KLM (une rotation de KQ autour du point P1 l’amène en LM, etc)