

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
12h39
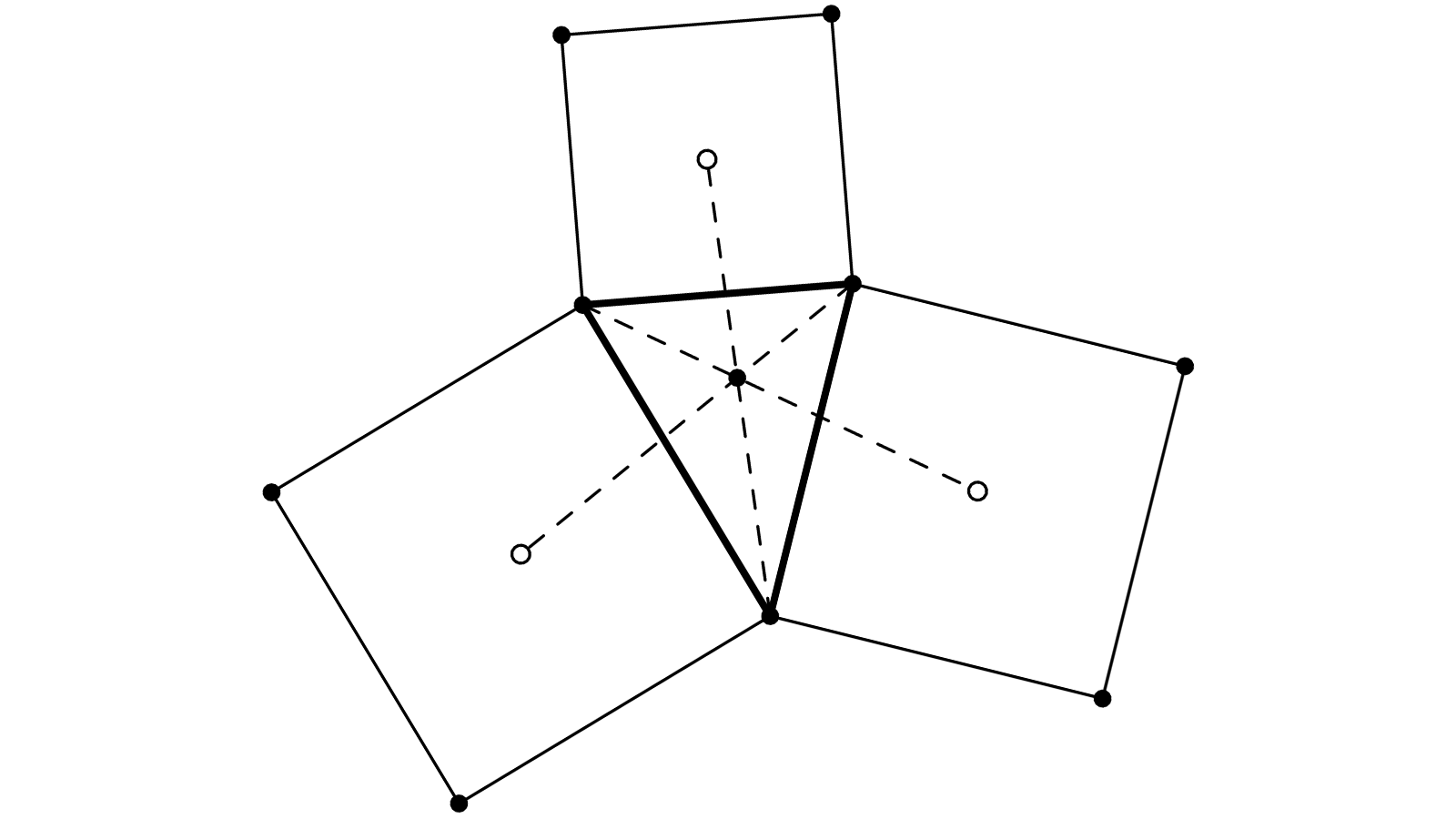
On retrouve une variante de la figure 9.1, elle-même fille de 4.9.5 ! Les centres des carrés sont liés aux sommets du triangle par des angles égaux. Dans la figure 9.1, les figures extérieures étaient des triangles équilatéraux — angles de 30°. Ici, les carrés aboutissent à la même propriété, avec des angles de 45°
20h49
Petit plus
Petit plus : les droites (IJ) et (AK) sont perpendiculaires (démonstration suit) ce qui fait de (BI), (CJ) et (AK) les 3 hauteurs, naturellement concourantes, du triangle IJK.
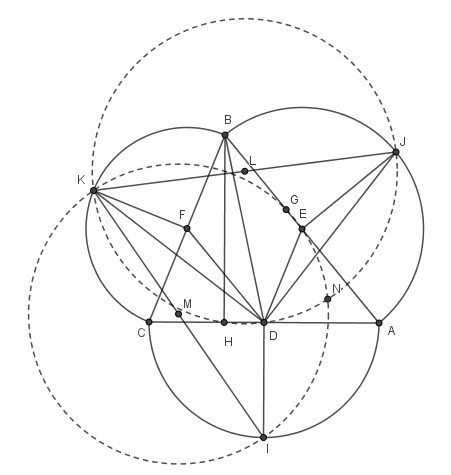
Triangle ABC. Les centres I, J et K des carrés sont ici au sommet des demi-cercles de diamètres AC, AB et BC.
D, E et F sont les milieux de AC, AB et BC. H et G sont les pieds des hauteurs issues de C et B.
L et M sont les milieux de KJ et de KI.
N est la 2éme intersection des cercles (i) et (j) de diamètres KJ et KI
Je pose b = (BC,BA) = (FC,FD) = (ED,EA) = (DE,DF)
CHBK et AHBJ sont cocycliques.
Donc (HB,HK) = (CB,CK) =π/4 et de même (HI,HB) =π/4 d’où (HI,HK)= π/2
ce qui fait que (i) passe par H et (j) passe par G
FK = FB = DE, FD = BE =EJ, (FK,FD) = a +π/2 = (ED ,EJ) donc les triangles KFD et DEI sont égaux
D’où DK = DJ (inattendu)
et (DK,DJ) = (DK,DF)+(DF,DE)+(DE,DJ) = – a + (JD,JE) + (DE,DJ) = -a +(ED,EJ) = -a +a +π/2 = π/2
Donc (j) passe par D et (i) passe par E
Or D, E, G et H sont cocycliques sur le cercle d’Euler.
La puissance de A par rapport à ce cercle donne AD.AH = AE.AG.
AD.AH est aussi la puissance de A par rapport à (i) et AE.AG est la puissance de A par rapport à (J)
A est donc sur l’axe radical de (i) et (j) d’où A, N et K alignés.
(NI) et (NJ) sont perpendiculaires à (AK) donc elles sont confondues
et pour finir (IJ) et (AK) perpendiculaires
10h22
Petit plus avec un peu moins
Séduite par votre remarque Petit plus, je vous en propose une autre démonstration, utilisant moins de points : outre les indispensables A, B, C et I, J, K, je ne garderai que D, mais introduirai un nouveau point D’.
La rotation R de sommet K et d’angle 90° envoie C sur B ; la rotation T de sommet J et d’angle 90° envoie B sur A. En effectuant R suivie de T, on a obtient la rotation S d’angle 180° envoyant C sur A, c’est-à dire la symétrie S par rapport au milieu D de CA.
Le point D’ = R(D) est envoyé par T sur S(D), c’est-à-dire sur D.
Les triangles KDD’ et JD’D étant rectangles et isocèles, KDJD’ est un carré. La rotation de centre D et d’angle 90° envoie donc J sur K. [1] Comme elle envoie aussi C sur I, elle envoie le segment CJ sur IK ; ces deux segments sont donc (égaux et) perpendiculaires.
[1] Ce n’est pas neuf, mais figure implicitement dans votre démonstration.