Dans les sciences, l’homme modélise la réalité géométrique à l’aide de la notion d’espace et de ses propriétés. Cette reconstruction formelle d’une notion si intuitive a permis des milliers d’applications : des calculs astronomiques des anciens Grecs à la programmation actuelle des mouvements des robots.
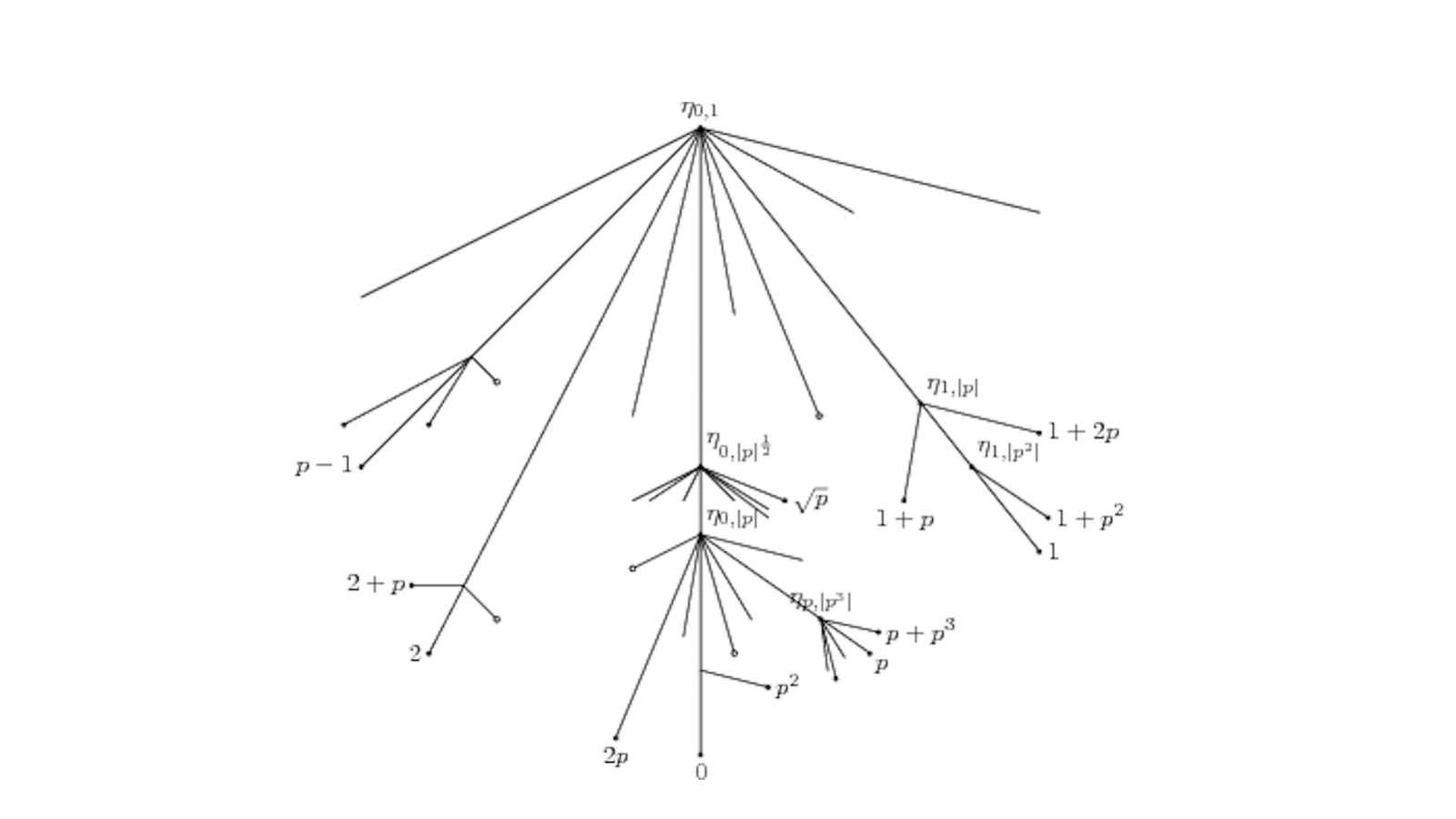
En mathématiques les différents objets géométriques conduisent à des calculs de nature différente : espaces topologiques, variétés différentiables, variétés algébriques, espaces analytiques. Un des défis récents de la recherche est de découvrir des outils pour traiter certains espaces particuliers, que l’on appelle « p-adiques ». Vers la fin des années quatre-vingt, le mathématicien russe Vladimir Berkovich a proposé une classe d’espaces qui peuvent être étudiés en profondeur de plusieurs points de vue. Ces espaces sont jolis à voir et recèlent une géométrie insolite.
ÉCRIT PAR
Daniele Turchetti
Research fellow - University of Warwick (Angleterre)
Copier l’entrée
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.