

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
11h27
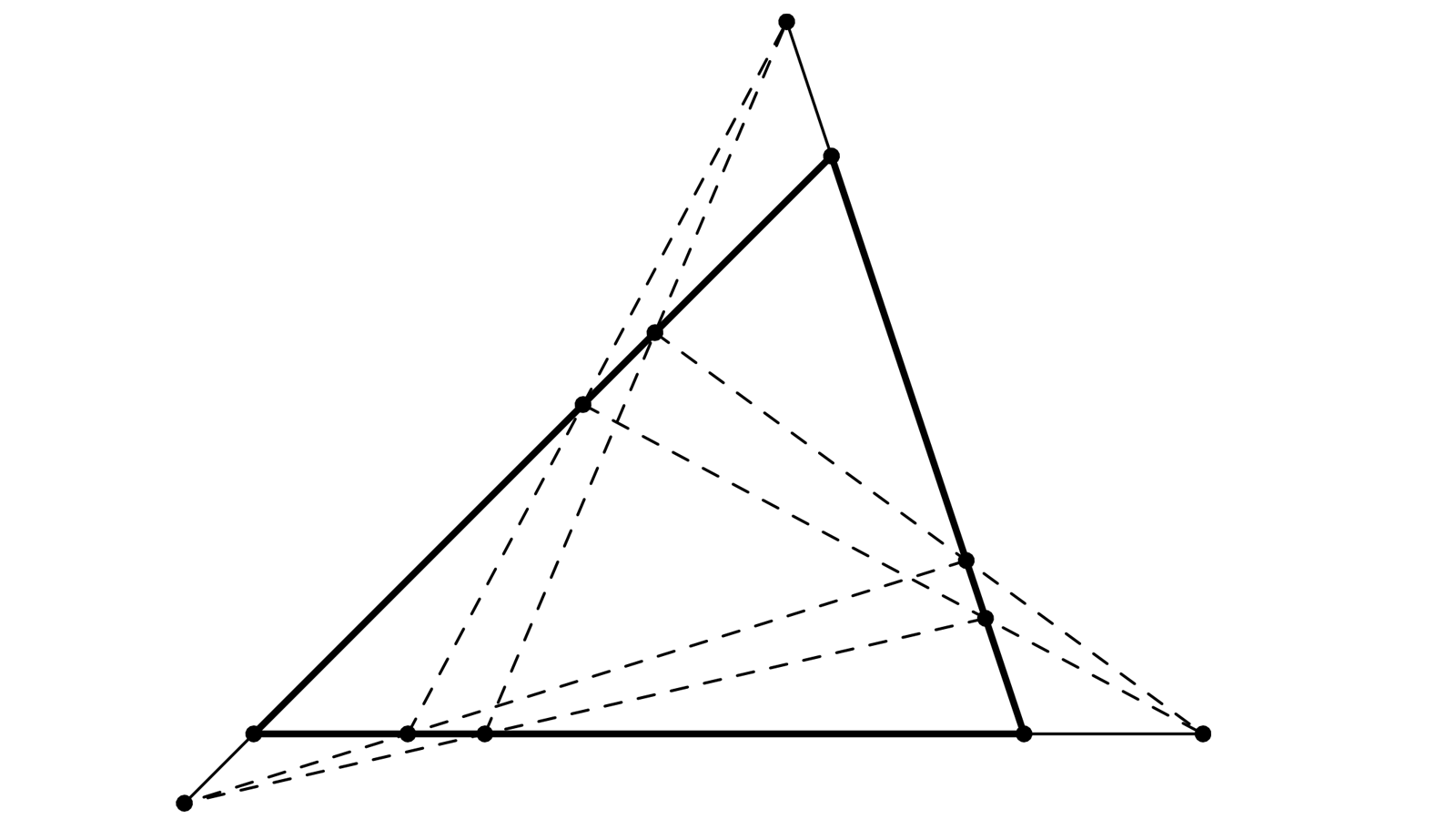
Un triangle ABC. Un point D sur AC, et deux droites issues de D, coupant AB et BC en G, E H, F.
De même, depuis N sur AB, deux sécantes coupent BC et AC en E, K et F, L.
La droite GL coupe BC en J.
Il faut alors établir l’alignement de H, K, J.
On va dérouler une autre sorte de tourniquette.
.
Le théorème de Menelaüs appliqué à \((DE)\) puis \((DF)\) dit que
\(DA\times EC\times GB= DC\times EB\times GA\) \
puis \((DF)\) : \(DA\times FC\times HB= DC\times FB\times HA\).
(il faudrait ajouter un chapeau pour bien orienter les segments)
Ce qui signifie que
\[ \frac{EC\times GB}{EB\times GA}=\frac{FC\times HB}{FB\times HA} \]
Le même traitement, su \((NK)\) et \((NL\) donne
\[ \frac{FC\times LA}{FB\times LC}=\frac{EC\times KA}{EB\times KC} \]
Le produit de ces deux égalités laisse un résultat intéressant :
\[ \frac{GB\times LA}{GA\times LC}=\frac{HB\times KA}{HA\times KC} \]
Si maintenant on s’intéresse à \((JG)\), on a \(JC\times GB\times LA =JB\times GA\times LC\), relation dans laquelle on peut injecter la relation précédente, et qui aboutit alors à
\[ \frac{JC\times HB\times KA}{JB\times HA\times KC}=1 \]
qui n’est autre que la relation de Menelaüs établissant l’alignement \(J, K, H\)
19h31
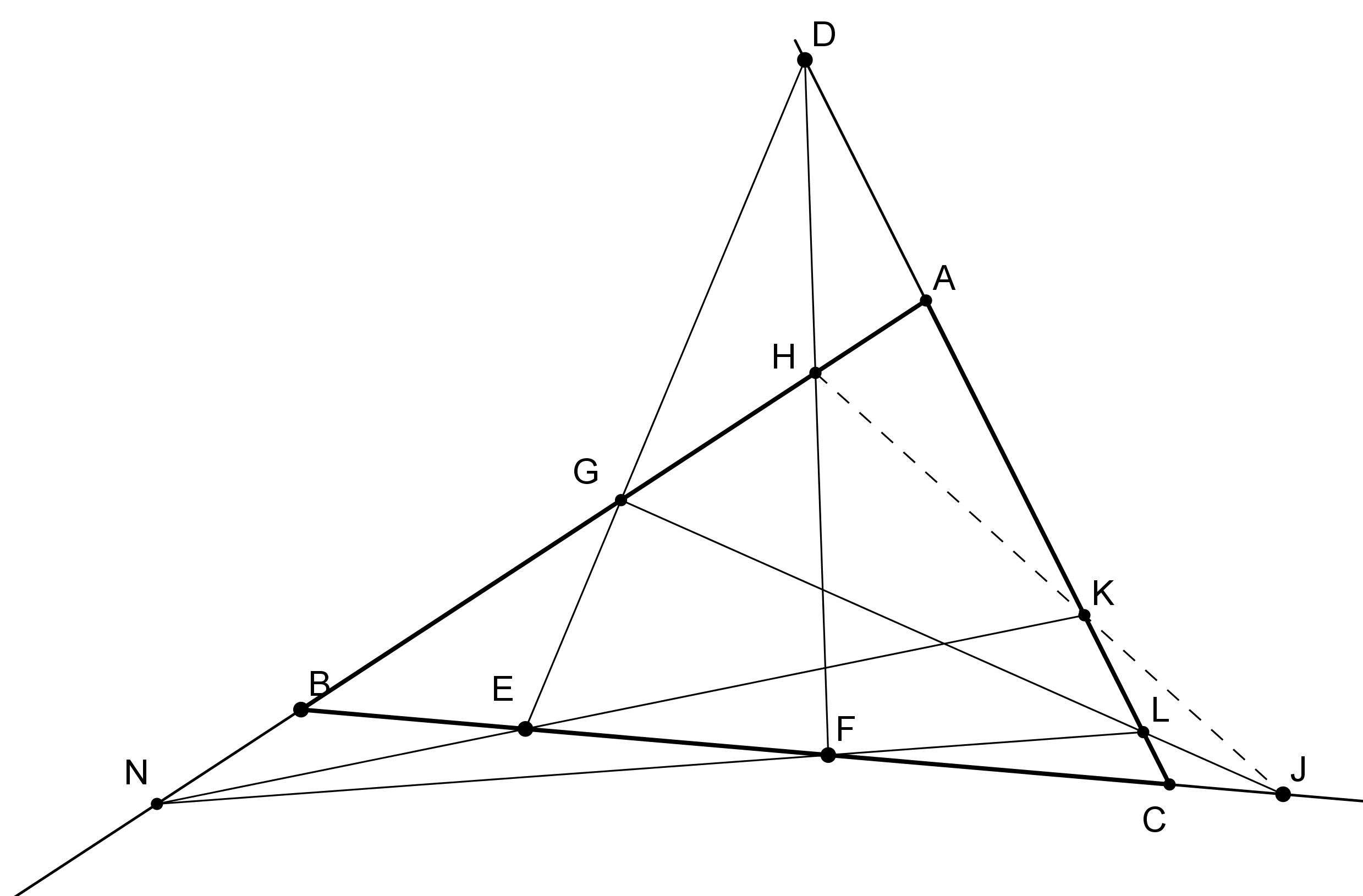
Un triangle ABC.
D est un point de la demi-droite [CA).
E et F sont deux points de [BC]. DE) et (DF) coupent [AB] en H et G.
I est un point de la demi-droite [AB).
(IE) et (IF) coupent [AC] en J et K.
Il conviendrait de montrer la concourance des droites (BC), (HK) et (GJ).
Les triangles GEK et FHJ sont tels que (GF), (EH) et (KJ) concourent en D.
D’après le théorème de Desargues L, M et N, intersections des côtés (FH) avec (GE), (FJ) avec (GK) et (HJ) avec (EK), sont alignés.
Mais alors les triangles GEK et JFH vérifient les hypothèses du théorème réciproque de Desargues.
Conclusion : (GJ), (KH) et (EF) = (AB) sont concourantes.
10h45
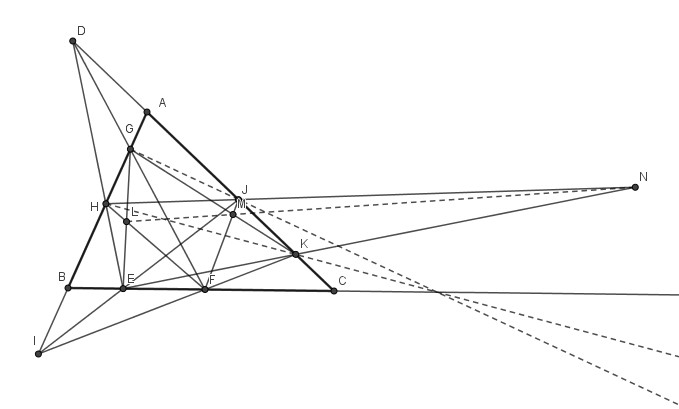
Un triangle ABC.
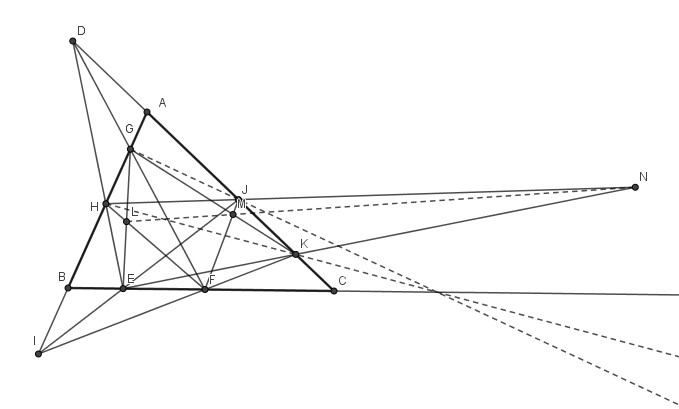
D est un point de la demi-droite [CA).
E et F sont deux points de [BC]. DE) et (DF) coupent [AB] en H et G.
I est un point de la demi-droite [AB).
(IE) et (IF) coupent [AC] en J et K.
Il conviendrait de montrer la concourance des droites (BC), (HK) et (GJ).
Les triangles GEK et FHJ sont tels que (GF), (EH) et (KJ) concourent en D.
D’après le théorème de Desargues L, M et N, intersections des côtés (FH) avec (GE), (FJ) avec (GK) et (HJ) avec (EK), sont alignés.
Mais alors les triangles GEK et JFH vérifient les hypothèses du théorème réciproque de Desargues.
Conclusion : (GJ), (KH) et (EF) = (AB) sont concourantes.