
Dimanche dernier, alors qu’en France on fêtait les amoureux, ce sont les mathématiques qui étaient célébrées à Moscou à l’occasion de la математический праздник (fête mathématique). Plutôt qu’une fête à proprement parler, c’est en réalité une sorte de compétition mathématique à laquelle participent approximativement trois cents organisateurs et un peu plus de deux mille élèves des 6ème et 7ème classes 1Ce sont, dans l’ordre, les équivalents, de la 6ème et de la 5ème en France. Lorsque je parle d’équivalent, la comparaison est faite avec l’âge des élèves, les programmes pouvant quant à eux être sensiblement différents., et parmi eux une quinzaine provenant du lycée français de Moscou. C’est afin de mieux encadrer ces derniers que les organisateurs m’ont proposé de les aider, et c’est bien sûr avec grand plaisir que j’ai accepté.
Je me suis donc retrouvé, dimanche matin, obligé de me lever de bonne heure afin de ne pas être trop en retard 2Bien sûr, j’ai tourné à un moment au mauvais endroit, ce qui m’a valu d’arriver avec une demi-heure de retard, mais n’insistons pas. au rendez-vous fixé avec un de mes collègue à 9h à l’Université d’État de Moscou où se déroule la compétition. En arrivant, j’ai été tout d’abord impressionné par l’ampleur de cette manifestation : je parlais tout à l’heure un peu abstraitement de plus de deux mille élèves, mais lorsque vous entrez dans le bâtiment en même temps qu’eux et que vous cherchez désespérément votre collègue parmi toutes ses têtes blondes (accompagnés de leurs parents ou de leurs professeurs en général), vous comprenez peut-être encore mieux ce que cela représente. En tout cas, jamais en France, je n’avais vu un tel rassemblement pour les maths (enfin, exception faite des manifestations bien entendu…).
Malgré le raffut, j’ai réussi à trouver mon camarade (n’y voyez pas de rapport avec le régime communiste), et nous sommes montés nous installer dans une petite salle dans laquelle s’est déroulée par la suite l’épreuve pour les candidats français. Bientôt, ces derniers nous ont rejoints, accompagnés de leurs professeurs, et à 10h bien sonnées l’épreuve a pu commencer. Il y a un sujet différent pour chacun de deux niveaux et chaque sujet compte six exercices, un peu dans le style olympique (voir plus bas). Une feuille d’instructions, écrite en russe, précise les règles à suivre pour le bon déroulement des épreuves. Ces règles ont l’air strictes sur le papier mais, comme souvent en Russie, elles ne sont pas respectées à la lettre et donc finalement les élèves ont composé dans une ambiance plutôt décontractée. Deux heures plus tard, un peu après midi donc, nous avons ramassé les copies et nous sommes dirigés tous ensemble vers la cantine.
L’après midi, plusieurs occupations étaient proposées aux élèves pendant que nous, nous corrigions leurs copies : une conférence, des dessins animés mathématiques, des jeux mathématiques, etc. L’aspect festif de la fête mathématique était donc quand même un peu présent. En fait, je suis mauvaise langue, il l’était bien plus qu’un peu : l’ambiance était vraiment celle d’une fête, et la bonne humeur de tous, et en particulier des enfants ou jeunes gens prenait sans équivoque le pas sur la mesquinerie et l’esprit de compétition. Bref, tout le monde s’amusait, même les correcteurs qui n’hésitaient pas à rire des copies qu’ils avaient à corriger lorsque cela le méritait. Après avoir noté les candidats français, nous sommes descendus rejoindre nos élèves et en avons profité pour résoudre quelques puzzles (illustrant le théorème de Pythagore, notamment) et se heurter à un problème de ficelle que je vous expliquerai peut-être dans un autre billet. S’en est suivi une petite correction des exercices dispensée par votre serviteur, et nous voici enfin prêts à assister à la cérémonie de clôture et à la remise des prix.
Pas de très grande originalité sur les prix puisqu’il s’agissait de diplômes et de livres ou jeux mathématiques. Un peu moins de deux cents candidats ont reçu un prix, ce qui fait donc une proportion d’environ 10%… et parmi les lauréats, pas moins de trois candidats français (ce qui, notons-le bien, fait une proportion largement supérieure). Une dernière photo de groupe… avant de nous séparer avec la larme à l’œil 3Oui, oui, j’exagère quand même un peu…. La journée n’était malgré tout pas encore tout à fait terminée puisque un repas, bien arrosé, cela va sans dire, attendait enfin les organisateurs à l’Université Indépendante.
En tout cas, j’ai passé une bonne journée. Et, pour vous faire encore mieux partager ma joie, je ne résiste pas au plaisir de recopier ci-dessous les énoncés des problèmes. Les solutions, quant à elles, sont disponibles en russe sur le site de la manifestation.
Énoncé pour les 5èmes
1. Sur un saucisson sont dessinés de fins cercles transversaux, certains rouges, certains verts et certains jaunes. Si on coupe le saucisson là où sont dessinés les cercles rouges, on obtient 5 morceaux. Si on coupe sur les cercles jaunes, on 7 morceaux. Si on coupe sur les cercles verts, on obtient 11 morceaux. Combien de morceaux obtient-on en coupant sur tous les cercles à la fois. (3 points)
2. Dans le pays de Forêtmont, il n’y a que des fées et des nains. Les nains mentent en parlant de leur or, mais dans les autres cas disent la vérité. Les fées mentent en parlant des nains, mais dans les autres cas disent la vérité. Voici les paroles de deux forêtmontains :
— J’ai volé tout mon or au Dragon
— Tu mens
Devinez par qui sont prononcées ces phrases. (4 points)
3. Le petit cochon Naf-Naf a réussi à faire un parallélépipède avec des cubes identiques, puis à le recouvrir de trois carrés de tissu de façon à ce que toute la surface du parallélépipède soit recouverte sans que jamais les carrés de tissu ne se superposent. Pouvez-vous en faire autant ? (5 points)
4. Dans un bureau de change, on exécute des opérations de deux types :
1) Contre 2 euros, on donne 3 dollars et un bonbon en cadeau
2) Contre 5 dollars, on donne 3 euros et un bonbon en cadeau
Le Schtroumpf Financier est venu au bureau de change avec seulement des dollars. Il en est reparti avec moins de dollars, sans euros et avec 50 bonbons. Combien de dollars a-t-il dépensé pour un tel « cadeau » ? (6 points)
5. En traçant des segments horizontaux et verticaux, Alexandre a divisé un échiquier \(8 x 8 \) en 30 rectangles de manière à ce que deux rectangles de même dimension (même longueur et même largeur) ne se touchent jamais (même par les angles ; voir sur le dessin). Essayez de faire mieux en divisant l’échiquier en un plus grand nombre de rectangles tout en observant la même condition. (2 points pour chaque rectangle au-dessus de 30)

.
6. Au bord d’une table ronde tournante, on a disposé 30 tasses de thé à intervalles réguliers. Le Lièvre de Mars et le Loir sont assis chacun devant une tasse de thé (pas nécessairement à côté l’une de l’autre). Après qu’il aient chacun bu leur thé, le Lièvre fait tourner la table de sorte que chacun de deux animaux se retrouve à nouveau devant une tasse pleine. Ils boivent alors leur thé, et le Lièvre refait tourner la table (peut-être d’un autre angle) de façon à placer devant les animaux une nouvelle tasse pleine. On suppose qu’il est possible de vider toutes les tasses en continuant ainsi (c’est-à-dire sans que jamais le Lièvre ni le Loir ne se retrouve en face d’une tasse vide). Montrer que, si le Lièvre avait tout simplement tourné la table de deux tasses à chaque fois (toujours dans le même sens), toutes les tasses auraient également été vidées. (8 points)
Énoncé pour les 4èmes
1. Avec sa calculatrice, Georges peut seulement multiplier un nombre par 3, ajouter 3 à un nombre, ou, si un nombre est divisible par 3, le diviser par 3. Comment sur cette calculatrice obtenir le nombre 11 en partant du nombre 1 ? (3 points)
.
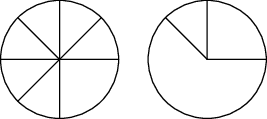
2. Sur un axe vertical on a mis plusieurs roues à rayons. La vue de dessus est représentée sur le dessin de gauche. Puis on a tourné les roues. La nouvelle vue de dessus est représentée sur le dessin de droite. Est-il possible qu’il y ait sur cet axe : a) trois roues ; b) deux roues ? (Si oui, dessiner les roues) (2 points + 3 points)
3. Des enfants ont mangé des bonbons. Chaque enfant a mangé sept bonbons de moins que tous les autres enfants réunis. Chaque enfant a mangé au moins deux bonbons. Combien de bonbons ont été mangés au total ? (5 points)
4. Le Coq, la Corneille et le Coucou participent à un concours de chant. Chaque membre du jury a voté pour un des trois candidats. Le Pivert a compté qu’il y avait 59 juges dans le jury. Il a compté que 15 juges ont voté soit pour le Coq soit pour la Corneille, que 18 juges ont voté soit pour la Corneille soit pour le Coucou, et que 20 juges ont voté soit pour le Coucou soit pour le Coq. Dans ses calculs le Pivert s’est trompé, mais la différence avec les nombres corrects ne dépasse jamais 13. Combien de juges ont voté pour la Corneille ? (6 points)
5. a) Le petit cochon Naf-Naf a réussi à faire un parallélépipède avec des cubes identiques, puis à le recouvrir de trois carrés de tissu de façon à ce que toute la surface du parallélépipède soit recouverte sans que jamais les carrés de tissu ne se superposent. Pouvez-vous en faire autant ? (3 points)
b) Est-ce que Naf-Naf peut faire en sorte qu’en plus chaque carré de tissu touche les deux autres ? (4 points)
6. Un assortiment de navires pour la bataille navale se compose d’un porte-avions (4 cases), deux croiseurs (3 cases), trois torpilleurs (2 cases) et quatre mines flottantes (1 case). Il est facile de placer un tel assortiment sur une grille \(10×10\) sans que deux navires ne se touchent, même par les angles. Quelle est la taille minimale d’une grille carrée sur laquelle on peut placer un tel groupe de navires avec la même contrainte ? (8 points)


9h37
Pour un équivalent français, je vous conseille de vous rendre à la finale du Concours internationale de Jeux Mathématique et Logique, organisé tous les été dans la cité étudiante de Paris http://ffjm.cijm.org/
Il y a des élèves du primaire jusqu’au lycée et le mot international n’est pas usurpé, ce qui rend ce concours très impressionnant, et visiblement pris très au sérieux par presque tous les pays participant (sauf justement les Parisien qui, comme moi, n’ayant que le RER à prendre pour venir, et non pas l’avion comme le groupe de québecois que j’y vis, se rendent moins compte de l’importance du concours).
20h09
Oui, je connais la FFJM et, bien que ne m’étant jamais rendu à une de leurs finales, je ne doute pas que cela puisse être une manifestation de grande ampleur.
Sans remettre en cause ce que vous dites, j’ai malgré tout l’impression, en lisant votre description, que ce dont vous parlez est un peu différent de la fête mathématique que je décrivais. En effet, alors que la finale internationale de la FFJM est, comme son nom l’indique sans équivoque, une finale internationale, la fête de mathématique à Moscou est au contraire une entrée dans ce type de compétitions. Pour la plupart des élèves qui ont composés dimanche dernier, il s’agissait de leur première « olympiade » [1] et je ne crois pas non plus que beaucoup aient fait un long voyage pour venir composer (en tout cas, ça s’appelle bien la fête mathématique de Moscou).
[1] Il était bien stipulé (en russe, j’espère donc que je ne fais pas un contre-sens) sur la feuille d’instructions que la plupart des élèves n’étaient pas du tout familiers avec le déroulement de ce genre d’épreuves et qu’il était donc important de bien leur lire toutes les instructions. Bien sûr, ça ne veut pas forcément dire grand chose, mais j’ai quand même l’impression que ça sous-entend (1) que ce n’est pas une épreuve à laquelle on accède après avoir passé moultes qualifications et (2) qu’il n’est pas du tout absurde de penser que les examinateurs/surveillants croient que ce type de règles fait partie de la culture du collégien moyen.