
Quand le métier de chercheur est-il apparu ? Est-ce lors de la création du CNRS, le 19 octobre 1939 ? Cette institution a été préfigurée par d’autres, et en particulier la Caisse nationale des sciences (devenue Caisse nationale de la recherche scientifique en 1935), née le 16 avril 1930 sous l’impulsion de Jean Perrin et André Mayer, soutenus par Marie Curie.
La Caisse nationale des sciences versait des bourses (et non des salaires accompagnés de charges sociales), à taux plein ou en cumul d’une autre activité professionnelle. On peut considérer qu’elle a recruté les premiers chercheurs de métier en France. La majorité des bénéficiaires étaient jeunes, avec une fraction importante de femmes. La première mathématicienne recrutée par la Caisse nationale des sciences fut Marie Charpentier, qui, de l’automne 1932 à décembre 1934, a bénéficié d’une bourse à taux partiel, en cumulant avec un emploi de maîtresse d’internat, à La Roche-sur-Yon puis à Tours.

Congrès international des mathématiciens 1932 à Zurich
Née en 1903, Marie Charpentier soutient sa thèse à Poitiers en 1931, puis elle bénéficie d’une bourse de la fondation Rockefeller pour un séjour d’un an à Harvard, en 1931-1932, à l’invitation de George Birkhoff. Elle participe au Congrès international des mathématiciens à Zurich en 1932, où elle donne une conférence invitée. La photo ci-contre a été prise lors de ce congrès. Les postes à l’université étant à l’époque pratiquement inaccessibles aux femmes – en mathématiques en tout cas – Marie Charpentier choisit de passer l’agrégation féminine (elle demande la suspension de sa bourse et vit d’une maîtrise d’internat à Angoulême), en 1935 et jusqu’à son succès en 1936. À la rentrée 1936, elle est nommée professeure au lycée de jeunes filles de Nancy. Elle obtient un congé et peut se consacrer à la recherche, à Paris, grâce à une bourse de la Caisse nationale de la recherche scientifique à taux plein en 1937-1938 et en 1938-1939. Cette bourse n’étant pas renouvelée, elle rejoint l’enseignement secondaire, qui l’affecte dans des lycées de jeunes filles à Besançon, puis à Bordeaux. Le 12 novembre 1942, elle est chargée de la maîtrise de conférences de mathématiques de la faculté des sciences de Rennes (le titulaire de la maîtrise était Claude Chevalley, parti avant-guerre en mission aux États-Unis), puis elle est promue au rang de professeure en 1947. Cette année-là, elle passe quelques mois à l’Institute for Advanced Study à Princeton, un des hauts lieux de la science à l’époque. On voit combien la carrière de Marie Charpentier a été difficile, et on soupçonne le rôle que la Caisse nationale des sciences a pu jouer pour permettre aux femmes de se faire une place dans le monde universitaire : le nouveau métier de chercheur a aidé à faire évoluer les métiers universitaires traditionnels.

Marie Charpentier
Comme la majorité des chercheuses de la Caisse nationale des sciences dans les années 30, Marie Charpentier était célibataire et elle l’est restée. On lui disait « Mademoiselle ». Jean-Pierre Escofier, un de ses collègues recruté comme assistant à l’Université de Rennes en 1964, écrit à son sujet : « Je me souviens de ses parties de tennis avec ses assistants qui étaient priés de lui envoyer la balle là où elle pouvait la renvoyer ; elle était aussi très engagée dans l’aide aux détenus des prisons de Rennes. » Elle n’est sans doute pas étrangère au fait que deux autres mathématiciennes soient devenues professeures à Rennes, en 1954 et en 1958. Elle a pris sa retraite en 1973 et est décédée en 1994.
Marie Charpentier a publié abondamment de 1930 à 1939, puis à nouveau en 1946. J’ai dénombré 20 articles dans des revues de mathématiques, dont 9 notes aux Comptes rendus de l’Académie des sciences de Paris. La thèse de Marie Charpentier, intitulée Sur les points de Peano d’une équation différentielle du premier ordre, porte sur la question de la détermination de la solution d’une équation différentielle par sa condition initiale.


Qu’est-ce qu’une équation différentielle ?
Un exemple d’équation différentielle, c’est \(y’=-\tau y\), qui gouverne la décroissance de la masse d’un matériau radioactif: dans l’espace d’une année (durée qu’on peut considérer comme infiniment petite en comparaison de la demi-vie de l’atome d’uranium 238U, par exemple), une fraction constante \(\tau\) de la masse \(y\) est transformée en un autre élément (pour l’238U, cette fraction vaut \(\tau=1{,}551\cdot10^{-10}\)). Si le phénomène de décroissance est influencé par des grandeurs qui varient dans le temps, \(\tau\) devient lui-même une fonction du temps, l’équation prend la forme \(y’=\tau(t)y\). La quantité de masse qui disparaît n’est pas toujours proportionnelle à la masse disponible, la dépendance est donnée par une fonction \(f\), \(y’=f(y)\) si le phénomène est indépendant du temps, \(y’=f(t,y)\) sous la forme la plus générale. Les solutions de l’équation différentielle sont des fonctions du temps, \(t\mapsto y(t)\). Par exemple, pour la décroissance radioactive, la solution qui au temps \(t_0\) vaut \(y_0\) est donnée par la formule \(y(t)=y_0\exp\bigl(-\tau(t-t_0)\bigr)\).
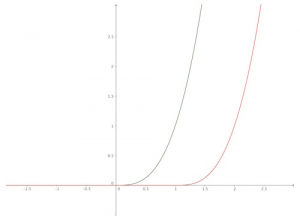
Deux solutions d’une équation différentielle du premier ordre
Depuis Cauchy, on sait que si la fonction \(f\) est dérivable par rapport à \(y\), la condition initiale \(y_0\) détermine uniquement la solution. Ce n’est plus vrai pour une dépendance moins régulière. Par exemple, lorsque \(f(y)=3|y|^{2/3}\), avec comme condition initiale \(y_0=0\) en \(t_0=0\), la fonction nulle et la fonction qui est nulle pour \(t<0\) et qui vaut \(t^3\) pour \(t>0\) sont toutes deux solutions de l’équation différentielle. On peut construire encore davantage de solutions: pour chaque \(t_1>0\), la fonction nulle pour \(t < t_1\) et qui vaut \((t-t_1)^3\) pour \(t>t_1\) en est une. Les {points de Peano} de l’équation différentielle (du nom du mathématicien italien [?Giuseppe Peano] qui le premier a étudié ce phénomène), sont les points \((t_0,y_0)\) du plan où passent une infinité de solutions. Sont-ils fréquents? Marie Charpentier montre que sur chaque droite verticale, ils sont en nombre au plus dénombrable. Son argument consiste à démontrer que l’application qui à un point \(p\) d’une droite verticale associe le faisceau \(H(p)\) des solutions qui passent par ce point possède des limites à droite et à gauche de chaque point. Autrement dit, elle raisonne sur une fonction à valeurs dans un ensemble d’ensembles, point de vue abstrait qui est encore peu répandu en 1930 (elle en attribue la paternité à Jacques Hadamard et à ses continuateurs Maurice Fréchet et Paul Montel).
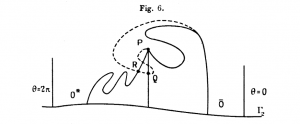
Une « courbe fermée remarquable » de Birkhoff
Ce travail qui mêle topologie et équations différentielles a dû attirer l’attention du mathématicien américain George D. Birkhoff, l’un des fondateurs de la théorie des systèmes dynamiques. Un système dynamique, c’est un système qui évolue au cours du temps, souvent selon une loi qui, elle, ne varie pas dans le temps (comme le principe fondamental de la dynamique, par exemple). La loi peut exprimer la variation infinitésimale de l’état, et donc conduire à une équation différentielle. On peut aussi se contenter d’examiner le système à intervalles réguliers, toutes les heures par exemple. En l’espace d’une heure, le système passe d’un état \(p\) à un autre état \(T(p)\), la loi est vue comme une transformation \(T\) d’un espace d’états. Birkhoff a étudié un modèle simple, où l’espace d’états est le plan. Il suppose le plan divisé en deux régions invariantes, séparées par une frontière commune \(F\). Il construit un exemple où \(T\) a grossièrement l’allure d’une rotation sur chacune des régions, mais avec des angles différents. Il montre que l’ensemble \(F\), bien que d’un seul tenant, ne peut pas être une courbe. Qu’est-ce, alors? Marie Charpentier, lors de son stage postdoctoral à Harvard, mfn]C’est un anachronisme! [/mfn] démontre que \(F\) ne peut pas être décomposé en deux sous-ensembles fermés et d’un seul tenant. C’est la première fois qu’un objet topologique aussi étrange apparaît naturellement. Bien plus tard, on comprendra que les continus indécomposables sont omniprésents en systèmes dynamiques: ils font partie du zoo des attracteurs étranges.
C’est ce résultat que Marie Charpentier présente au congrès international des mathématiciens, à Zürich, en 1932. Depuis, il a été rédémontré puis amélioré et complété par de nombreux auteurs (on trouve des références de façon continue jusqu’en 2018 inclus), car les exemples de Birkhoff jouent un rôle central en systèmes dynamiques.
Références :
- Birkhoff, George D. Sur quelques courbes fermées remarquables. Bull. Soc. Math. France 60 (1932), 1-26.
- Escofier, Jean-Pierre (2016), Petite histoire des mathématiques, Dunod, p. 194, ISBN 9782100747702.
- Yvette Kosmann-Schwarzbach : Women mathematicians in France in the mid-twentieth century, Journal of the British Society for the History of Mathematics, vol. 30, n° 3 (2015), 227-242. Lire la prépublication.
- Le Calvez, Patrice : Propriétés des attracteurs de Birkhoff. Ergodic Theory Dynam. Systems 8 (1988), no. 2, 241–310.
- Leloup, Juliette (2009), L’entre-deux-guerres mathématique à travers les thèses soutenues en France, Thèse de l’université Pierre et Marie Curie. Lire la thèse en ligne.
- Sonnet, Martine : Genre et partage du travail scientifique aux origines du CNRS (France, années 1930), Documents de travail du MAGE, 2006, n° 9, p. 225-235. Lire l’article.
- Sonnet, Martine : Les chercheuses de la Caisse nationale des sciences en France dans les années 1930 : l’insertion immédiate des femmes dans un métier neuf. In Femmes, savoir, sciences et universités, actes du colloque de Varsovie, 21-23 octobre 2016, éditions Garnier, à paraître à l’automne 2019.
Bibliographie de Marie Charpentier
- Charpentier, Marie : Sur les points de Peano d’une équation différentielle du premier ordre. C. R. Acad. Sci. Paris 191, 509-511 (1930).
- Charpentier, Marie : Sur l’existence des points de Peano d’une équation différentielle du premier ordre. C. R. Acad. Sci. Paris 191, 912-914 (1930).
- Charpentier, Marie : Sur l’intégrale supérieure d’une équation y′=f(x,y). Bulletin Sc. math. (2) 54, 203-209 (1930).
- Charpentier, Marie : Sur l’extension du problème de Baire à certaines dépendances considérées dans la théorie des équations différentielles. Bulletin Acad. Bruxelles (5) 17, 578-582 (1931).
- Charpentier, Marie : Sur une certaine classe de points de Peano. C. R. Acad. Sci. Paris 192, 139-141 (1931).
- Charpentier, Marie : Sur les points de Peano des équations y′=f pour lesquelles l’unicité de la solution est assurée d’un côté. C. R. Acad. Sci. Paris 192, 401-403 (1931).
- Charpentier, Marie : Sur un problème de topologie posé par la théorie des équations différentielles y′=f(x,y). Bull. Int. Acad. Polon. Sci. A 1931, No. 3, 191-195 (1931).
- Charpentier, Marie : Sur les lois de dependance de l’intégrale de l’équation différentielle y′=f(x,y) vis à vis de son point d’origine. Mathematica, Cluj 5, 65-99 (1931).
- Charpentier, Marie : Sur les ensembles semi-fermés et leurs applications dans la théorie des points de Peano. C. R. Acad. Sci., Paris 192, 913-915 (1931).
- Charpentier, Marie : Sur des courbes fermées analogues aux courbes de M. Birkhoff. Verhandlungen Kongreß Zürich 1932, 2, 202-203 (1932).
- Charpentier, Marie : On certain dynamical systems with points of Peano. Bull. Am. Math. Soc. 38, 849-854 (1932).
- Charpentier, Marie : Sur les intégrales d’un système de deux équations différentielles du premier ordre. Bull. Sci. Math., II. Ser. 56, 212-218 (1932).
- Charpentier, Marie : Sur des courbes fermées et leurs bouts premiers. C. R. Acad. Sci., Paris 196, 1195-1197 (1933).
- Charpentier, Marie : Sur la semi-continuité d’inclusion des trajectoires de la dynamique. C. R. Acad. Sci., Paris 196, 1771-1773 (1933).
- Charpentier, Marie : Sur quelques propriétés des courbes de M. Birkhoff. C. R. Acad. Sci., Paris 198, 701-703 (1934).
- Charpentier, Marie : Sur quelques propriétés des courbes de M. Birkhoff. Bull. Soc. Math. Fr. 62, 193-224 (1934).
- Charpentier, Marie : Sur des courbes fermées analogues aux courbes de M. Birkhoff. J. Math. Pures Appl., IX. Sér. 14, 1-48 (1935).
- Charpentier, Marie : Sur les points de Peano de certains systèmes d’équations différentielles. C. R. Acad. Sci., Paris 206, 1347-1349 (1938).
- Charpentier, Marie : Sur certaines courbes fermées et leurs bouts premiers. Bull. Sci. math. (2) 63, 303-307 (1939).
- Charpentier, Marie : Sur un faisceau de courbes intégrales de section non localement connexe. Bull. Sci. Math., II. Ser. 70, 151-155 (1946).
Post-scriptum
Pierre Pansu remercie Isabelle Dujonc, Sylvain Duquesne, Jean-Pierre Escofier, Denis Guthleben, Yvette Kosmann-Schwarzbach, Martine Sonnet.
Retrouvez tous les billets publiés à l’occasion des 80 ans du CNRS.

