Activité Streetmath de Mathématiques Vagabondes. Chapitre 2.

Notre association Mathématiques Vagabondes fait vivre l’art et la science à travers des expériences partagées, avec une attention particulière portée aux mathématiques. Notre projet Streetmath, lancé en mai 2020, fait exister des images des mathématiques dans l’espace public. Le projet consiste en une série de rencontres régulières pour créer des œuvres collectives éphémères à la craie (principalement à Lyon).

Ce billet fait suite à celui-là décrivant nos cinq premières activités Streetmath (triangle de Sierpinski; tresses, nœuds et entrelacs; mandalas; courbe rien qu’avec des droites et, enfin, pavage de Vasarely). Nous proposons ici des fiches qui retracent nos trois nouvelles activités, consacrées aux pavages de Truchet, aux courbes et leurs indices, ainsi qu’aux broderies hitomezashi. Nous espérons qu’elles vous seront utiles pour faire du Streetmath sur une place centrale (ou pas) de votre ville, sur les murs de votre village, dans une cour de votre école… Tout simplement là où vous vivez ou par où vous passez !

À savoir avant de se lancer

Matériel. Vous aurez besoin de grosses craies de trottoir (compter 5-7 craies par personne et par heure), d’un peu d’eau et d’éponges pour effacer – en cas d’erreur.

Avec qui. Tou·tes les volontaires ! Nous avons l’habitude de lancer l’appel sur nos réseaux, cela nous aide à constituer un groupe de volontaires avec un public très varié, au moins en âge (de 3 à 9 ans). Puis, d’autres personnes vont nous rejoindre une fois sur place… des passants, ce qui nous emmène de chouettes rencontres et discussions. Certain·es vont nous rejoindre pour un petit moment ou jusqu’au bout, les autres empruntent les craies pour dessiner leurs œuvres libres à côté — nous aimons beaucoup tout cela. Les tout petits sont irrésistiblement attirés par les craies mais pas toujours d’accord pour suivre des instructions précises, ce qui rajoute du charme à cette création spontanée. L’activité reste très adaptée aux familles, avec des enfants à partir de 6 ans.

Dessin du triangle de Sierpinski, et on colorie comme on veut ! Lors d'une activité à la bibliothèque de Gerland sur ce sujet, les enfants ont commencé à colorier des cases avec les drapeaux de différents pays (en commençant par le leur). C'était magnifique et nous a permis de nous rendre compte de la variété des histoires des personnes qui étaient en train de partager les mathématiques ensemble.

Où et quand. Assurez-vous que le lieu correspond à l’activité proposée (pas trop de passage, place suffisante, dallage adapté au motif, qualité du sol – un sol granuleux demande beaucoup de craie !), et que le temps est bon (éviter Streetmath sur le sol mouillé !).

Pavage de Truchet

Pavage de Truchet linaire, fait par 20 personnes (dont 10 enfants) en 2h. Si vous regardez attentivement, vous pourrez y trouver une erreur ! (nous aimons bien et assumons pleinement nos erreurs pavagesques :)))

Lieu. Place quadrillée (dalles carrées ou dalles rectangulaires subdivisées en avance).

Principe mathématique. Un pavage de Truchet est un pavage du plan par les tuiles carrées comme ici :

Ces tuiles peuvent être placées de manière régulière (avec des symétries axiales ou de translation) ou aléatoire, en suivant ou non la règle de concordance des bords (noir contre noir, blanc contre blanc). Dans ce dernier cas, le pavage est dit linéaire. On peut imaginer de nombreuses variations autour du motif  « diagonale du carré », comme par exemple sur la figure ci-dessus.

Mise en place. En cas de pavés trop grands (grands carrés ou rectangles de dimension 2:1), subdiviser les pavés pour obtenir un quadrillage en tuiles carrées de côté <20cm (ça peut être plus grand en cas de motif peu colorié).

Déroulement. En cas de pavage aléatoire, colorier chaque dalle de manière aléatoire. Cela permet de réfléchir ensemble sur comment on définirait l’aléatoire : en lançant un dé (on peut acheter des dés rebondissants en plastique), en prenant mod n le nombre de fenêtres sur un bâtiment choisi sur la place, en prenant mod n un chiffre dans l’expression décimale de nombre π, en prenant une somme du nombre de doigts choisis par 2 personnes de manière indépendante, et puis questionner chacune de ces propositions…

En cas de pavage linéaire, colorier une première tuile, qui sera un coin du pavage, puis continuer le pavage ligne par ligne et colonne par colonne.

Pour éviter les erreurs de concordance, on pourra marquer les dalles avant de les colorier, et charger une ou deux personnes de vérifier continuellement le motif global.

Conseils Il est visuellement intéressant que toute composante connexe (région fermée) soit unicolore. Pour ce faire, on peut, au choix : 

• attendre que les régions se referment avant de les colorier (une seule région ouverte en cours de coloriage)
• tout colorier d’une seule couleur (attention à la pénurie de craie !)
• mélanger les couleurs aux frontières pour obtenir des dégradés, ce qui permet de ne pas attendre (attention aux éclats de verre par terre !)

Indice de la courbe

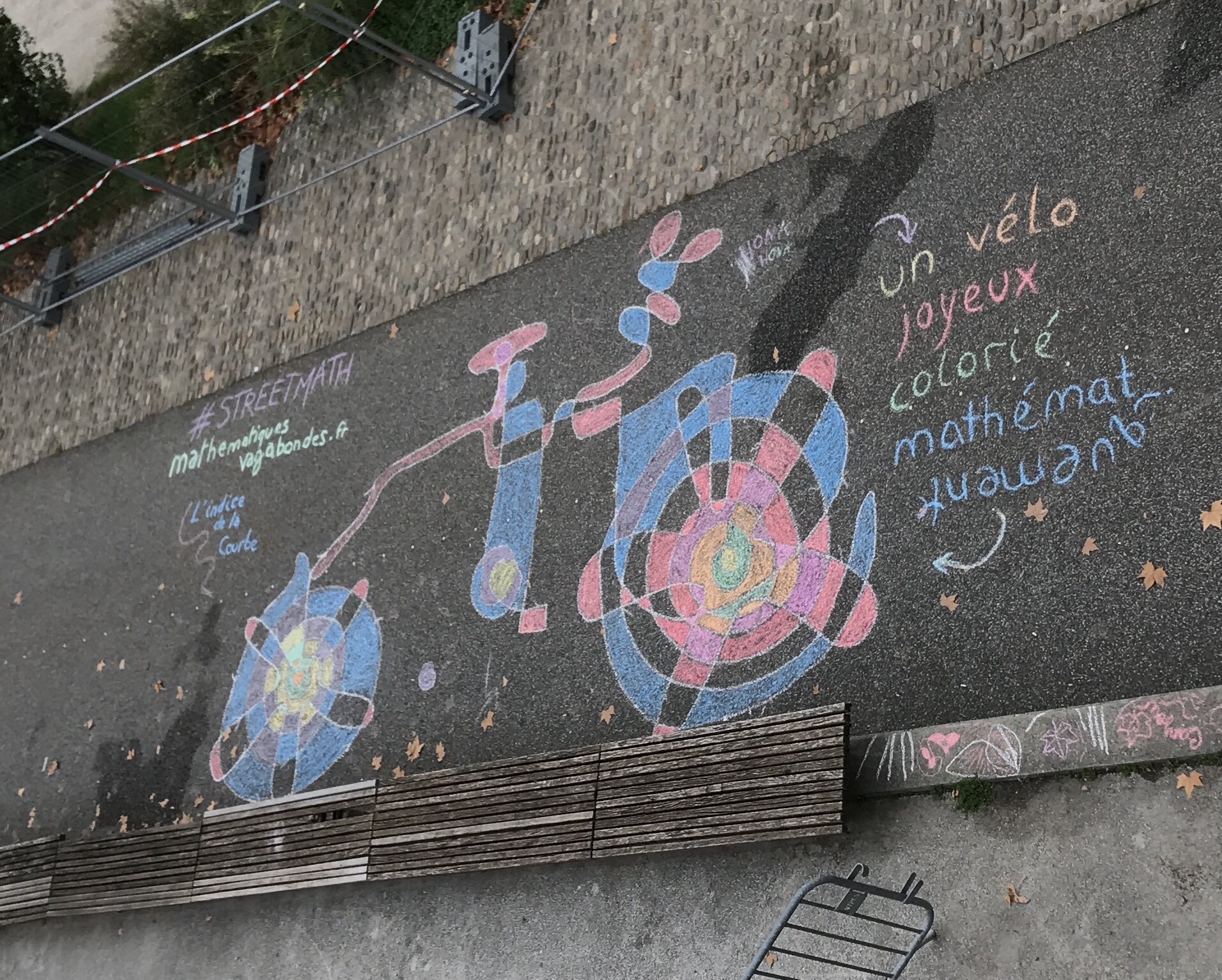
Un vélo fait par 8 personnes en 1h

Lieu. Un espace vierge.

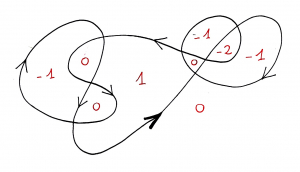
Principe mathématique. Une courbe fermée orientée avec un nombre quelconque de croisements simples définit un certain nombre de régions, qui présentent la caractéristique suivante : à l’intérieur de la région, l’indice de n’importe quel point par rapport à la courbe (c’est-à-dire le nombre de tours que fait la courbe autour du point ; voir l’article Wikipédia pour plus de détails) est le même. L’indice d’un point par rapport à la courbe est formellement défini par une intégrale, mais il existe un moyen pratique très simple de le calculer région par région, de proche en proche.

En associant une couleur à chaque entier, on colorie la région selon l’indice de ses points par rapport à la courbe.

Mise en place. Tracez une courbe fermée et orientez-la en dessinant des flèches régulièrement le long de la courbe. Associez une couleur aux premiers entiers positifs et négatifs.

Déroulement. Commencez par noter l’indice dans chaque région, selon les règles suivantes : à l’extérieur, l’indice est nul, et il augmente ou diminue à chaque fois qu’on traverse la courbe, selon que la courbe aille vers la droite ou vers la gauche.

Émerveillez-vous du fait que le nombre obtenu ne dépend pas du chemin emprunté ! Quand toutes les régions sont numérotées, vérifiez que deux régions voisines diffèrent toujours de 1 (si ce n’est pas le cas, revérifiez tout jusqu’à trouver l’erreur).

Puis coloriez, en associant à chaque nombre sa couleur.

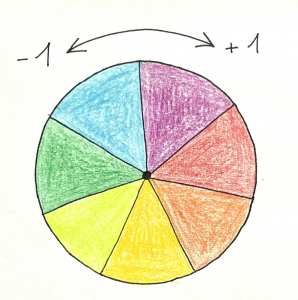
Conseils. Pour les plus jeunes, on peut commencer par de petits motifs. Si on n’a que 7 couleurs, on peut dire que 0=7, -1=6, -2=5, etc. Pour ceux qui ne seront pas familiers avec l’arithmétique modulaire, une roue des couleurs aidera à associer nombres et couleurs : on tourne dans un sens quand on augmente, dans l’autre quand on diminue.

Si on veut que le résultat final comporte beaucoup de couleurs, il faut tourner beaucoup dans le même sens (et même mieux : beaucoup dans un sens, puis beaucoup dans l’autre). Avant de tracer la courbe, il peut être bon de s’entraîner sur papier.

 

 

Un petit motif entièrement réalisé par une enfant de 6 ans

Hitomezashi

Un hitomezashi dans un cadre de taille 32 x 40 fait par 10 personnes (dont 4 enfants qui ont principalement couru autour de la fontaine) en 2h.

Lieu. Un espace avec un quadrillage carré qui peut être raffiné par la suite

Principe mathématique. Le hitomezashi est une forme de broderie traditionnelle japonaise qui suit des règles suivantes :

• on brode le long de chaque ligne (horizontale et verticale) d’un quadrillage de taille 1;
• l’aiguille passe dessus-dessous le tissu, en laissant les traits de longueur 1, avec des espaces de longueur 1 entre eux.

Le long de chaque ligne, en partant du bord, on a le choix de commencer le parcours soit en dessous soit au-dessus du tissu, ce qui se code avec un 0 ou un 1. Un morceau rectangulaire de tissu de taille n × m brodé en hitomezashi est entièrement codé par deux suites de 0 et de 1 : une pour le choix dans les lignes, et une pour les choix dans les colonnes. On obtient une broderie en lignes brisées qui soit se referment soit vont d’un bord à l’autre. Cette broderie est coloriable avec 2 couleurs de telle manière que les zones voisines ont des couleurs différentes.

L'avancement du dessin : coloriage du hitomezashi en cours, en continuant des traits verticaux.

Mise en place. D’abord, mettez en place une grille carrée en raffinant le quadrillage de la place. Un carré de base peut aller de 2 × 2 cm jusqu’à 5 ×5 cm. La grille peut s’agrandir avec l’avancement de l’activité en fonction du temps dont vous disposez et du nombre de participant·es.

Choisissez la manière à construire les deux suites de 0 et 1 qui définissent les traits horizontaux et verticaux. Quelques options :

1. (testée et appréciée) remplacez les voyelles par les 0 et les consonnes par les 1 : des suites de mots écrits sur les bords de la grille définiront alors la suite de 0 et de 1. Chacun et chacune peut écrire les lettres de son prénom par exemple sur un des bords, en accolant les prénoms les uns à la suite des autres;
2.  prenez un nombre irrationnel de votre choix et écrivez sa décomposition décimale en remplaçant les chiffres pairs par 0 et impairs par 1 (par exemple \(\pi\), \(e\), etc.)
3. prenez des suites périodiques en horizontal et en vertical : sans surprise, cela donnera une broderie périodique !

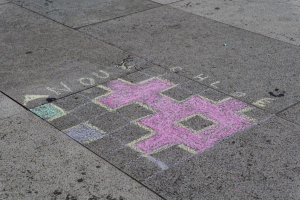
Déroulement.  Nous expliquons ici un déroulement de l’option 1. avec les prénoms. Proposez à quelques personnes d’écrire leurs prénoms sur un des bords du quadrillage. Il faut qu’il y ait des prénoms sur les deux bords, à partir du coin. Puis, chacune va broder les traits correspondants à chacune des lettres de son prénom (si besoin, en embauchant de l’aide). Il est très important de vérifier que les traits sont poursuivis jusqu’à assez loin et de ne pas laisser de trous entre les prénoms.

Vous pouvez colorier une partie qui s’est formée de votre hitomezashi en respectant les mêmes précautions que pour les pavages de Truchet (voir la partie Conseils pour les pavages de Truchet linéaires).