Aller de l’avant avec les problèmes inverses

Ne serait-il pas formidable d’avoir toutes les réponses ? Certes, mais encore faut-il connaître les questions… Imaginez que vous receviez un jeu de données, mais sans savoir précisément quelles conditions les ont produites, et que votre travail consiste précisément à déterminer ces conditions. C’est exactement ce que font tous les jours certains mathématiciens. Leur monde à l’envers est le domaine des problèmes inverses, et il prend tout son sens quand on réfléchit à la manière dont beaucoup de scientifiques et de médecins travaillent. En effet, comme en imagerie médicale ou dans les études sismiques, où nous savons ce qui sort de l’appareil d’IRM ou du sismographe, nombreux sont les domaines où nous devons remonter aux conditions initiales.

Ce domaine d’étude est actuellement en plein essor et trouve sans cesse de nouvelles applications. Ces trois derniers mois, des chercheurs en problèmes inverses venus du monde entier se sont réunis à L’Institut Henri Poincaré pour un trimestre intensif d’études, de discussions et de remue-méninges. Deux de ses organisateurs, Jérôme Le Rousseau, professeur à l’Université d’Orléans, et David Dos Santos Ferreira, professeur à l’Université de Lorraine, nous ont donné leur éclairage sur ces problèmes traités à rebours.

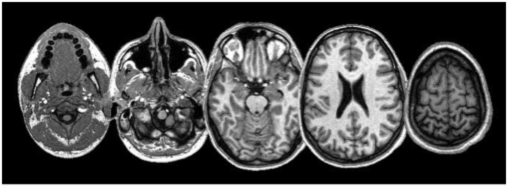
Image IRM du cerveau humain

Mais avant d’aller à l’envers, que signifie aller à l’endroit ? Si vous connaissez déjà les caractéristiques d’un système complexe donné, comme le corps humain ou la Terre, vous pouvez injecter des entrées, les paramètres de départ de votre scénario, et voir ce qui ressort. Par exemple, si le système défini est un modèle sismique, un mathématicien peut entrer les conditions données et simuler le séisme qu’elles produiraient.

Maintenant, imaginez que vous ne connaissiez pas votre système sous toutes les coutures. Il peut s’agir d’un patient chez qui l’on recherche des tumeurs internes ou d’une région géologique où l’on souhaite déterminer l’emplacement du magma sous la surface terrestre afin d’évaluer le risque d’activité volcanique. Dans un cas comme dans l’autre, vous cherchez à voir ce qu’il se passe à l’intérieur, mais sans pouvoir creuser un trou et éclairer avec votre lampe torche. Ce qui est en revanche possible, c’est d’envoyer des ondes d’énergie à travers la surface ou le corps et regarder comment elles se comportent. La manière dont leur trajectoire initiale est modifiée, ralentie ou déviée nous renseigne sur le matériau qu’elles ont traversé. Cette fois, les nombres avec lesquels vous devez travailler sont les résultats enregistrés quand ces ondes ressortent de l’autre côté, et non le point de départ. Quelles étaient donc les conditions qui ont produit ces résultats ? Savoir répondre à cette question, c’est être capable de reconstruire la structure du rein qui disperse les ondes exactement comme l’a détecté l’appareil d’IRM, ou les composants de la Terre sous vos pieds. C’est un problème que l’on résout à l’envers : un problème inverse.

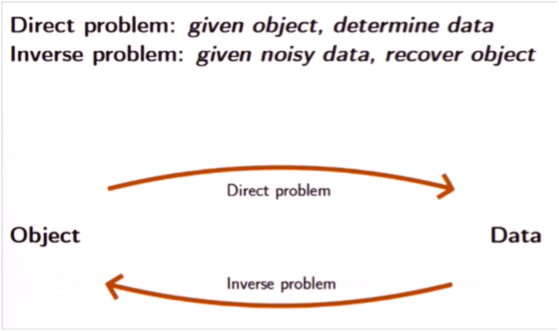
Problème direct : étant donné un objet, déterminer les données Problème inverse : étant donné des données bruitées, retrouver l’objet (S. Siltanen)

Retrouver l’intégralité de la présentation donnée par S. Siltanen lors de l’école d’initiation au début du trimestre.

Toujours plus loin avec les problèmes inverses

Cette branche des mathématiques a donc ouvert la voie à de nouvelles techniques dans toutes sortes de domaines, comme l’exploration pétrolière et gazière ou les prévisions météorologiques. Les mathématiciens spécialistes des problèmes inverses continuent à les améliorer, rendant ces techniques plus fiables, plus précises, ou plus sûres pour les patients. Revenons à l’exemple de l’imagerie médicale. La sécurité des patients présente une limite majeure à la résolution qui peut être obtenue dans les divers types d’images car leur exposition aux ondes énergétiques ne doit pas dépasser une certaine limite. Comment les mathématiques peuvent-elles contourner cette contrainte physique élémentaire ? « C’est une question que les mathématiciens abordent naturellement dans leur travail, explique J. Le Rousseau. Ils se demandent ’’Si je réduis mes données, perd-on en résolution ? Perd-on en qualité ?’’ » S’ils réussissent à adapter leurs méthodes à des données plus réduites tout en répondant par la négative à ces questions, cela permettrait d’envisager des examens plus courts pour obtenir le même résultat, ce qui signifie moins d’exposition aux rayons X pour les patients.

Ce principe a par exemple débouché sur une application pratique dans le fauteuil du dentiste. Pour vous poser des implants dentaires, le dentiste doit creuser la mâchoire, où se trouvent des nerfs auxquels vous ne voulez surtout pas toucher, mais qui ne se situent pas exactement au même endroit pour tout le monde. En travaillant avec des dentistes et des ingénieurs, les spécialistes des problèmes inverses ont contribué à fournir de meilleurs résultats d’imagerie pour la localisation des nerfs, tout en maintenant au plus bas l’exposition aux rayons X.

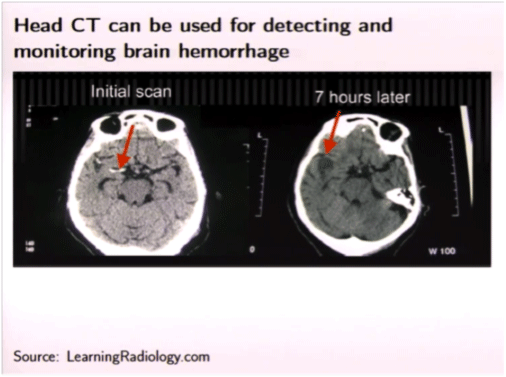
Un tomodensitogramme de la tête peut être utilisé pour détecter une hémorragie cérébrale et suivre son évolution (S. Siltanen)

Si ces applications de pointe sont une nouveauté, ce n’est pas le cas des problèmes inverses. « Ils sont aussi vieux que l’humanité. Les mesures indirectes étaient déjà utilisées par les Grecs anciens pour accéder à des quantités physiques « impossibles à mesurer » : Ératosthène a par exemple utilisé la longueur des ombres pour estimer la circonférence de la Terre, explique D. Dos Santos Ferreira. À partir du moment où vous dites ’’Je n’ai pas accès à la bonne mesure, mais je trouverai la réponse par d’autres moyens’’, vous utilisez une approche de problème inverse. » Les applications actuelles des problèmes inverses mettent cependant en lumière la relation intime entre la recherche mathématique pure et dure et des usages tout à fait familiers, voire essentiels.

Pour poursuivre ces avancées réalisées grâce aux problèmes inverses, J. Le Rousseau souligne à la fois l’importance d’investir dans la recherche, et ce sans en attendre des résultats concrets immédiats, et le besoin crucial de liberté scientifique. Pour lui, c’est cette dernière qui rend en effet possible la créativité, un ingrédient fondamental de la recherche et de l’innovation. L’IHP, hôte du trimestre consacré aux problèmes inverses, est un lieu renommé pour offrir cette liberté académique. D. Dos Santos Ferreira souligne le caractère enrichissant des échanges entre disciplines, comme lorsqu’un groupe de géophysiciens est venu échanger avec les mathématiciens réunis : « Ces interactions apportent des idées et des méthodes nouvelles. Les autres disciplines nourrissent notre recherche tout en nous laissant rester des mathématiciens. »

Pour en savoir plus

Communiquez avec les chercheurs de la communauté des problèmes inverses et découvrez leur travail plus en détail, sur la plateforme Polaris de l’IHP.

Une courte introduction aux problèmes inverses et le programme de l’Institut Henri Poincaré, avec Colin Guillarmou, co-organisateur.

La présentation de Gunther Uhlmann, Harry Potter’s Cloak, sur une autre application des problèmes inverses : métamatériaux et capes d’invisibilité (en anglais).

Calcul de la circonférence de la Terre par Ératosthène.