L'effet Dimdim
L’algorithme de Dimitri est le suivant :
- Effacer l’ardoise
- Ecrire un nombre entier sur l’ardoise.
- Le multiplier par 7 puis ajouter 3 et noter le résultat sur une feuille.
- Reprendre le nombre de départ et cette fois :
- Le multiplier par 2 puis soustraire 7 et noter ce résultat sur la feuille.
- Diviser le premier nombre écrit sur la feuille par le deuxième.
- Ecrire le résultat sur l’ardoise.
A sa grande surprise, Dimitri constate qu’en appliquant son algorithme au résultat obtenu, il retrouve le nombre de départ. Il s’exclame alors : « C’est de la sorrrcellerrrrie ! Je peux réussirrrr à deviner le nombrrrre effacé en calculant le rrrrésultat du rrrrésultat ! » . Pouvez-vous reformuler les paroles de Dimitri puis expliquer en quoi le phénomène n’a rien de magique ?
Solution
Appelons \(A\) le nombre écrit au départ sur l’ardoise.
A l’issue de l’algorithme de Dimitri, le nombre écrit sur l’ardoise est \(\frac{7A+3}{2A-7}\).
L’explication tient à l’équivalence \(B=\frac{7A+3}{2A-7} \Leftrightarrow \frac{7B+3}{2B-7}=A\).
Pour aller plus loin
Les deux résultats écrits sur la feuille s’obtiennent à partir du nombre de départ par une multiplication par un nombre fixé et une addition d’un (autre) nombre fixé. Le résultat final s’obtient en divisant ces deux résultats intermédiaires l’un par l’autre.
Pouvez-vous trouver tous les algorithmes calqués sur ce même schéma, et ayant l’effet Dimdim c’est-à-dire, les algorithmes ayant le même effet dans les deux sens?
De tels algorithmes, transforment un nombre \(A\) en un nombre \(B=\frac{aA+b}{cA+d}\) où \(a,b,c\) et \(d\) sont des nombres réels.
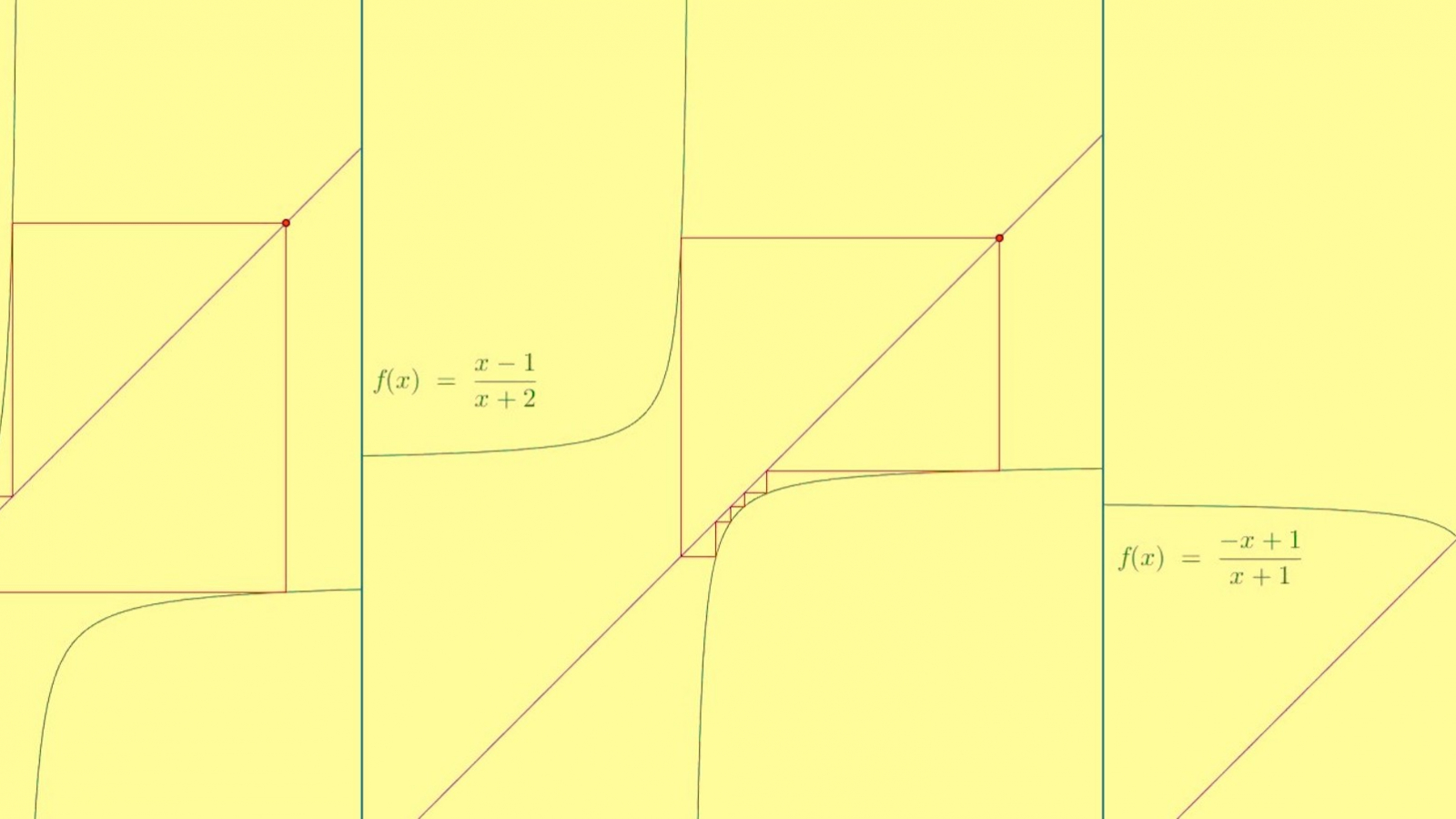
Nous verrons dans un prochain billet que le nombre \(B\) redonnera le nombre \(A\) par le même algorithme lorsque \(a+d=0\). Nous aurons besoin pour expliquer ceci, de quelques outils supplémentaires. Mais d’abord, il nous faut mieux comprendre ces algorithmes d’un type si particulier. Regardons un autre exemple.
De l'Or, seulement de l'Or !
Anastasia, la sœur de Dimitri, affectionne tout particulièrement le nombre d’or. Le nombre d’or est égal à \(\frac{1+\sqrt 5}{2}\). Anastasia utilise le nombre d’or dans l’algorithme suivant :
- Effacer l’ardoise.
- Ecrire un nombre entier sur l’ardoise.
- Ajouter le nombre d’or.
- Prendre l’inverse.
- Prendre l’opposé.
- Ecrire le résultat sur l’ardoise.
Elle a constaté, après plusieurs essais, qu’appliquant son algorithme à un nombre, puis en réappliquant son algorithme au résultat et en répétant plusieurs fois, elle retrouvait toujours le nombre de départ.
Combien de fois, au minimum, Anastasia a-t-elle répété son algorithme ?
Solution
Anastasia a répété son algorithme 10 fois au minimum. Expliquons pourquoi.
Partant d’un nombre \(A\), l’algorithme d’Anastasia produit le nombre \(\frac{{ – 1}}{{A + \phi }}\).
En observant les répétitions de l’algorithme d’Anastasia, on remarque qu’après la cinquième répétition, le nombre produit est \(- A\). Les calculs pour y arriver peuvent être simplifiés en tenant compte de l’égalité suivante satisfaite par le nombre d’or : \(\phi^2 = \phi + 1\).
Par conséquent, en appliquant cinq fois de plus (dix fois en tout) son algorithme, Anastasia retrouvera le nombre dont elle est partie.
ÉCRIT PAR
Sébastien Kernivinen
Enseignant en mathématiques - CNED, Rennes.
