
Défi de la semaine
On veut colorier les cases d’une grille de dimensions \(4×4\) en blanc et noir, de sorte qu’il y ait exactement deux cases noires et deux cases blanches dans chaque ligne et chaque colonne. Combien de manières de faire existe-t-il pour cela ?


Solution du 1er défi d'avril 2024
La réponse est 1013.
Si \(n=1013\), on a \(2^{2024}+2^{1013}+1=(2^{1012}+1)^2\).
Si \(n<1013\), on a :
\[
(2^{1012})^2 < 2^{2024}+2^n+1 < 2^{2024}+2^{1013}+1=(2^{1012}+1)^2.
\]
Donc, pour les valeurs entières de \(n\) telles que \(n<1013\), le nombre \(2^{2024}+2^n+1\) est strictement compris entre les carrés de deux entiers consécutifs et n’est donc pas un carré. Ainsi, la plus petite valeur de \(n\) permettant que le nombre soit un carré parfait est \(n=1013\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock





21h59
Si on considère que la grille est fixe ( un échiquier avec la case blanche à droite est différent d’un échiquier avec la case noire à droite) il y a 36 possibilités.
On choisis deux cases noires sur la première ligne ( 6 possibilités ) puis sur la seconde ( 6 possibilités ) et on complète la grille avec les deux dernières lignes, il y a toujours une unique possibilité.
7h08
Non il peut rester plusieurs possibilités une fois coloriées les \(2\) premières lignes. Exemple :
\(NBBN\)
\(BNBN\)
\(BNNB\)
\(NBNB\)
On obtient une autre solution juste en permutant les \(2\) dernières lignes :
\(NBBN\)
\(BNBN\)
\(NBNB\)
\(BNNB\)
6h52
On remarque qu’à tout coloriage valide de la grille correspond un autre coloriage valide obtenu en permutant les couleurs. On peut donc compter les solutions avec la case \((1,1)\) en noir, et il suffit de multiplier par \(2\) pour avoir le nombre total de solutions.
On a alors \(3\) possibilités pour choisir la seconde case noire \((1,j)\) dans la ligne \(1\), et \(3\) pour choisir la seconde case noire \((i,1)\) dans la colonne \(1\), soit \(3 \times 3 = 9\) possibilités de colorier la ligne \(1\) et la colonne \(1\).
On doit choisir ensuite la couleur de \((i,j)\) :
Blanc : il reste \(2\) possibilités pour la seconde case noire \((i,j’)\) dans la ligne \(i\), et \(2\) possibilités pour la seconde case noire \((i’,j)\) dans la colonne \(j\), soit \(2 \times 2 = 4\) façons de colorier la ligne \(i\) et la colonne \(j\). On a alors colorié entièrement \(2\) lignes et \(2\) colonnes, soit \(12\) cases sur \(16\), dont \(5\) en noir sur \(8\) requises. Il reste donc à choisir l’unique case blanche parmi les \(4\) restantes, mais c’est forcément \((i’,j’)\) sinon il y aurait \(3\) cases noires dans la ligne \(i’\) ou la colonne \(j’\).
Noir : on colorie en blanc le reste de la ligne \(i\) et de la colonne \(j\). On a alors \(12\) cases coloriées dont \(4\) en noir, donc les \(4\) restantes seront noires.
Le nombre total de coloriages valides de la grille est donc \(2 \times 9 \times (4 + 1) = 90\).
14h06
Les colonnes auxquelles appartiennent les deux cases noires de la première ligne ont chacune une autre case noire parmi les trois autres lignes. Il existe donc au moins une ligne dont les cases noires ne partagent pas les mêmes colonnes que celles de la première ligne.
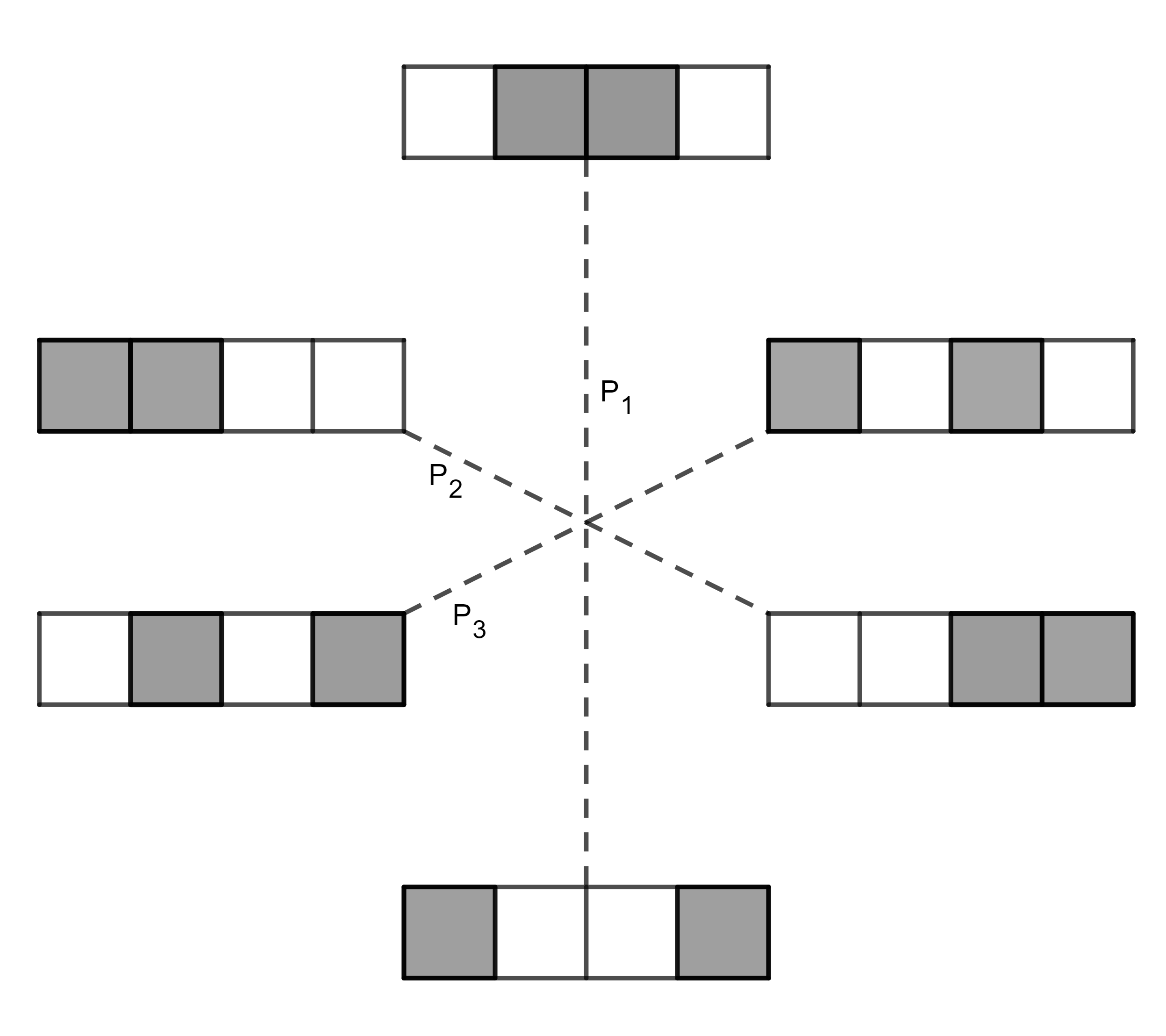
Chaque grille est donc composée de deux paires de lignes dont les cases noires appartiennent à des colonnes différentes. Il y a trois paires de ce type notée \(P_1\), \(P_2\) et \(P_3\) sur le document joint.
Si les paires sont différentes , il y a \(4\times3\times2=24\) façons de choisir l’ordre des lignes.
Si elles sont identiques, il y a \(2\times 3=6\) façons de choisir l’ordre des lignes.
Finalement, il existe \(3\times24+3\times6=90\) grilles possibles.
11h41
Une suite de cases blanches et noires peut être comparée à suite de 0 et de 1, et par conséquent à une suite de nombres représentés en binaire.
En l’occurrence, nous avons 4 nombres consécutifs constitués chacun par quatre bits, un par ligne. (On aurait pu aussi constituer un plus grand nombre à 16 bits et travailler sur des indices de tableau).
Nous utilisons les nombre suivants :
0011 3
0101 5
0110 6
1001 9
1010 10
1100 12
Puisque chaque colonne et chaque ligne doit compter deux bits à 1 (deux cases noires ou deux cases blanches, selon votre choix), chaque somme de ligne ou colonne s’élèvera à : 2 * 8 + 2 * 4 + 2 * 2 + 2 * 1 = 30.
Le problème consiste alors à choisir dans la liste de nombres ci-dessus, quatre d’entre eux (au plus deux de chaque) afin d’atteindre la somme de 30.
Exemple :
0011 3
0011 3
1100 12
1100 12
Le fait est que l’addition à la verticale est alors aussi correcte, et compte à chaque fois deux bits à 1, et que leur somme verticale fait également 30.
Je vous fais grâce de la recherche elle-même de chaque solution, mais on en trouve bien 90, évidemment, comme cela a déjà été démontré.