J’ai toujours aimé les bestiaires. Peut-être parce qu’ils nous retournent l’image – souvent déformée – de chaque époque. Aujourd’hui, nous mathématiciens, nous pouvons déjà percevoir l’image – possiblement déformée – des mathématiques du XXIème siècle.
Il y a quelques mois, alors que je préparais un autre billet, je suis tombé par hasard sur le site Visualizar’09 : Datos Públicos, Datos en público. Là-dedans, un lien a attiré toute de suite mon attention : Bestiario.
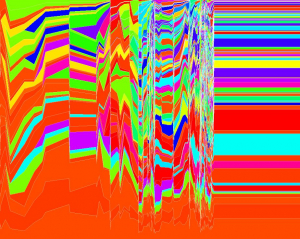
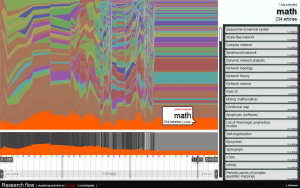
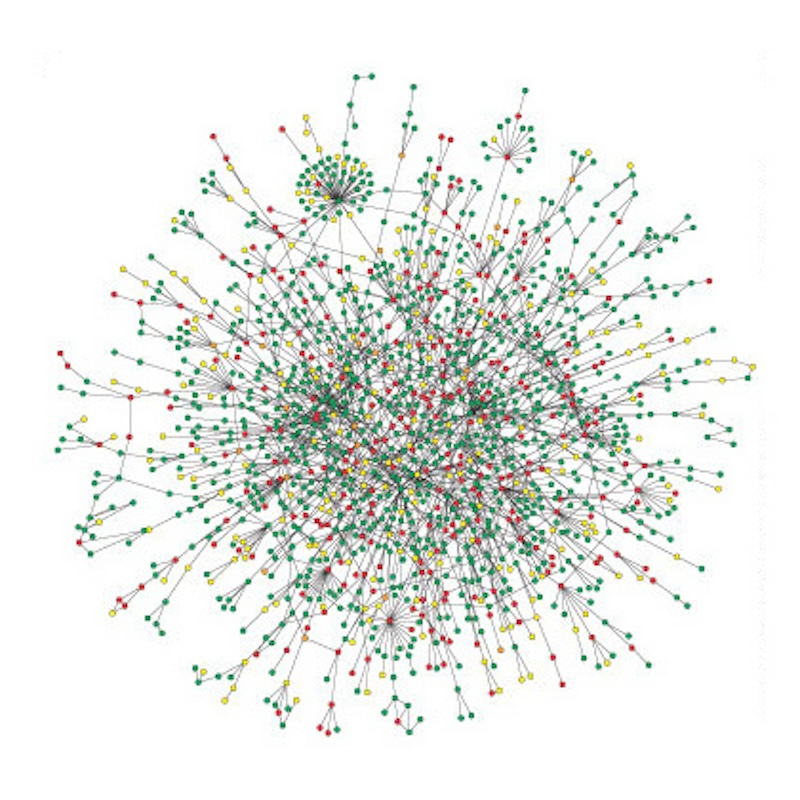
C’est un bestiaire nouveau avec quelques jolies bêtes. Je voudrais parler ici de l’une de ces bêtes, appelée « flow », à savoir le flot d’articles de Wikipédia utilisés par les responsables du site. Ils sont des entrepreneurs, des économistes, des artistes, des architectes, des ingénieurs, même des mathématiciens, réunis dans une compagnie qui veut « rendre compréhensible la complexité ».
.
On dira que ce flot est bien moins intéressant que celui des publications sérieuses où le rôle des mathématiques semble beaucoup plus petit [voir encart].
Mais à mon avis ce qui rend intéressante cette image, c’est justement qu’on y voit le goût pour les mathématiques et pour la géométrie de gens qui ne sont pas des mathématiciens ou des scientifiques. Et on entrevoit aussi que les sciences de la vie, en un sens large, ont déjà remplacé les sciences de la matière comme moteur des mathématiques nouvelles.
.
Encart
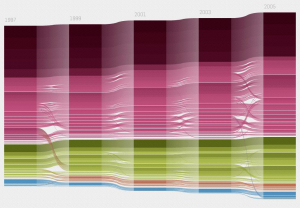
Voici le flot temporel de l’influence des plus importantes publications scientifiques, où les mathématiques font partie du petit ruban bleu. Chaque revue est représentée par une courbe dont l’épaisseur est proportionnelle à son importance, mesurée par une quantité appelée Eigenfactor™.
Ces courbes sont groupées en agrégats, liés par les citations mutuelles, semblables à des arbres avec des branches et des racines thématiques de couleurs différentes. Je regrette quand même qu’on n’ait pas comparé la vie
moyenne des articles, ce qui entraînerait probablement l’élagage de quelques jolies branches roses et vertes.
.
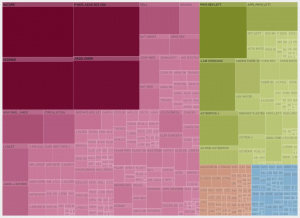
On peut aussi représenter les revues par des rectangles emboîtés dans une portion rectangulaire du plan. L’aire de chaque rectangle est proportionnelle à l’importance de la revue, mesurée encore par son Eigenfactor™. On connaît cette représentation par son nom anglais
« treemap ».
Quand on clique sur une revue, on voit apparaître son flot de citations (comme celui de la revue Annals of Mathematics) où les flèches blanches représentent les citations entrantes, celles noires les citations sortantes et la longueur des flèches donne la mesure du nombre de citations.
.
.
Pour mieux comprendre les difficultés que comporte le fait de vouloir mesurer, puis comparer l’activité scientifique, je recommande la lecture du rapport Citations Statistics de Robert Adler, John Ewing et Peter Taylor et des articles de Fabrice Planchon et de Jean-Marc Schlenker dans ce site.
ÉCRIT PAR
Fernando Alcalde Cuesta
Professeur - Université de Saint Jacques de Compostelle (Espagne)
