Connaissez-vous ce livre de Roger Nelsen ?
Preuves sans mots
Quelle que soit votre réponse, je vous prie de vous concentrer sur la figure dessinée sur la couverture. Elle illustre la preuve contemplative standard du fait que la somme des \(n\) premiers nombres impairs \(1, 3, 5, …, 2n-1\) est égale à \(n^2\). Elle consiste à imaginer que le grand carré est obtenu à la \(n\)-ème étape d’une sorte de processus de croissance cristalline. Ce processus part du carreau situé au coin en bas à gauche, représenté par un petit disque rouge sur la couverture du livre. Chaque étape ajoute une nouvelle couche de carreaux le long des côtés droits et supérieurs du cristal obtenu à l’étape précédente. Ces couches sont successivement représentées par des disques noirs ou rouges situés à l’intérieur de leurs carreaux.
Le nombre total de carreaux est d’une part égal à \(n^2\), car les côtés du grand carré sont partagés en \(n\) parties égales. Mais d’autre part, ce nombre est aussi égal à la somme des nombres de carreaux dans chaque couche. Ces nombres sont précisément les \(n\) premiers nombres impairs \(1, 3, 5, …, 2n -1\).
————
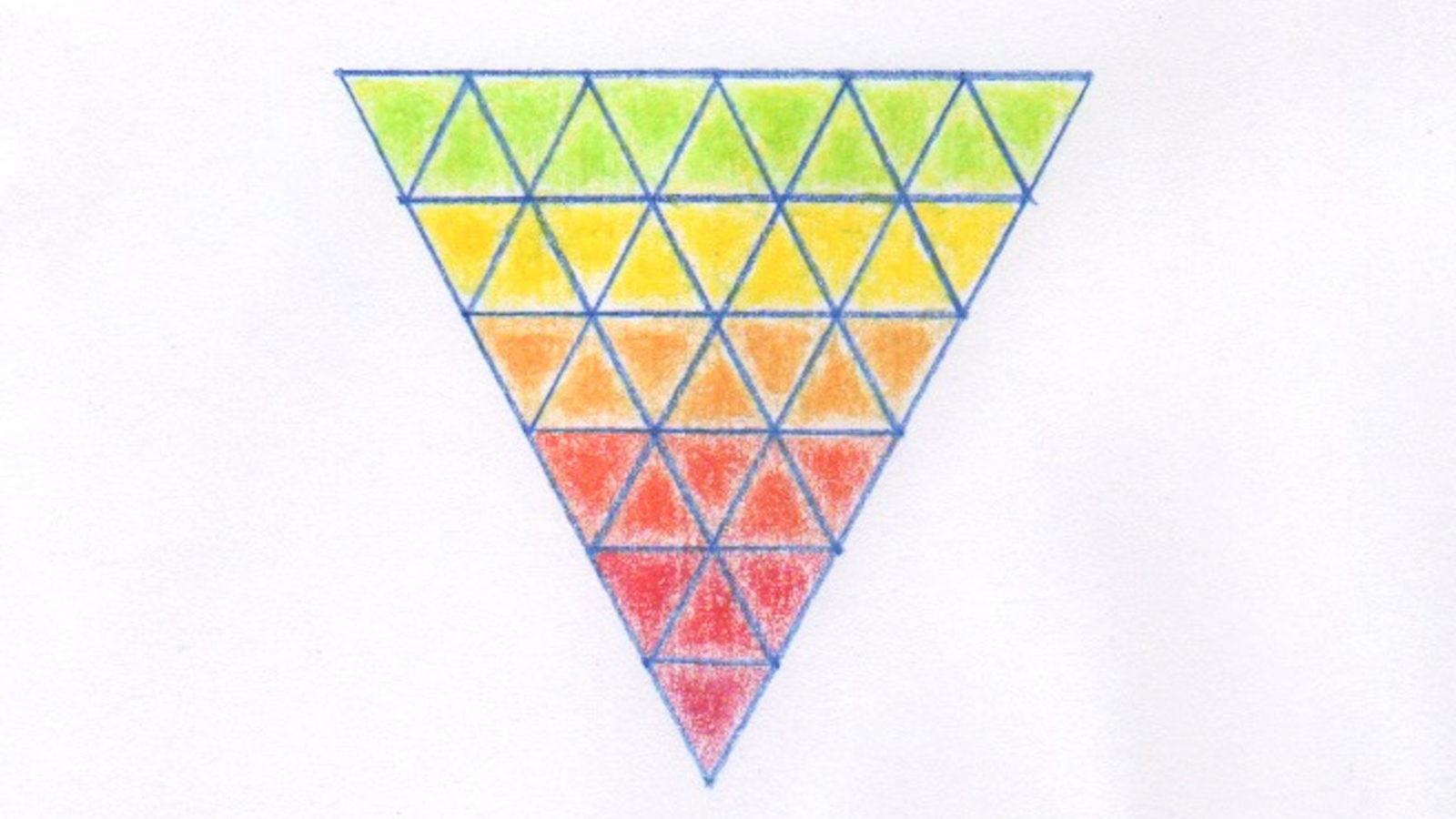
Regardez maintenant le logo de cet article. On y voit cette fois-ci un triangle équilatéral dont chaque côté est partagé en \(n\) parties égales. En joignant les points de partage par des segments parallèles aux côtés, le grand triangle se trouve décomposé en copies plus petites de lui-même, toutes de même taille. Comptons les mini triangles situés dans les bandes formées par deux segments parallèles successifs, en partant de l’une des pointes du grand triangle. On trouve de nouveau les \(n\) premiers nombres impairs !
Est-il possible d’obtenir ainsi une seconde preuve contemplative de l’identité \(1 + 3 + \dots + (2n-1) = n^2\) ? Pour cela, il faudrait arriver à voir sans calculs que le grand triangle contient exactement \(n^2\) mini triangles. Y arrivez-vous ?
Si vous avez réussi, je vous félicite ! Sinon, alors contemplez cette figure, tirée du même livre de Roger Nelsen, et proposée initialement par Jeno Lehel 3Il proposa cette preuve visuelle à la page 103 de Mathematics Magazine {{64}}, No. 2 (1991).:
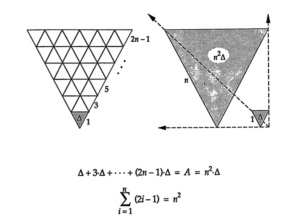
Figure
Explication
L’idée est de calculer de deux manières différentes l'{aire} \(A\) du grand triangle en fonction de l’aire \(\Delta\) de l’un des mini triangles équilatéraux qui le composent.
À gauche, cette aire est obtenue comme somme des aires des bandes. Mais celles-ci contiennent successivement \(1, 3, …, 2n-1\) mini triangles. On obtient donc l’égalité de gauche \(\Delta + 3 \cdot \Delta + \cdots + (2n-1) \cdot \Delta = A\).
À droite, on constate que le grand triangle s’obtient à partir du petit par une dilatation (aussi appelée {homothétie} par les mathématiciens) de rapport \(n\). Son aire est donc dilatée par le facteur \(n^2\), ce qui explique l’égalité de droite \(A = n^2 \cdot \Delta\).
On conclut en combinant les deux égalités et en simplifiant par \(\Delta\).
Comprendre cette preuve me produisit un frisson de plaisir. C’est pour partager avec vous ce frisson que j’ai écrit cette tribune. Je n’avais jamais relié l’identité arithmétique ci-dessus à la propriété géométrique fondamentale disant qu'{une dilatation de rapport \(n\) de n’importe quelle figure géométrique plane multiplie son aire par \(n^2\)} 4Cette propriété des dilatations permet aussi de prouver le théorème de Pythagore, expliquant ainsi pourquoi ce sont des nombres élevés au carré qui y tiennent les rôles clés. Serge Cantat et Andrés Navas ont expliqué de telles preuves dans leurs articles Pythagore et les courbes de Pólya et Encore une preuve du théorème de Pythagore. !
ÉCRIT PAR
Patrick Popescu-Pampu
Professeur - Université de Lille
