« Une question, un chercheur », c’est un cycle de conférences organisé conjointement par la Société Française de Physique (SFP), la Société Mathématique de France (SMF), l’Union des Professeurs de Spéciales (UPS) et l’Institut Henri Poincaré (IHP). Alternativement, un physicien et un mathématicien s’adressent à un public d’élèves des classes préparatoires aux grandes écoles et des licences universitaires. Après le physicien Michel Spiro en décembre dernier, c’était le tour de Laure Saint-Raymond le 31 mai 2013. Il était question d’océanographie. On était en plein dans les Mathématiques pour la Planète Terre (MPT).
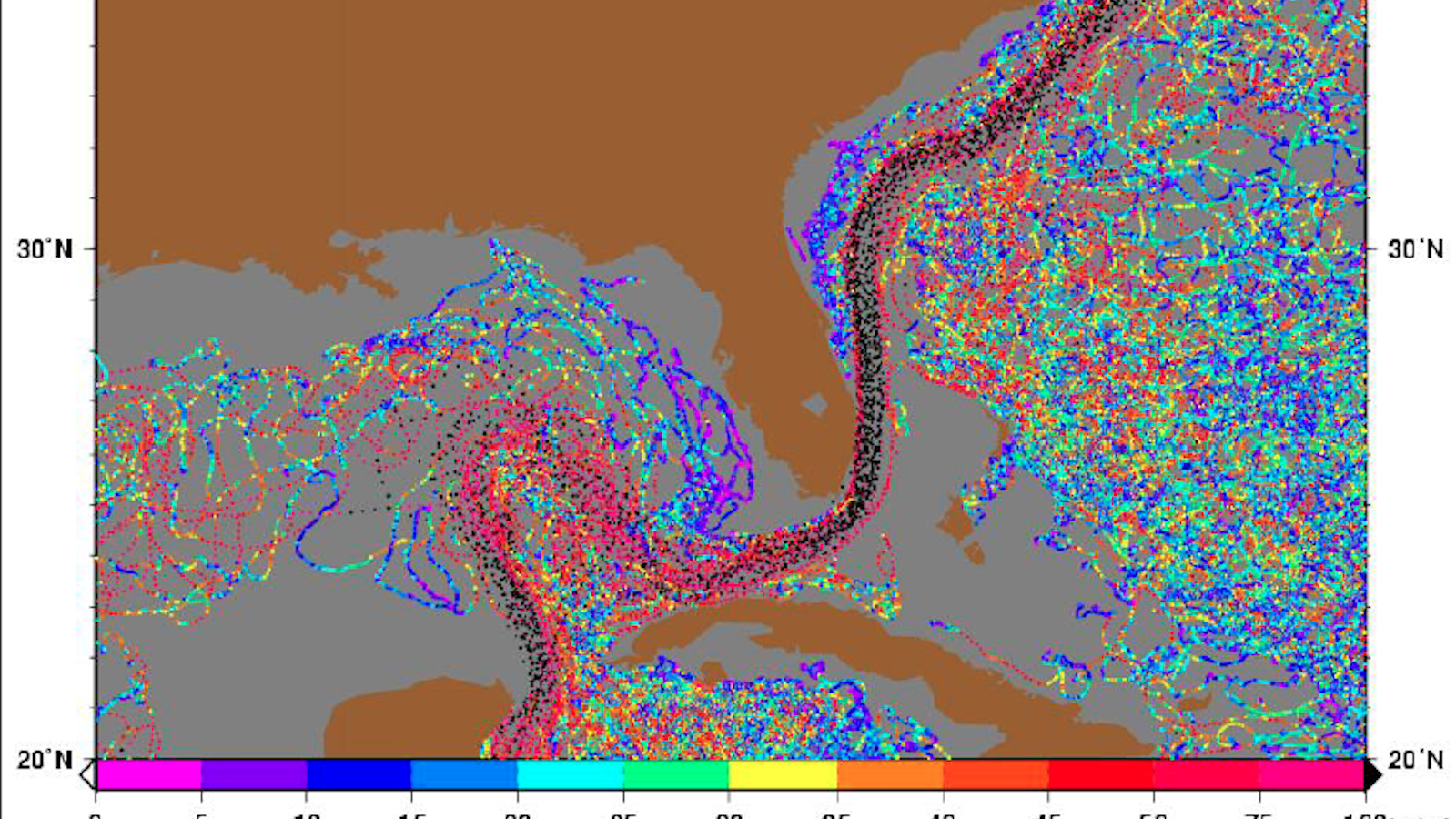
La carte des courants dans l’Atlantique Nord n’est pas du tout symétrique : le Gulf Stream crève les yeux. Courant violent et concentré dans une bande étroite, il épouse la côte américaine à partir de la Floride, puis décroche au cap Hatteras pour poursuivre sa route plein ouest. Rien de similaire en face de l’Amérique, le long des côtes d’Europe ou d’Afrique. Laure Saint-Raymond propose une explication mathématique à ce phénomène à la fois spectaculaire et d’une importance cruciale pour les conditions de vie en Europe occidentale.
Dans le modèle simplifié qu’elle traite, l’océan est ramené à une crêpe 2-dimensionnelle homogène et incompressible. On prend en compte la viscosité (faible, même si on la corrige pour tenir compte grossièrement de la turbulence), l’accélération de Coriolis (liée à la rotation de la Terre) et la force exercée par le vent, incluse dans un terme de forçage. On obtient un système de deux équations différentielles linéaires du second ordre (l’inconnue est un champ de vecteurs, la vitesse du courant en chaque point), qui s’écrit
Coriolis + pression – \(\nu\times\) viscosité = forçage,
couplé à une troisième équation, qui exprime l’incompressibilité. La condition aux limites est l’annulation des deux composantes de la vitesse le long du bord.
On considère le coefficient de viscosité turbulente \(\nu\) comme un petit paramètre qu’on fait tendre vers 0. C’est le comportement asymptotique des solutions lorsque \(\nu\) tend vers 0 qui nous intéresse.
La première chose à faire est d’étudier l’équation limite obtenue en faisant \(\nu = 0\), appelée équation de Sverdrup. Elle est d’ordre inférieur car c’est justement dans la viscosité que figurent les dérivées d’ordre le plus élevé. Après un
changement de fonction inconnue,
D’après le Lemme de Poincaré, un champ de vecteurs de divergence nulle est le rotationnel (gradient tourné de 90°) d’une fonction scalaire \(\psi\), appelée fonction de courant, unique à une constante additive près. On se ramène à une équation aux dérivées partielles d’inconnue \(\psi\), de la forme
Coriolis – \(\nu\times\) viscosité = forçage.
Au bord, \(\psi\) et sa dérivée normale s’annulent.
Dans cette équation, Coriolis désigne la dérivée de \(\psi\) le long des parallèles, c’est un terme de transport (en réalité, il ne s’agit que d’un terme du second ordre, le terme principal dans l’accélération de Coriolis, celui été obtenu en approximant la Terre par un plan, ayant été absorbé par le gradient de pression). La viscosité est le bilaplacien (laplacien itéré, un opérateur d’ordre 4) de \(\psi\), multipliée par une constante physique \(\nu\), la viscosité turbulente, considérée comme petite. On s’intéresse au comportement asymptotique des solutions lorsque ce paramètre tend vers 0. Il s’agit d’une limite singulière, puisque, dans le cas où la viscosité turbulente vaut 0, l’ordre de l’équation (appelée équation de Sverdrup) chute de 4 à 1.
elle s’apparente à une équation de diffusion (analogue à l’équation de la chaleur) dans laquelle le rôle du temps est joué par la longitude (la dérivée par rapport à la longitude est cachée dans la force de Coriolis).
On sait depuis Fourier que pour ces équations, le sens du temps n’est pas anodin : à peu près n’importe quelle distribution initiale de température peut évoluer selon l’équation de la chaleur, et, lorsque le temps s’écoule, la température devient très régulière. Inversement, on ne peut remonter le temps qu’en partant d’une distribution de température très régulière. Autrement dit, pour une équation de diffusion, on ne peut imposer une condition aux limites que d’un seul côté : pour l’équation de la chaleur, c’est au début de l’intervalle de temps considéré ; pour l’équation de Sverdrup, c’est le long des côtes situées à l’est de l’océan, i.e., l’Europe et l’Afrique. Cela indique que, lorsque \(\nu\) tend vers 0,
une discontinuité se produit.
Pour simplifier encore, supposons que l’océan est une bande infinie orientée Nord-Sud, et que le forçage et la fonction de courant \(\psi\) ne dépendent que de la longitude. On est ramené à une équation différentielle ordinaire. L’équation limite, celle où la viscosité turbulente \(\nu\) est posée égale à 0, est la plus simple qui soit : la dérivée de \(\psi\) doit être égale au forçage (le vent !). En général, aucune solution ne peut satisfaire les conditions aux limites (l’intégrale du vent n’a aucune raison d’être nulle). Pourtant, une estimation d’énergie (résultant d’une simple intégration par parties) montre que les solutions \(\psi_{\nu}\) sont bornées en norme \(L^2\), indépendamment du petit paramètre \(\nu\). Lorsque \(\nu\) tend vers \(0\), elles convergent, mais vers une fonction discontinue. Cela indique que le champ des vitesses, qui est une dérivée de \(\psi_{\nu}\), devient très grand quelque part.
En faisant brutalement \(\nu=0\), on a fait une bêtise, qu’il s’agit maintenant de rattraper. Lorsque \(\nu\) est petit et non nul, les solutions parviennent à partir de 0 en Amérique pour arriver à 0 en Afrique. Comment ? Depuis le début du XXème siècle (Prandtl), on sait qu’il se forme une couche limite : on peut traiter séparément la région éloignée du bord, vérifiant une condition de non-pénétration, et une couche étroite localisée dans un voisinage du bord (couche limite). Loin du bord, l’équation de Sverdrup est satisfaisante. Dans la couche limite, les effets visqueux dominent.
Le raccord permet de satisfaire les conditions aux limites.
Pour l’océan unidimensionnel, la méthode consiste à ajouter une correction \(\psi_{cl}\) à \(\psi\), concentrée au voisinage du bord, et sujette à l’équation homogène
Coriolis – \(\nu\times\) viscosité = 0,
en considérant que la viscosité doit dominer. Exprimée en fonction de la dérivée \(\phi=\psi’_{cl}\), l’équation est \(\phi-\phi »’=0\). Les solutions sont des combinaisons linéaires d’exponentielles dont les exposants sont les racines du polynôme caractéristique, i.e. les racines cubiques de l’unité. A l’extrémité ouest de l’océan (unidimensionnel), la racine 1 donne une solution rapidement croissante, donc à éliminer. A l’extrémité est, ce sont les deux autres racines qu’on doit éliminer. Il y a donc deux solutions rapidement décroissantes à l’ouest, ce qui permet d’ajuster la condition au bord, alors qu’à l’est, la condition au bord détermine uniquement la solution. La solution réelle est une combinaison de la solution \(\psi\) de l’équation de Sverdrup et de \(\psi_{cl}\), sa dérivée (et donc le champ des vitesses) est grande uniquement le long du bord ouest.
En océanographie, cette méthode de développement multi-échelle a été appliquée avec succès dès 1905 pour expliquer un phénomène observé par l’explorateur polaire Nansen : en dérivant, les icebergs font un angle de 30 à 40° par rapport à la direction du vent. Ekman a pu montrer que la direction du courant variait rapidement en fonction de la profondeur au voisinage de la surface, ce qui a été établi mathématiquement depuis. La méthode s’applique aussi à la dynamique globale bidimensionnelle de l’océan Atlantique : la couche limite, où la vitesse est très grande, c’est le Gulf Stream le long de la Floride.
Les physiciens l’ont compris depuis belle lurette. Les mathématiques permettent de faire un pas de plus dans la prise en compte de la forme des côtes. Dans un océan modèle où la côte ouest a une forme suffisamment contournée pour devenir tangente à un parallèle, on peut démontrer mathématiquement que la couche limite se prolonge le long du parallèle jusqu’à la côte opposée (c’est un tour de force d’analyse). C’est conforme au comportement du Gulf Stream qui décroche de la côte américaine au Cap Hatteras, là où elle s’incurve le plus vers l’est.
Ces progrès mathématiques permettent d’envisager, pour l’avenir, la prise en compte de davantage de facteurs, comme la température, véritable moteur de l’océan (insuffisamment comprise physiquement), et le relief sous-marin.
Au-delà de ce bref résumé, l’exposé enchaînait des raisonnements simples (donc certains figurent dans les encadrés, recommandés en seconde lecture) et des analogies qui sont le fil conducteur de la pensée du spécialiste en équations aux dérivées partielles. On avait l’impression de toucher du doigt l’intuition du mathématicien confronté à un problème ardu mais motivant.
Ce soir-là, dans l’amphi Hermite, il y avait indubitablement un chercheur (enfin, une chercheuse) de grand talent. Quelle était la question du jour ? Difficile à choisir, car les questions ont fusé, à la fois des questions techniques sur les détails de l’exposé, car le public n’a pas décroché une seconde, et des questions plus générales sur le rôle des mathématiques et des mathématicien-ne-s dans cette aventure commune avec la physique et les sciences de la Terre. Mais il y a tout de même eu une question particulièrement bien sentie, une vraie colle : que se passe t’il dans l’hémisphère sud ? Voici la réponse : C’est toujours à l’ouest qu’on rencontre les courants resserrés et violents. La raison est que la force de Coriolis dépend de la dérivée par rapport à la latitude de la composante verticale de la vitesse de rotation, qui ne change pas de signe lorsqu’on traverse l’équateur. Toujours plus à l’ouest, disait le professeur Tryphon Tournesol.
ÉCRIT PAR
Pierre Pansu
Professeur - Université Paris-Saclay
