Courbe équicordale

Les courbes équicordales constituent une autre classe de courbes planes remarquables presque oubliées ou à peine connues, à l’instar des catoptrices.

Soit \(C\) une courbe de Jordan, i.e. une courbe plane simple fermée (Une courbe de Jordan est l’image d’une application continue \(\varphi \) de l’intervalle \([0,1]\) dans le plan telle que \(\varphi (0) = \varphi (1)\) et telle que la restriction de \(\varphi \) à l’intervalle ouvert \((0,1)\) soit injective). Un point intérieur à \(C\) est dit équicordal par rapport à \(C\) si toutes les cordes contenant ce point (cordes spécifiques) ont la même longueur.

Une courbe plane fermée ayant un point équicordal est dite équicordale.

Une courbe équicordale générale est l’ensemble décrit par une extrémité d’un segment de droite de longueur constante \(d\) passant par un point fixe (le point équicordal), pouvant tourner autour de ce point et glisser sur lui dans la direction de chaque extrémité, de telle sorte que l’extrémité en question arrive à la position initiale de l’autre extrémité.

Le cercle par, exemple, est une courbe équicordale. Le segment « générateur » est un diamètre et le point équicordal est le centre du cercle.

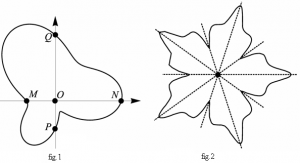
La courbe définie en coordonnées polaires par l’équation

\[\rho = 0,5 + 0,2\sin \theta + 0,2\cos 3\theta \]

est équicordale et le point \(O\) est équicordal (fig.1).

Les courbes définies en coordonnées polaires par l’équation

\[\rho = f(\theta ),\]

où \(f\) vérifie la relation

\[f(\theta ) + f(\theta + \pi ) = d,\]

sont équicordales (e.g. \(f(\theta ) = 2 + \sin \theta \)).

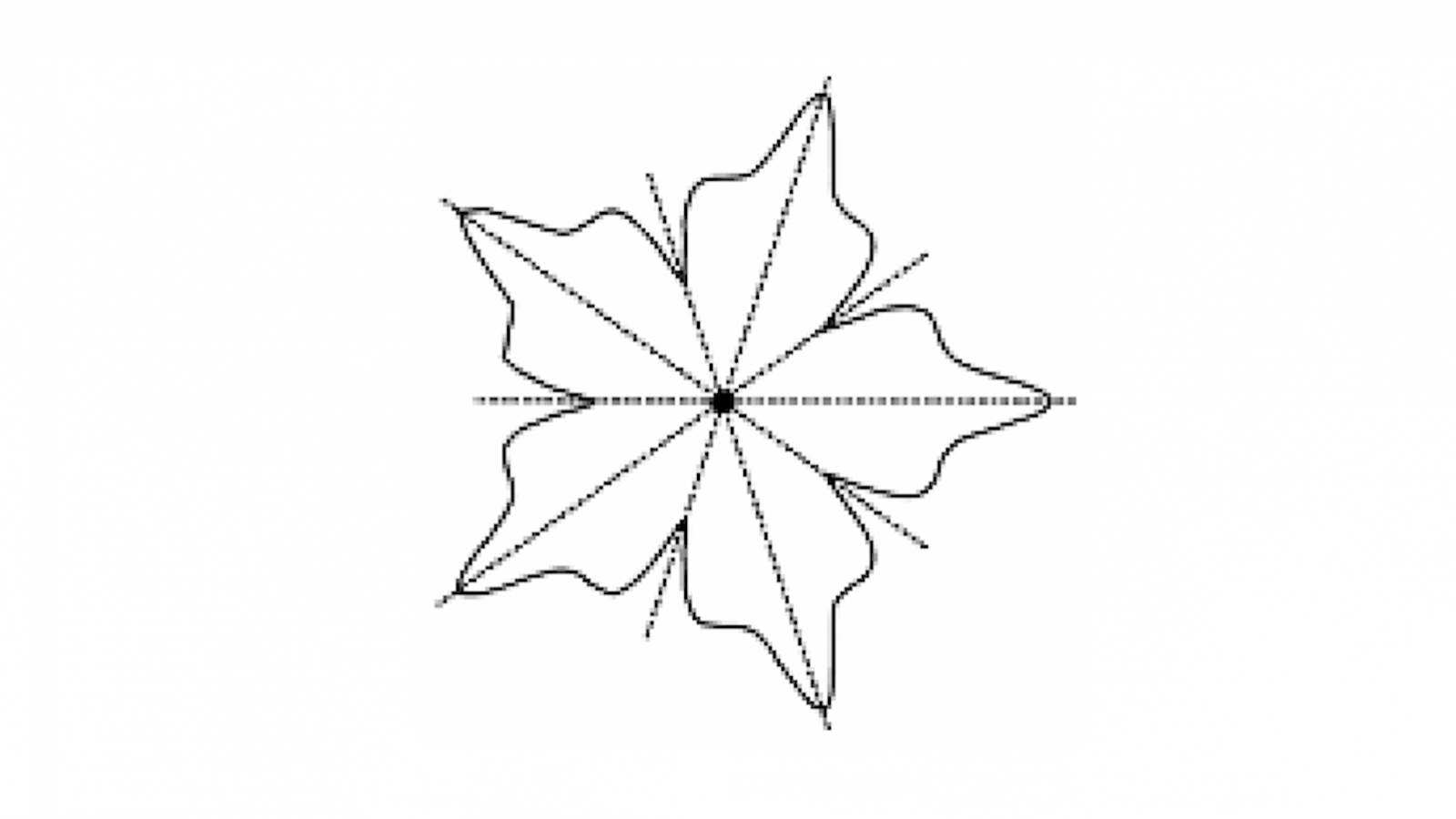
Si une courbe équicordale admet un axe de symétrie alors le point équicordal appartient à cet axe (fig.2) et le nombre de tels axes ne peut être pair.

Le problème fut posé par Fujiwara en 1916 et indépendamment par Blaschke, Rothe et Weizenböck en 1917.

En 1997 Marek R. Rychlik démontra que le problème n’a pas de solution en montrant
que le problème généralisé aux courbes {fortement étoilées} n’en a pas.

On dit qu’une partie \(E\) de \({\bf R^2}\) est étoilée par rapport au point \(O\) de \(E\) si et seulement si pour tout point \(M\) de \(E\) le segment \([OM]\) est inclus dans \(E\).
Une courbe fermée \(C\) de \({\bf R^2}\) est dite {étoilée} par rapport à \(O\) si la composante bornée de \({\bf R^2}{\rm{\backslash }}C\) est étoilée par rapport à \(O\). Une courbe \(C\) est dite {fortement étoilée} par rapport à \(O\) si toute droite contenant \(O\) rencontre \(C\) en exactement deux points.

Si \(C\) est fortement étoilée par rapport à \(O\) alors elle est étoilée par rapport à \(O\).

Si \(O\) est un point équicordal pour la courbe \(C\) alors \(C\) est fortement étoilée par rapport à \(O\).

La question originale (Fujiwara) supposait la courbe convexe, ainsi Rychlik avait résolu le problème du Point équicordal complètement.

Les courbes équicordales, comme généralisation du cercle, trouvent leurs applications par exemple en Mécanique pour la construction des pompes hydrauliques ou pneumatiques.

Références

1. Marek R. Rychlik, A complete solution to the equichordal point problem of Fujiwara, Blaschke, Rothe and Weizenböck. Inventiones. mathematicae. 129, 141–212, Springer-Verlag (1997).

2. Ferenc Adorjàn, Equichordal curves and their applications-The geometry of a pulsation-free pump, Applied Reactor Physics Department, KFKI Atomic Energy Research Institute, H-1525 Budapest, Hungary.

N.B. Ce billet est une reproduction intégrale de l’article du même nom, du manuscrit de la deuxième édition de mon livre « Le jardin des courbes. Dictionnaire raisonné des courbes planes célèbres et remarquables ».