
David Mumford est un membre éminent de l’élite mathématique des USA, avec une carrière exceptionnelle : il a d’abord été un mathématicien pur, professeur à la prestigieuse Université de Harvard, où ses travaux de géométrie algébrique lui ont valu la médaille Fields (le Prix Nobel des mathématiques) en 1974. Mais à partir des années 80 il s’est tourné vers les mathématiques appliquées, d’abord avec des travaux sur la vision par ordinateur, il s’est ensuite intéressé aux problèmes posés par les neurosciences dans leur relation avec l’intelligence artificielle. Ces trois directions de recherche ne donnent qu’une faible idée des domaines où Mumford s’est investi, car il a pratiqué en même temps une soif dévorante de connaissance qui s’est exprimée dans son blog dont il a enrichi et réuni les principaux chapitres dans ce livre Numbers and the world, Essays on math and beyond, American Mathematical Society, 2023.
La curiosité de Mumford n’a pas de limites, c’est un véritable encyclopédiste qui approfondit tous les sujets qu’il aborde de manière originale. Le résultat est un pot-pourri de thèmes qu’on peut savourer selon ses goûts – se munir parfois de quelques connaissances scientifiques.
Ainsi du rôle comparé de la beauté dans l’art et dans les mathématiques, on passe à l’avenir du projet d’intelligence artificielle générale, de la conscience des robots à la religion de Spinoza, des mathématiques de la Mésopotamie au renouvellement de la géométrie algébrique par Alexandre Grothendieck (voir aussi ici pour la traduction d’un de ses textes à ce sujet)…
Citons quelques têtes de chapitres du livre de ce grand polymathe :
Mathématiques pures
- La “règle” de Pythagore (car le “théorème” apparut d’abord sans démonstration) : sa naissance longtemps avant Pythagore, son apparition simultanée dans plusieurs cultures (Pourquoi ?) et sa diffusion ;
- La beauté des formules mathématiques se reflète-t-elle dans le cortex du mathématicien, et comment ?
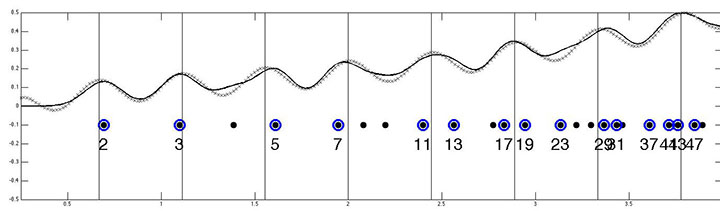
L’étude de la fonction zeta par Riemann conduit à l’idée que les logarithmes des nombres premiers présentent une certaine périodicité .
- Peut-on déceler une périodicité dans la suite des nombres premiers ?
- Comment expliquer l’oeuvre de Grothendieck à des non-spécialistes ? Un examen des difficultés de la vulgarisation.
Les mathématiques appliquées
- Les “espaces de formes” : leur théorie peut-elle prévoir les “vagues scélérates” (des vagues exceptionnelles géantes) ;
- Les intégrales de Feynmann et l’informatique quantique ;
Histoire culturelle des mathématiques de Babylone à l’Inde1Mumford est un spécialiste des anciennes mathématiques indiennes et à la Chine

Le célèbre Diagramme de Xian Tu qui a conduit à la règle de Pythagore en Chine durant la dynastie Zhou (entre 1046 et 256 av. J.C.)
L’éducation mathématique :
- Comment faire aimer par les lycéens les formules et les triangles ?
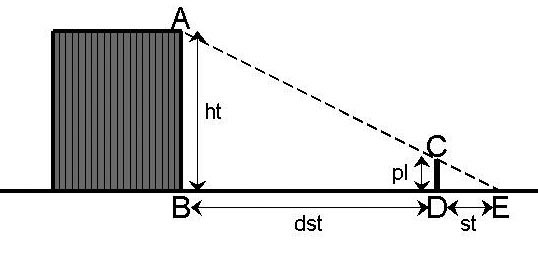
Le principe de l’évaluation de la hauteur d’un arbre

Le même principe exposé dans un livre d’un mathématicien chinois vers 260 après J.C., “le manuel de l’île de la mer”
Neurosciences : Les fonctions du cerveau et l’apprentissage profond de l’intelligence artificielle ; Les animaux ont-ils une conscience ? Peut-on imaginer des robots conscients ?

Le kéa ( sorte de perroquet de la Nouvelle Zelande ) utilise un outil et son pied pour se saisir de la nourriture .
Nous donnons une description plus précise de trois exemples de la culture encyclopédique et de l’originalité de Mumford.
Nous donnons une description plus précise de trois exemples de la culture encyclopédique et de l’originalité de Mumford.
- Le rapprochement entre la peinture et les mathématiques. Mumford pointe un rapprochement entre la naissance de l’art non-figuratif (par exemple chez Turner au XIX °s) et celle des mathématiques abstraites (qu’il illustre par le tournant représenté par Galois et Abel). Allant plus loin dans ce rapprochement entre histoire de la peinture et celle des mathématiques, il poursuit cette idée jusqu’à l’avènement de l’art moderne, avec le minimalisme de Mondrian qu’il rapproche du théorème (récent) de classification des groupes finis.
- Fonder les mathématiques appliquées. Les mathématiques reposent sur une base acceptée par les mathématiciens, celle de la théorie des ensembles et de son langage (les principes codifés par les axiomes de Zermelo-Fraenkel, ZF). Mais le tournant dans la carrière de Mumford devenu mathématicien appliqué lui a fait ressentir un manque. Comme le chapitre sur Pythagore le montre, les mathématiques ont servi, longtemps avant Euclide à modéliser les aspects quantitatifs du monde. Pourrait-on imaginer une fondation des mathématiques donnant plus de place à leur rôle de modèle ? C’est la question que s’est posée Mumford, et il donne un début de réponse qui met en jeu les probabilités (la notion de variable aléatoire) et des travaux de logique conduisant à une version affaiblie de l’axiomatique ZF.
- L’analogue de la conscience humaine existe-t-il chez les animaux et peut-elle être produite chez les robots de l’IA ?

Une pieuvre ôte le capuchon d’une jarre qui contient de la nourriture .
La question n’est qu’une étape – difficile – dans le projet encore lointain d’une intelligence artificielle générale (similaire à celle de l’homme ) ; Mumford donne des exemples (avec de belles photos) et des arguments pour nous convaincre qu’une certaine forme de conscience, avec des intensités variables, existe chez les animaux ayant un système nerveux, comme la pieuvre. Puis il décrit la question des émotions, qui lui semblent nécessaires si on veut imaginer des robots possédant une forme de conscience ; enfin il fait intervenir deux grands penseurs qui ont réfléchi – dans des directions opposées – à la question de la conscience : Einstein et Bergson, Mumford étant lui-même du côté d’Einstein. En effet la relativité met en cause notre idée du temps et de l’intuition personnelle que nous avons de l’instant , un concept mis en avant par Bergson. Cependant vers la fin de sa vie Einstein admit (dans une conversation avec le logicien Carnap) que « Bergson avait aussi des idées valables sur cette question centrale. ».
Enfin, dans une dernière partie, Mumford aborde les problèmes majeurs de nos sociétés et de l’humanité : l’explosion démographique, les débats posés par les récents progrès de la biologie (sous le titre provoquant : « Playing God with the genome »), et les espoirs qu’on peut tirer du rôle de la science. En conclusion Mumford exprime l’espoir que l’humanité conservera dans ce futur incertain
« amour, empathie, coopération »


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.