De l’irréversibilité du temps numérique

Les nombres réels n’existent pas dans l’univers fini du numérique ce qui implique d’inévitables erreurs d’arrondi. Par conséquent, qu’en est-il de la réversibilité du temps “numérique” ?

Les lois de la physique classique sont indépendantes du sens de l’écoulement du temps. Prenons un exemple simple en utilisant un mobile \(P\) de coordonnée \(X\) et de vitesse \(V\) sur une droite \(D\) et examinons son déplacement :
\[
\begin{array}{lcl}
T=0 &: &X_0 \\
T=dT &: &X_1 = X_0 + V.dT
\end{array}\]
et, à cet instant, inversons la vitesse V :\[T=2dT : X_2 = X_1 – V.dT = (X_0 + V.dT) – V.dT = X_0 \]
Ainsi, le point \(P\) est revenu à sa position de départ…

Les grandeurs \(X_i, V\) et \(dT\) sont des nombres réels ¹Rappelons que les nombres réels sont les nombres de la physique. . Évidemment, les systèmes étudiés, en physique en particulier, sont beaucoup beaucoup plus complexes que l’exemple naïf présenté ci-dessus. et en général il est nécessaire de faire appel à l’ordinateur pour les étudier. Or, malheureusement les nombres réels n’existent pas dans l’univers fini du numérique ce qui implique d’inévitables erreurs d’arrondi ! Et du coup, qu’en est-il de la réversibilité du temps “numérique” ?

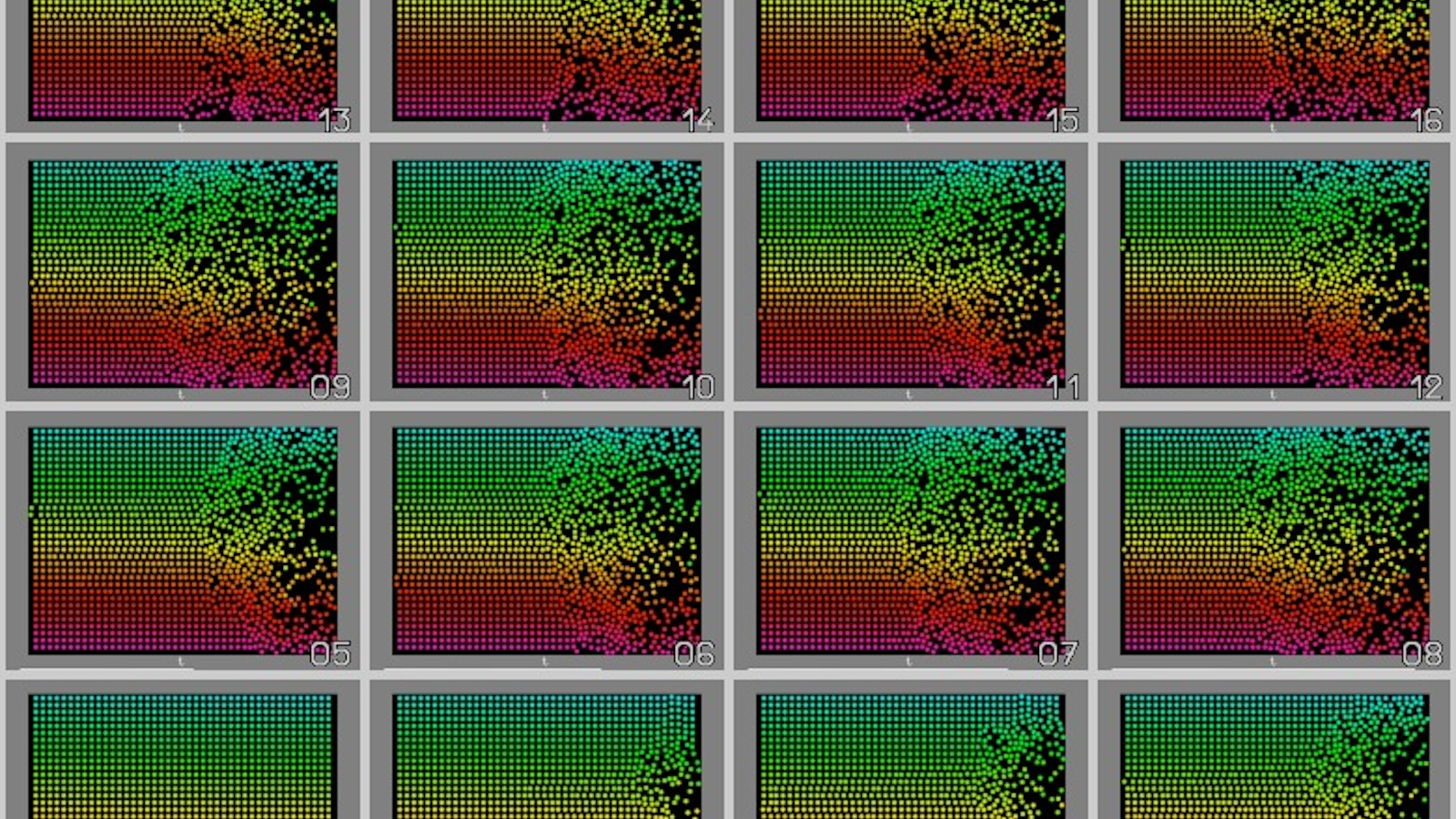
Pour répondre à cette question, prenons l’exemple du billard bidimensionnel²On trouvera dans cette galerie de nombreux exemples de billards bidimensionnels.. Utilisons donc un domaine rectangulaire plan à l’intérieur duquel nous disposons régulièrement sur un réseau carré \(N\) boules de mêmes masses et immobiles sauf une dont la vitesse est non nulle et aléatoire — au milieu à droite — ³La couleur de chaque boule est fonction de ses coordonnées initiales \({X_0,Y_0}\).. Au cours du temps, les particules se heurtent et les chocs sont parfaitement élastiques : il y a conservation de la quantité de mouvement. Au milieu temporel de cette simulation toutes les vitesses sont inversées ⁴Ce qui signifie que pour chaque vecteur vitesse \({V_x,V_y}\) est remplacé par \({-V_x,-V_y}\) au même instant. . En théorie, cela signifie que toutes les boules vont revenir à leur position de départ. Mais cela reste-t-il vrai dans un ordinateur ?

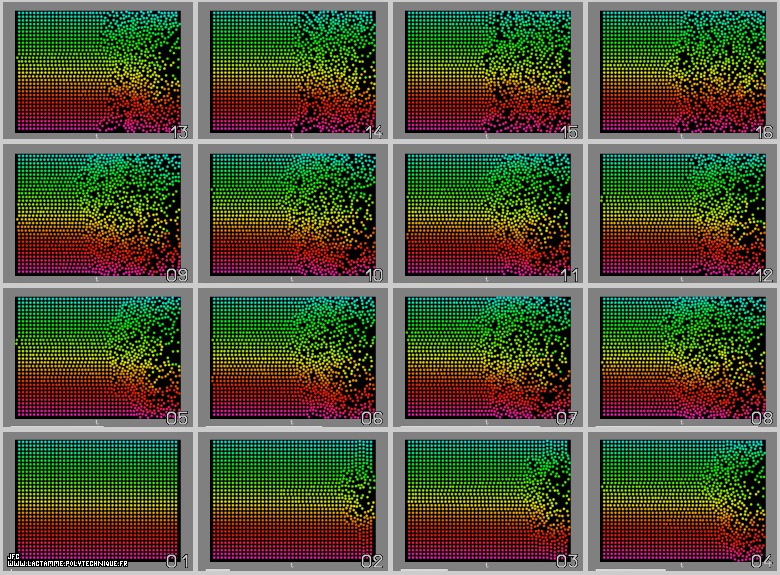
Cliquer sur les images ci-dessous pour voir les films correspondants.

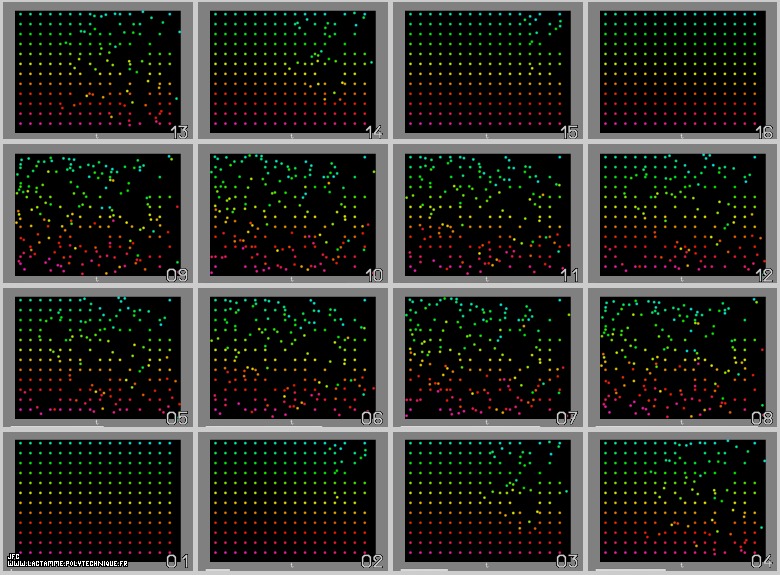
• Avec peu de particules (\(N=192\)), l’état final est identique à l’état initial. Les erreurs d’arrondi sont peu nombreuses et le processus est numériquement réversible.
  

  La réversibilité numérique du billard bidimensionnel (\(192\) particules)

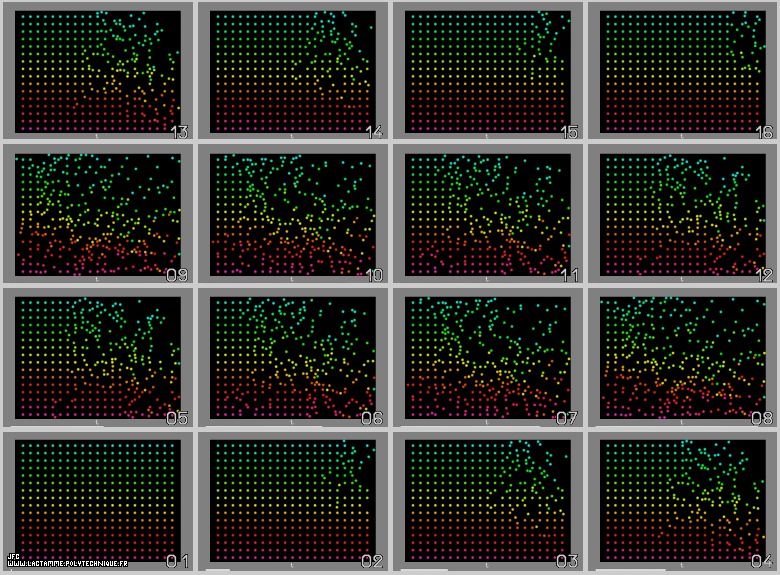
• Avec plus de particules \((N=336)\), l’état final n’est plus identique à l’état initial. Les erreurs d’arrondi sont suffisamment nombreuses pour que les particules ne reviennent pas à leur point de départ : le processus est numériquement irréversible.
  

  L’irréversibilité numérique du billard bidimensionnel (\(336\) particules)

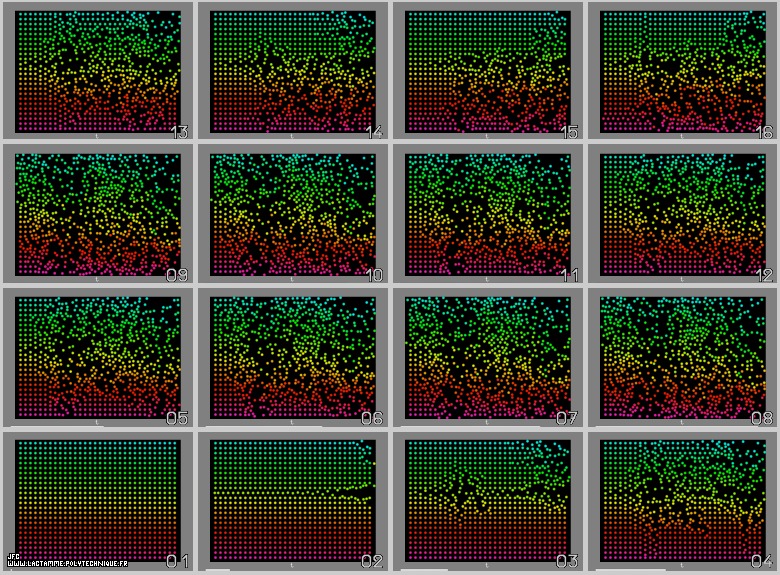
• Avec beaucoup plus de particules \((N=768)\) et \(N=1376)\), le phénomène d’irréversibilité numérique ne peut que s’aggraver !
  

  L’irréversibilité numérique du billard bidimensionnel (\(768\) particules)

  

  L’irréversibilité numérique du billard bidimensionnel (\(1376\) particules)

On observe donc une sorte d’effet de seuil : réversibilité avec peu de particules et irréversibilité lorsqu’elles sont plus nombreuses.

En conclusion et en toute généralité le temps n’est pas réversible dans nos ordinateurs, alors que la physique sous-jacente l’est…