Au delà de leurs applications, il y a des mathématiques collées à la réalité. Je voudrais commencer ici une petite promenade mathématique autour d’un concept de la vie courante. Mais mon parcours ne sera ni exhaustif, ni objectif. Au contraire, j’aimerais garder un regard subjectif.
Ce fût il y a treize ans, lors d’un colloque à Stony Brook, que cette promenade commença pour moi. Dans un très bel exposé, j’entendis parler pour la première fois d’un arbre infini imaginé par Richard Kenyon.
Un arbre infini
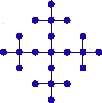
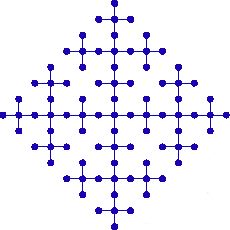
En réalité, cette figure ne montre qu’une portion finie de l’arbre infini \(K\) obtenu comme la réunion d’une suite d’arbres finis \(K_n\) dont les quatre premiers termes \(K_1\), \(K_2\), \(K_3\) et \(K_4\) sont représentés ci-dessous :
.
.
.
.
Pourquoi cet arbre est-il beau ? Voici la question à laquelle je voudrais répondre au cours de cette promenade. Je ne me souviens plus depuis quand exactement cet arbre est lié dans ma tête à une phrase de Frank Kafka
« Sie suchte etwas und er suchte etwas, » 1« Elle cherchait quelque chose et il cherchait quelque chose, ».
et une pièce de Johann Sebastian Bach 2Contrapunctus I, Die Kunst der Fugue, BWV 1080, dans une version de Chris Breemer pour Piano Society.. Mais je suis certain que, à un moment donné, peut-être même avant d’avoir compris, j’ai été amené à rechercher dans Les testaments trahis 3Milan Kundera, Les testaments trahis. Gallimard, 1993. la sensation que j’avais éprouvée lorsque j’avais lu ce livre de Milan Kundera. Je pars en quête d’une justification.
Crédits images
Álvaro Lozano Rojo
ÉCRIT PAR
Xavier Caruso
Directeur de recherche CNRS - Institut mathématique de Bordeaux
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.