
Premier défi : le problème du mois
Les rayons \([AO]\) et \([OB]\) sont perpendiculaires, \((MN)\) est parallèle à \((AB)\), \(MP=\sqrt{56}\,{\rm cm}\) et \(PN=12\,{\rm cm}\). Combien mesure le rayon du cercle ?
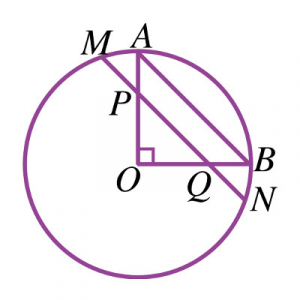
.


Solution du premier défi
Comme \(OA=OB=OM=ON\), \(O\) est sur la médiatrice de \([AB]\) et sur la médiatrice de \([MN]\). Comme ces segments sont de directions parallèles, ces deux médiatrices sont confondues. Si l’on appelle \(C\) le milieu de \([MN]\), la droite \((OC)\) est cette double médiatrice.
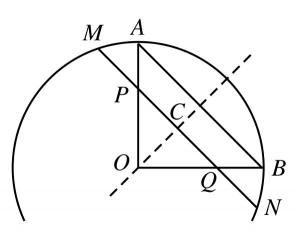
.
Le triangle \(OAB\) est symétrique par rapport à \((OC)\) et \(M\) est le symétrique de \(N\) par rapport à \((OC)\). Toute la figure est donc symétrique par rapport à \((OC)\) et \(P\) est le symétrique de \(Q\).
On en déduit que
\[12=PN=PC+CQ+QN=2PC+MP,\]
ce qui donne
\[PC=\frac{12-\sqrt{56}}2 = (6 – \sqrt{14})\,{\rm cm}.\]
On a donc
\[MC=MP+PC= \frac {12 – \sqrt{56}}2 + \sqrt{56} = \frac{12+\sqrt{56}}2 = (6 + \sqrt{14})\,{\rm cm}.\]
Par ailleurs, les angles du triangle \(OPC\) mesurent \(90^\circ\), \(45^\circ\) et \(45^\circ\) : c’est un triangle isocèle rectangle. On trouve donc que \(PC=OC\). Il reste à appliquer le théorème de Pythagore.
\begin{align*}
OM^2&=OC^2+MC^2=(6 – \sqrt{14})^2 + (6 + \sqrt{14})^2\\
&=2\times(36+14)=100.
\end{align*}
Finalement, le rayon du cercle est \(10\,\mathrm{cm}\).
Deuxième défi
Les épouses de Ben, Issa et Tao sont Léa, Aimée et Mira. Chaque couple a un fils, dont les noms sont Alex, Naël et Victor. Tao n’est ni le mari de Léa ni le père de Näel. Aimée n’est ni l’épouse d’Issa ni la mère d’Alex. Si le père d’Alex est Issa ou Tao, alors Léa est la mère de Victor. Si Léa est l’épouse d’Issa, Mira n’est pas la mère d’Alex. Trouvez les membres de chaque famille.


Solution du deuxième défi
Aimée n’est pas la mère d’Alex. Si Léa est mariée à Issa, alors Mira n’est pas nonplus la mère d’Alex, qui est donc le fils de Léa et Issa. Mais, alors, comme le père d’Alex est Issa, Léa serait aussi la mère de Victor, ce qui est impossible car elle est déjà la mère d’Alex. Par conséquent, Léa n’est pas mariée à Issa. Or, on sait déjà qu’elle n’est pas mariée à Tao, donc les couples sont Léa et Ben, Aimée et Tao et Mira et Issa.
Comme Aimée n’est pas la mère d’Alex et Tao n’est pas le père de Naël, le fils d’Aimée et Tao est Victor. Donc Alex ne peut pas être le fils d’Issa et le fils de Mira et Issa est Naël. Par élimination, celui de Léa et Ben est donc Alex.
Troisième défi
On coupe une feuille rectangulaire en quatre morceaux. Si \(A\) est un carré d’aire \(144\,{\rm cm}^2\), \(B\) un carré d’aire \(81\,{\rm cm}^2\) et \(C\) a pour aire \(102\,{\rm cm}^2\), quelle est l’aire du morceau \(D\) qui reste ?
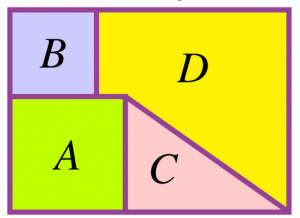
.


Solution du troisième défi
On divise la partie \(D\) comme sur la figure ci-dessous et on appelle \(x\) la longueur du segment ajouté.

.
L’aire du carré \(A\) vaut \(144\,{\rm cm}^2\), donc son côté mesure \(12\,{\rm cm}\). De même, l’aire du carré \(B\) vaut \(81\,{\rm cm}^2\), donc son côté mesure \(9\,{\rm cm}\). Le triangle \(D ‘ ‘\) est égal au triangle \(C\), donc il a la même aire, c’est-à-dire \(102\,{\rm cm}^2\). Cette aire peut aussi s’écrire \(\frac{12x}{2}\), ce qui montre que \(x=17\,{\rm cm}\). Donc le rectangle \(D ‘ \) a un côté qui mesure \(x+3=20\,{\rm cm}\) et l’autre côté qui mesure \(9\,{\rm cm}\). Son aire est donc \(180\,{\rm cm}^2\). Au total, l’aire du morceau \(D=D ‘ +D ‘ ‘\) est \(180+102=282\,{\rm cm}^2\).
Quatrième défi
Quelle est la somme des chiffres du produit
\(999\, 999 \times 666 \, 666\) ?


Solution du quatrième défi
Remarquons que \(9 \times 6=54\) dont la somme des chiffres est \(m_1=5+4=9=1 \times 9\).
En continuant,
\[99 \times 66=66(100-1)=6600-66=6534,\]
dont la somme des chiffres est \(m_2=6+5+3+4=18=2 \times 9\).
De même, on a \(999 \times 666=665\,334\),
dont la somme des chiffres est \(m_3=6+6+5+3+3+4=27=3 \times 9\).
De manière analogue,
\begin{eqnarray*}
999\,999\times 666\,666 & = & 666\,666\times(10^6-1)\\
& = & 666\,666\,000\,000 \,-\, 666\,666\\
& = & 666\,665\,333\,334,
\end{eqnarray*}
dont la somme des chiffres est
\[(6\times 5)+5+(3\times 5)+4=30+5+15+4=54.\]
Cinquième défi
Entre 1 et 2024, ces deux nombres inclus, combien d’entiers peuvent s’écrire comme la différence de deux carrés d’entiers ?


Solution du cinquième défi
Réponse : il existe \(1012+506=1518\) nombres entiers entre \(1\) et \(2024\) qui peuvent s’écrire comme la différence de deux carrés.
On veut trouver tous les entiers \(n\), avec \(1\leq n\leq 2024\), tels que \(n=x^2-y^2=(x+y)(x-y)\), avec \(x\geq 0\) et \(y\geq 0\) des nombres entiers.
Si \(n\) est impair, posons \(n=2k+1\) et alors \(n=(k+1)^2-k^2\).
Si \(n\) est pair, comme \(n=(x+y)(x-y)\), au moins un des deux facteurs (\(x+y\) ou \(x-y\)) doit être pair.
Mais comme \(x+y+(x-y)=2x\) est pair, les deux nombres \(x+y\) et \(x-y\) doivent être pairs.
Par conséquent, \(n=(x+y)(x-y)\) doit être un multiple de \(4\).
Une possibilité pour l’écrire comme une différence de deux carrés est de poser \(x-y=2\) et \(x+y=2(\frac{n}{4})\). En résolvant ce système, on trouve \(x=1+\frac{n}{4}\) et \(y=\frac{n}{4}-1\), ce qui donne \(n=(1+\frac{n}{4})^2-(\frac{n}{4}-1)^2\).
Comme il y a \(1012\) entiers impairs et \(\frac{2024}{4}=506\) entiers multiples de \(4\) entre \(1\) et \(2024\), il existe \(1012+506=1518\) nombres entiers entre \(1\) et \(2024\) qui peuvent s’écrire comme la différence de deux carrés.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


14h46
1er défi
Le triangle \(POQ\) est isocèle et rectangle en \(O\) donc le théorème de Pythagore donne \(PQ^2 = OP^2 + OQ^2 = 2 OP^2\), d’où \(OP^2 = \frac{PQ^2}{2}\) et \(OP = \frac{PQ}{\sqrt{2}} = – \frac{PQ}{cos(\frac{3\pi}{4})} \). De plus l’angle en \(P\) est \( \frac{\pi}{4}\), donc dans le triangle \(OPM\), l’angle en \(P\) est \( \frac{3\pi}{4}\). Pour \(OPM\) la loi des cosinus s’écrit alors \(OM^2 = OP^2 + PM^2-2OP.PM.cos(\frac{3\pi}{4}) = \frac{PQ^2}{2} + PM^2 +2PQ.PM \).
Or \(PQ = PN – QN = PN – PM\) puisque \(PM = QN\). Donc : \(OM^2 = \frac{(PN – PM)^2}{2} + PM^2 +2(PN – PM)PM = \frac{PN^2 + PN.PM – PM^2}{2}\) \(OM^2 = \frac{12^2 + 24 \sqrt{56} – 56}{2}\) \(OM = 2\sqrt{11 + 6\sqrt{14}} = 11,6 \) environ.
10h42
Petite coquille à la ligne 4 : \(cos({3 \pi \over 4}) = -{\sqrt2 \over 2}\) D’où un facteur 2 erroné à la ligne 8. On obtient avec votre méthode : \(OM^2 = {{PN^2 + PM^2} \over 2} \) Ce qui permet bien de retrouver le résultat de François.
18h28
1er défi
\(OP= \frac {PQ} {\sqrt{2}} = \frac {12-\sqrt{56}} {\sqrt{2}} \widehat{\vec{OP}\vec{PM}}=\frac {\Pi} {4} R^2=OP^2+PM^2+2OP*PM*\cos(\frac {\Pi} {4}) =100\) D’où \(R = 10\)
10h33
3e défi
Si l’aire du carré A vaut 144 alors son côté vaut 12. De même l’aire de B étant 81 son côté vaut 9. Donc le petit côté du rectangle vaut 9+12, soit 21. Le triangle C à pour côté celui de A, soit 12, son aire étant 102, alors son grand côté est (2×102):12, soit 17. Donc le grand côté du rectangle vaut 12+17, soit 29. Et l’aire de D est celle du grand rectangle, soit 21×29, diminuée de celle de A, B et C, soit 609-(144+81+102), Donc 282 cm2
14h36
2e défi
Nommons les différentes assertions : A1 : Tao n’est ni le mari de Léa ni le père de Naël. A2 : Aimée n’est ni l’épouse d’Issa ni la mère d’Alex. P1 : Si le père d’Alex est Issa ou Tao, alors Léa est la mère de Victor. P2 : Si Léa est l’épouse d’Issa, Mira n’est pas la mère d’Alex.
Raisonnons.
Si Léa est l’épouse d’Issa, d’après P2, Mira n’est pas la mère d’Alex, et d’après A2, Aimée n’est pas la mère d’Alex, donc la mère d’Alex est Léa. Mais alors par contraposition de P1, Ben est le père d’Alex. Ce qui est absurde puisque le père d’Alex devrait être le mari de sa mère Léa : Issa. Par conséquent, Léa n’est pas l’épouse d’Issa. De plus, d’après A1, Léa n’est pas l’épouse de Tao. Nous obtenons alors une première certitude : LEA EST L’EPOUSE DE BEN. Il en découle d’après A2 que : AIMEE EST L’EPOUSE DE TAO. Et par suite : MIRA EST L’EPOUSE DE ISSA. Nous avons les trois couples.
Cherchons maintenant le père d’Alex. Si le père d’Alex est Issa ou Tao. D’après A2, Aimée n’est pas la mère d’Alex. Et donc Tao, le mari d’Aimée, ne peut être le père d’Alex. Le père d’Alex est donc Issa, et la femme d’Issa, Mira est sa mère. D’après P1, Léa est la mère de Victor, et donc Aimée est la mère de Naël. Ce qui est absurde, car le mari d’Aimée est Tao, qui d’après A1 n’est pas le père de Naël. On en déduit que le père d’Alex n’est ni Issa ni Tao. Donc c’est Ben, et sa mère est Léa. D’après A1, Naël n’est pas le fils de Tao, donc il est le fils de Issa et Mira. Par suite, Victor est le fils de Tao est Aimée.
Nous avons donc les trois familles : Léa, Ben et Alex Aimée, Tao et Victor Mira, Issa est Naël
13h49
4e défi
\(999 999\times 666 666=(1 000 000 – 1)\times 666 666 = 666 666 000 000 – 666 666 = 666 665 333 334 $. La somme des chiffres est $5 \times (6+3) + 5+4=6\times9=54\)
19h01
5e défi
\(2025=45^2-1^2\)
Je peux ensuite soustraire \(2^2\) puis \(3^2\) etc. Donc pour \(45^2\), je peux soustraire de \(1^2\) à \(44^2\) soient \(44\) nombres.
19h16
Pour \(44^2\), je peux commencer par soustraire \(0^2\) puis soustraire jusqu’à \(43^2\). Je vais donc aussi soustraire \(44\) nombres à \(44^2\). Pour \(43^2\), je vais donc pouvoir soustraire \(43\) nombres et ainsi de suite jusqu’à \(1^2\) auquel je soustrais un seul nombre, \(0^2\). Le total des nombres soustraits à tous les carrés possibles est donc \(44+45*44/2=1034\). Le nombre maximal d’entiers qui peuvent s’écrire comme la différence de deux carrés d’entiers est donc \(1034\). Je ne sais actuellement pas trouver le nombre exact car je ne sais pas compter le nombre de doublets, triplets, etc. En effet, par exemple, \(24=5^2-1^2=7^2-5^2\)
19h20
Ouh la la complètement faux car par exemple \(47^2-14^2=2013\)
23h36
Soit N entre 1 et 2024. Si N est congru à 0 modulo 4 il s’écrit \( N = 4n = 2(2n) = ((n+1)-(n-1))((n+1)+(n-1)) = (n+1)^2-(n-1)^2 \). Si N est congru à 1 ou 3 modulo 4 il est impair et s’écrit \( N = 2n + 1 = ((n+1)-n)((n+1)+n) = (n+1)^2-n^2 \). Par contre si N est congru à 2 modulo 4 il ne peut pas être une différence de 2 carrés. En effet \( 0^2 = 4*0 + 0\), \( 1^2 = 4*0 + 1\), \( 2^2 = 4*1 + 0\), \( 3^2 = 4*2 + 1\) donc tout carré est congru à 0 ou 1 modulo 4, et donc toute différence de carrés est congrue à 0, 1 ou -1, soit 3. Ainsi, sur 4 nombres consécutifs il y en a toujours exactement 3 qui s’écrivent comme différence de 2 carrés. Comme \( 2024 = 4*506 \), il y en a \( 3*506 = 1518 \) entre 1 et 2024.
16h09
On remarque d’abord – que tous les nombres impairs ≤2024 conviennent, En effet si 2n+1=a²-b² alors 2n+1=(a-b)(a+b) Et 2n+1=(2n+1)(1) Donc (2n+1)(1)=(a+b)(a-b) 2n+1=a+b et 1=a-b D’où a=n+1 et b=n On a donc déjà 2024/2=1012 possibilités – pour les nombres pairs, seuls une partie d’entre eux conviennent. En effet: Si 2n= a²-b²=(a+b)(a-b) 2n=(2n)(1)=(a+b)(a-b) Donc 2n=a+b et 1=a-b D’où a=(2n+1)/2 et b=(2n-1)/2 Ces 2 nombres sont entiers si n= 2p et donc si le nombre pair initial (2n) est un multiple de 4 (2n=4p) Donc parmi les nombres pairs seuls les multiples de 4 conviennent. On a donc 2024/4=506 possibilités Soit au total 1012+506= 1518 possilités Il convient également d’ajouter ces mêmes nombres mais négatifs puisque (-a)²-(-b)²=a²-b² Soit au total 2×1518= 3036 possibilités
8h42
1 Oups! 2 erreurs à corriger 1) concernant les nombres paires. Au lieu de (2nx1) =(a-b)(a+b) il faut prendre 2n= (a-b)(a+b) D’où n=a+b et 2=a-b On tire a=(n+2)/2 et b=(n-2)/2 Pour que a et b soient entiers il faut n paire et donc 2n multiple de 4. 2) le nombre total est bien de 1012+506=1518 (et non pas 3036 !)