
Premier défi
Combien peut-on former de triangles rectangles dont les longueurs des côtés de l’angle droit sont entières et dont la longueur de l’hypoténuse est \(\sqrt{2023}\)?


Solution du premier défi
Réponse : aucun.
Supposons qu’au moins un tel triangle rectangle existe et notons \(x\) et \(y\) les longueurs des deux côtés de l’hypoténuse.
Le théorème de Pythagore assure que l’on a l’égalité \(x^2+ y^2 = 2023\).
Les deux nombres \(x\) et \(y\) ne peuvent donc être simultanément pairs ou simultanément impairs (sinon, leurs carrés garderaient leur parité et dans tous les cas, la somme deviendrait paire, ce que n’est pas 2023).
Posons, sans perte de généralité, \(x=2n\) et \(y=2m+1\) (avec \(n\) et \(m\) entiers). On a alors
\[
\begin{eqnarray*}
4n^2+(2m+1)^2 &=& 2023\\
4n^2 + 4m^2 + 4m +1 &=& 2023\\
4n^2+4m^2+4m &=& 2022\\
n^2+m^2+m&=& 505{,}5.
\end{eqnarray*}
\]
La dernière égalité est impossible car \(n\) et \(m\) sont entiers !
Il n’existe donc aucun triangle rectangle dont les longueurs des côtés de l’angle droit sont entières et dont l’hypoténuse mesure \(\sqrt{2023}\).
Deuxième défi
Claire, Marie, Louis, Peter et Julien vont au cinéma et s’installent sur cinq fauteuils consécutifs. Peter n’a pas de femme à sa gauche ; Marie est assise entre deux hommes ; Julien est entre deux femmes ; Claire et Louis ont chacun un homme à leur gauche. Comment sont-ils installés ?


Solution du deuxième défi
Réponse : Peter, Louis, Marie, Julien et Claire
Comme Marie est assise entre deux hommes, Julien ne peut être qu’à sa droite car Peter n’a pas de femme à sa gauche et Louis a un homme à sa gauche.
De plus, comme Julien est entre deux femmes, Claire doit être à sa droite.
Enfin, à la gauche de Marie, il ne peut y avoir que Louis, puisque lui doit avoir un homme à sa gauche.
Par conséquent, l’ordre est le suivant (de gauche à droite du point de vue des amis) :
Peter, Louis, Marie, Julien et Claire.
Troisième défi
Quelle est l’aire de la région coloriée ?
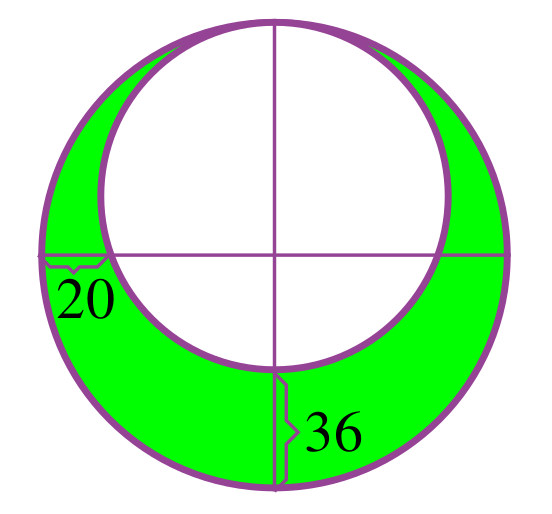


Solution du troisième défi
Réponse : \(3276\pi\)
Notons \(x\) le rayon du petit cercle et \(y\) le rayon du grand cercle.
Considérons le triangle rectangle représenté ci-dessous dont un des sommets est le centre du petit cercle.
Ses côtés de l’angle droit ont donc pour longueurs \(y-x\) et \(y-20\) et son hypoténuse a pour longueur \(x\).
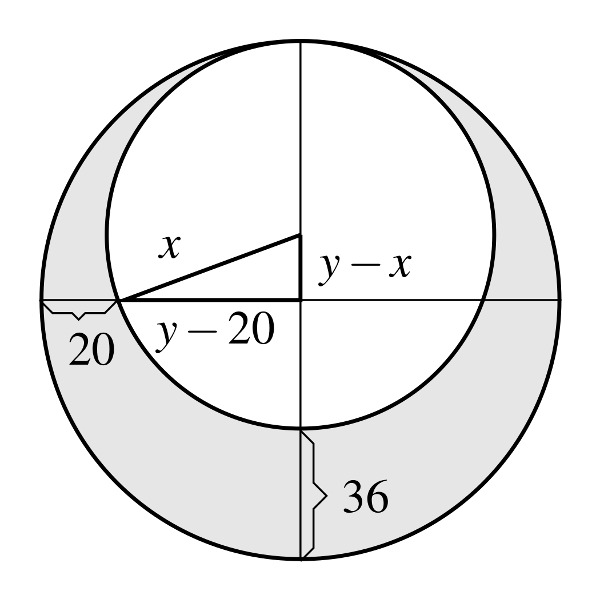
En utilisant le théorème de Pythagore, on obtient~:
\[
\begin{eqnarray*}
(y-x)^2+(y-20)^2 &=& x^2\\
y^2-2xy+x^2+y^2-40y+400 &=& x^2\\
y^2-xy-20y+200 &=& 0.
\end{eqnarray*}
\]
D’un autre côté, on a l’égalité \(2y = 36+2x\), donc \(x=y-18\).
En substituant dans la relation précédente, on obtient successivement~:
\[
\begin{eqnarray*}
y^2-(y-18)y-20y+200 &=& 0\\
y^2-y^2+18y-20y+200 &=&0\\
-2y + 200 &=&0\\
y &=& 100.
\end{eqnarray*}
\]
Il en découle que \(x=82\).
Par suite, l’aire du petit disque est \(82^2\pi\) et l’aire du grand disque est \(100^2\pi\).
Finalement, l’aire de la région colorée est \((100^2-82^2)\pi=3276\pi\).
Quatrième défi
Combien de litres de lait à \(4\,\%\) de matière grasse doit-on ajouter à du lait à \(1\,\%\) de matière grasse pour obtenir \(12\) litres de lait à \(2\,\%\) de matière grasse ?


Solution du quatrième défi
Réponse : \(4\) litres de lait à \(4\,\%\) avec \(8\) litres de lait à \(1\,\%\).
Si \(1\) litre de lait contient \(4\,\%\) de matière grasse, il contient \(0{,}04\) litre de matière grasse.
De manière similaire, \(1\) litre de lait à \(1\,\%\) de matière grasse contient \(0{,}01\) litre de matière grasse.
On doit former \(12\) litres de lait dont \(0{,}24\) litres de matière grasse pour obtenir \(12\) litre de lait à \(2\,\%\) de matière grasse.
Ainsi, si \(n\) est le nombre de litres à \(4\,\%\) et \(m\) le nombre de litres à \(1\,\%\), on doit avoir :
\[
\left\{
\begin{array}{rcl}
n+m &=& 12 \\
0{,}04n+0{,}01m &=& 0{,}24.
\end{array}
\right.
\]
En multipliant par \(100\) la seconde équation et en soustrayant la première, on obtient \(n = 4\), donc \(m=8\).
On doit donc mélanger \(4\) litres de lait à \(4\,\%\) de matière grasse avec \(8\) litres de lait à \(1\,\%\) de matière grasse pour obtenir \(12\) litres de lait à \(2\,\%\) de matière grasse.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


10h02
1er défi
On cherche \(a\) et \(b\) entiers tels que \(a^2 + b^2 = 2023\).
Comme tout carré est congru à \(0\) ou \(1\) modulo \(4\) (\(0^2 \equiv 2^2 \equiv 0 [4]\) et \(1^2 \equiv 3^2 \equiv 1 [4]\)), une somme de carrés est congrue à \(0\), \(1\) ou \(2\) modulo \(4\).
Il n’existe donc aucune décomposition en somme de carrés pour \(2023 = 4 \times 505 + 3\), et plus généralement il n’y en a pas pour tout nombre congru à \(3\) modulo \(4\).
10h37
1er défi
Il faudrait donc trouver \(a\) et \(b\) entiers tels que \(a^2 + b^2 = 2023\).
Un petit code qui génère des entiers a entre 1 et \([ \sqrt{2023} ]\) ne trouve aucune paire.
Je reste curieuse d’une solution élégante sur la non-existance de \((a,b)\).
19h38
1er défi
Nous cherchons 2 naturels a et b tels que a^2+b^2=2023.
a et b n’ont pas la même parité car 2023 est impair.
Supposons a pair et b impair d’où il existe deux naturels k et l tels que a=2k et b= 2l+1.
En remplaçant a et b par ces valeurs nous obtenons : 4k^2+4l^2+4l+1=2023
D’où 4 divise 2022 ce qui n’est pas possible.
Donc il n’existe pas de naturels a et b.
7h44
2e défi
Bonjour
Julien étant entre deux femmes, il n’est pas à gauche.
Marie étant entre deux hommes , elle n’est pas à gauche.
Claire et Louis ayant un homme à leur gauche, ils ne sont pas à gauche, donc
seul Peter peut être à gauche.
Louis ayant à sa gauche un homme, cet homme est Peter car Julien est entre deux femmes , donc Peter est à gauche et Louis à sa droite.
Marie étant entre deux hommes ne peut être qu’entre Louis et Julien.
De la gauche vers la droite, l’ordre est
Peter, Louis, Marie, Julien, Claire.
9h17
Pareil après un tâtonnement 🙂
8h17
3e défi
Soit \(R\) le rayon du grand cercle et \(r\) celui du petit, on a \(R = r +18\). Dans le repère orthonormé centré au centre du grand cercle les coordonnées du centre du petit cercle sont \((0,18)\). L’équation du petit cercle est donc \(X^2 +(Y-18)^2=(R-18)^2\). Son intersection avec l’axe des \(X\) est \(\pm(R-20)\).
Donc \((R-20)^2+18^2=(R-18)^2\) et \(R=100\), \(r=82\). L’aire colorée vaut donc \( \pi(R^2-r^2) = 3276\pi \sim10292\).
12h56
François
voir la figure
16h28
ROUX
Même valeur mais sans calculer les rayons 😀
7h53
4e défi
La quantité de matière grasse est :
\(\dfrac{4x}{100}\) dans \(x\) litres de lait à \(4\)%
\(\dfrac{12-x}{100}\) dans \(12-x\) litres de lait à \(1\)%
\(\dfrac{2 \times 12}{100}\) dans \(12\) litres de lait à \(2\)%
Donc :
\(\dfrac{4x}{100} + \dfrac{12-x}{100} = \dfrac{2 \times 12}{100}\)
\(4x + 12 – x = 24\)
\(3x=12\)
\(x=4\)
14h24
4e défi
Méthode arithmétique.
On part de 12l à 1%.
si on remplace 1l à 1% par 1l à 4% l’ensemble augmente de 3/12 = 0,25%
Puisqu’on veut passer de 1 à 2 il faudra répéter 4 fois l’opération.
22h11
4e défi
0,04y+0,01(12-y)=0,02×12
> y=4