Défis de avril 2023

Écrit par Romain Joly

Publié le 30 avril 2023

Premier défi

Simon et Noémie démarrent sur une piste circulaire en des points diamétralement opposés. Ils se mettent à courir à vitesse constante dans des sens opposées. Ils se rencontrent une première fois alors que Simon a couru $100 m$ , puis une seconde fois alors que Noémie a couru $150 m$ depuis la première fois qu’ils s’étaient rencontrés. Quelle est la longueur de la piste ?

Solution du premier défi

Réponse : la longueur de la piste est 350 mètres.

Notons $L$ la longueur de la piste. Lorsqu’ils se rencontrent pour la première fois, ils ont parcouru, à eux deux, la moitié de la longueur de la piste.

Donc, comme Simon a couru $100 m$ , Noémie a couru $\frac{L}{2} - 100$ mètres.

Entre la première et la seconde fois qu’ils se rencontrent, ils courent à eux deux $L$ mètres.

Mais comme ils courent à vitesse constante, Noémie a donc nécessairement couru le double de la distance qu’elle avait courue avant la première fois qu’ils se sont croisés.

Ainsi, on a $2 (\frac{L}{2} - 100) = 150$ et donc $L = 350 m$

Deuxième défi

Cinq pirates se partagent le contenu d’un coffre au trésor. Abel prend un huitième du total. Ensuite, Betti prend un sixième de ce qui reste, puis Clélia un septième du reste, puis Daniel un cinquième du reste, puis Éloïse un quart du reste et ils conviennent d’enterrer l’argent restant. Quels sont les pirates qui ont reçu la même somme d’argent ?

Solution du deuxième défi

La réponse est : Abel, Daniel et Éloïse ont la même somme d’argent.

Soit $S$ la somme d’argent dans le coffre.
Abel prend $\frac{S}{8}$ et il reste donc $\frac{7 S}{8}$ . On obtient successivement les actions suivantes~:

– ~Betti prend $\frac{1}{6} \times \frac{7 S}{8}$ et il reste $\frac{5}{6} \times \frac{7 S}{8} .$

-~Puis Clélia prend $\frac{1}{7} \times \frac{5}{6} \times \frac{7 S}{8} = \frac{5 S}{48}$ et il reste $\frac{6}{7} \times \frac{5}{6} \times \frac{7 S}{8} = \frac{5 S}{8} .$

-~Ensuite, Daniel prend $\frac{1}{5} \times \frac{5 S}{8} = \frac{S}{8}$ et il reste $\frac{4}{5} \times \frac{5 S}{8} = \frac{S}{2} .$

-~Enfin, Éloïse prend $\frac{1}{4} \times \frac{S}{2} = \frac{S}{8} .$

Abel, Daniel et Éloïse ont donc la même somme d’argent.

Troisième défi

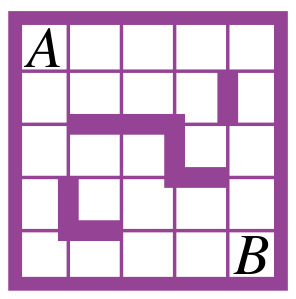
Combien y a-t-il de chemins entre les points $A$ et $B$ si l’on se déplace de case en case, seulement de gauche à droite, de haut en bas et sans traverser les murs surlignés ?

Solution du troisième défi

Réponse : il y a 12 façons d’aboutir au point B en ne traversant aucun mur.

Écrivons dans chaque carré le nombre de façons de le relier à $A$ .

Tous les carrés de la première ligne contiennent un $1$ , puisqu’il n’y a qu’une seule façon d’y accéder depuis $A$ ~: en se déplaçant vers la droite.

De même, le premier carré de la seconde ligne contient un $1$ , mais le second carré de la seconde ligne contient un $2$ , car il y a deux façons d’y accéder depuis $A$ : en arrivant soit par le haut, soit par la gauche.

Les carrés suivants de la deuxième ligne contiennent un $3$ , un $4$ et enfin un $1$ , puisque le dernier carré de la deuxième ligne n’est accessible que par le haut.

Quatrième défi

La suite $2$ , $3$ , $5$ , $6$ , $7$ , $10$ , $11$ , $\dots$ contient tous les nombres entiers positifs qui ne sont ni des carrés parfaits ni des cubes parfaits. Déterminer le $500^{e}$ entier de cette suite.

Solution du quatrième défi

La réponse est : $528$ .

Entre $1$ et $500$ , il y a $⌊ \sqrt{500} ⌋ = 22$ carrés parfaits et $⌊ \sqrt[3]{500} ⌋$ $= 7$ cubes parfaits (où $⌊ x ⌋$ désigne la partie entière de $x$ ).

Cependant, certains de ces entiers sont à la fois des carrés et des cubes : il s’agit de $1$ et de $64 = 2^{6} = 8^{2} = 4^{3}$ (le suivant, $3^{6} = 729$ , est plus grand que $500$ ).

Parmi les entiers entre $1$ et $500$ , il y en a donc $22 + 7 - 2 = 27$ qui sont des carrés ou des cubes et qui sont donc exclus de notre suite.

On doit donc encore chercher $27$ entiers de la suite supérieurs à $501$ .

Entre $501$ et $527$ , il n’y a pas de carrés parfaits à enlever mais il y a un cube parfait, $8^{3} = 512$ .

On en déduit que le nombre cherché est $528$ .

Post-scriptum

Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.

Crédits images

©JROBALLO / Adobestock

Commentaires

Al_louarn

avril 7, 2023
9h06

1er défi

Soient $s (t)$ et $n (t)$ les distances parcourues respectivement par Simon et Noémie en un temps $t$ , et $x$ la longueur de la piste.
Pendant la durée $t_{1}$ entre le départ et la première rencontre, Simon parcourt $s (t_{1}) = 100$ m et Noémie parcourt $n (t_{1}) = x / 2 - 100$ m.
Pendant la durée $t_{2}$ entre les deux premières rencontres, Simon parcourt $s (t_{2}) = x - 150$ m et Noémie parcourt $n (t_{2}) = 150$ m.
Comme les vitesses $\frac{s (t)}{t}$ et $\frac{n (t)}{t}$ sont constantes, le rapport $\frac{s (t)}{n (t)}$ est lui aussi constant donc :
$\frac{x - 150}{150} = \frac{100}{x / 2 - 100} = \frac{200}{x - 200}$
$(x - 150) (x - 200) = 200 \times 150$
$x^{2} - 350 x = 0$
$x = 350$

Kamakor

avril 8, 2023
3h42

1er défi

Puisque Simon et Noémie courent à vitesse constante, la distance qu’ils parcourent (ajoutée ou séparément) est proportionnelle au temps. Ils mettent donc, à deux, deux fois plus de temps pour parcourir la longueur de la piste après leur première rencontre que pour en parcourir la moitié avant. Avec deux fois plus de temps, Simon a ainsi parcouru $2 \times 100 = 200$ m en deuxième période. La longueur de la piste est donc $200 + 150 = 350$ m

Al_louarn

avril 12, 2023
11h00

Très élégant !

Connectez-vous pour répondre

Philippe Gay

avril 14, 2023
11h11

2e défi

Abel : 12.5%
Betti : 14.6%
Clélia : 10.4%
Daniel : 12.5%
Éloïse : 12.5%
Reste : 37.5%.

Donc : Abel, Daniel et Éloïse.

ROUX

avril 14, 2023
13h16

Bonjour,
comment avez-vous fait ?
Cordialement,

Connectez-vous pour répondre

Philippe Gay

avril 14, 2023
16h02

Bonjour,
Cela ressemble à ce que propose Poss Jean-Louis ci-dessous, mais sous forme de tableau, peu pratique à transcrire.
Cordialement.

Poss Jean-Louis

avril 14, 2023
11h44

2e défi

Soit s le contenu du coffre.

— Abel reçoit a = s/8.
— Betti reçoit b=1/6(s−a)=7s/48.
— Clélia reçoit c=1/7(s−a−b)=5s/48.
— Daniel reçoit d=1/5(s−a−b−c)=s/8.
— Éloïse reçoit e=1/4(s−a−b−c−d)=s/8.

Abel, Daniel et Éloïse reçoivent la même somme d’argent.

Remarque : les pirates se sont partagé a + b + c + d + e = 5s /8.

Celem Mene

avril 14, 2023
11h53

2e défi

Comme la somme totale doit être divisée successivement par 8, 6, 7, 5 et 4, on va créer un nombre arbitraire à l’aide de ces facteurs, calculer la part de chacun, la soustraire du total, et voir à la fin celles qui sont identiques.

Soit : 8 * 6 * 7 * 5 * 4 = 6’720

Part d’Abel : 6’720 / 8 = 840, reste : 6’720 – 840 = 5’880,
Part de Betti : 5’880 / 6 = 980, reste : 5’880 – 980 = 4’900,
Part de Clélia : 4’900 / 7 = 700, reste : 4’900 – 700 = 4’200,
Part de Daniel : 4’200 / 5 = 840, reste : 4’200 – 840 = 3’360,
Part d’Éloïse : 3’360 / 4 = 840, reste : 3’360 – 840 = 2’520.

Il ressort que les parts d’Abel, Daniel et Éloïse sont identiques.

ROUX

avril 14, 2023
18h55

Vous pouvez joindre des images : une copie d’écran ?
Les réponses sans les démarches, ici, ça ne m’intéresse pas (dans des QCM d’examens ou de concours, ok, pourquoi pas, mais ici, non).

Al_louarn

avril 15, 2023
9h32

2e défi

Si dans un reste $r$ un pirate prend une part $P = \frac{r}{k}$ , alors $r = k P$ et il laisse après lui un nouveau reste $r - P = (k - 1) P$ .
Ainsi :
$B = \frac{8 - 1}{6} A = \frac{7}{6} A$
$C = \frac{6 - 1}{7} B = \frac{5}{7} \frac{7}{6} A = \frac{5}{6} A$
$D = \frac{7 - 1}{5} C = \frac{6}{5} \frac{5}{6} A = A$
$E = \frac{5 - 1}{4} D = D = A$

Philippe Gay

avril 15, 2023
10h33

2e défi

Voici une capture d’écran, sur le calcul purement numérique ;Après je vous laisse compléter la partie algébrique.

ROUX

avril 15, 2023
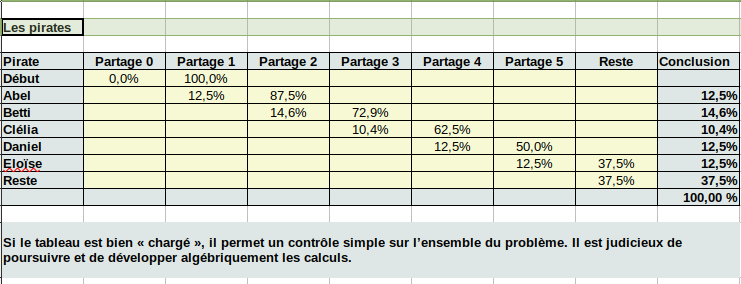
16h26

2e défi

Au moins dix caractères

Philippe Gay

avril 15, 2023
18h38

Oui, c’est bien là l’idée.

Connectez-vous pour répondre

Blaxapate

avril 19, 2023
18h45

2e défi

Si un·e pirate prend 1/n du trésor, alors le reste du trésor est (n-1)/n. Si un·e deuxième pirate prend 1/m de ce qu’il reste, alors le reste est (n-1)(m-1)/nm. Le même que si l’on avait d’abord pris 1/m et ensuite 1/n ! Chacune des parts dépend de l’ordre dans lequel elles sont prises, mais le reste du trésor n’en dépend pas.

Deuxième observation, si un·e pirate prend 1/n du trésor, puis un·e deuxième en prend 1/(n-1), les deux pirates reçoivent la même somme.

Donc, si Cléia et Betti avaient échangé leur place, tout le monde aurait reçu la même somme ! En passant avant Cléia, Betti obtient une somme plus grande, Cléia une plus petite, mais les autres pirates ne sont pas impacté·e·s, et donc leurs parts sont identiques.

Al_louarn

avril 21, 2023
10h38

3e défi

Si on écrit dans chaque case $X$ le nombre de chemins qui mènent à la case $B$ , alors $X$ doit contenir la somme de la case située à droite de $X$ si le côté droit de $X$ n’est pas un mur $+$ la case située en bas de $X$ si le côté bas de $X$ n’est pas un mur.

En partant de la case $B$ où l’on écrit $1$ , on peut alors remplir le tableau diagonale par diagonale, à la manière du triangle de Pascal, et on obtient :
$\begin{matrix} 12 & 4 & 3 & 2 & 1 \\ 8 & 1 & 1 & 1 & 1 \\ 7 & 6 & 3 & 1 & 1 \\ 1 & 3 & 3 & 2 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{matrix}$

Il y a $12$ chemins de $A$ à $B$ .

Mihaela J

avril 21, 2023
12h13

Les chemins que vous calculez sont les plus courts (et implicitement qui passent au maximum une seule fois par une case). Le résultat est juste pour ce type de chemin.

Il y en a beaucoup plus si les chemins ne sont pas le plus courts. Encore plus si on laisse repasser par une même case sans passer par la même séparation et encore davantage si on laisse prendre la même séparation.

Connectez-vous pour répondre

Al_louarn

avril 21, 2023
12h25

En effet mais l’énoncé précise qu’on ne peut aller que de gauche à droite et de bas en haut donc il est impossible de repasser par la même case.

Claude

mai 6, 2023
7h50

4e défi

525
Entre 2 et 500, il y a 6 cubes (7³=343) et 21 carrés (22²=484) , le 500° nombre de cette suite est donc 526 auquel il faut retirer 64 qui est compté 2 fois puisque à la fois cube (4³) et carré (8²)

Claude

mai 6, 2023
8h26

Erratum :
il manque 8³=512 (<525) donc le 500° entier est 526

Connectez-vous pour répondre

ROUX

mai 6, 2023
23h23

4e défi
De $2$ à $501$ , il y a $500$ entiers.
$\sqrt{501}$ vaut un peu plus de $22$ donc il y a $22$ carrés à retirer entre $2$ et $501$ . Je peux donc aller désormais jusqu’à $523 = 501 + 22$ .
$\sqrt{523}$ vaut toujours moins de $23$ : je n’ai donc ajouté aucun carré nouveau en allant jusqu’à $523$ .
$\sqrt[3]{523}$ vaut à peine plus de $8$ donc il y a $8$ cubes à retirer entre $2$ et $523$ . Je peux donc aller jusqu’à $531 = 523 + 8$ .
$9^{3} = 729$ donc je n’ajouterai aucun cube avant d’arriver à $729$ .
Par contre, je viens d’ajouter $23^{2} = 529$ que je dois donc retirer puisque je suis arrivé à $531$ .
Donc $532$ me semble être le $500$ ème entier de cette suite.

ROUX

mai 6, 2023
23h25

Ah oui zut $64$ !
Donc plutôt $531$ ?

Connectez-vous pour répondre

ROUX

mai 6, 2023
23h32

4e défi

Ah mince, pas le carré et le cube de $1$ .
Donc alors seulement $21$ carrés et $7$ cubes à retirer donc $501 + 21 + 7 = 529$ . Or $529$ est un carré à retirer donc mon dernier mot sera plutôt $530$ …
Ouille ouille ouille..

pogarreau

mai 8, 2023
12h03

Si l’on cherche la borne supérieure du 500e entier de la suite n’étant ni un carré, ni un cubique ni les 2 à la fois, dans ce cas c’est une puissance de 6. Il faut regarder combien il y a de carrés, de cubes et de puissances 6e.
Pour un intervalle d’entier allant de 1 à N, on a N^1/2 de carrés, N^1/3 de cubes et N^1/6 de puissances 6e environ. Cela donne l’équation suivante : f(N) = N – [N^(1/2)] – [N^(1/3)] + [N^(1/6)] = 500 où les [..] est la partie entière.
Note : on ajoute N^(1/6) pour éviter de soustraire 2 fois les nombres à la fois carrés et cubiques.

Connectez-vous pour répondre

ROUX

mai 8, 2023
13h11

Très joli !!!

Mihaela J

mai 8, 2023
18h02

4e défi

Comme une informaticienne, j’ai fait le code de génération de la suite et le 500ème de la suite est 528.
J’ai implémenté aussi la fonction f de pogarreau : f(528) = 500 et f(527) = 499.

Écrire un commentaire

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .

Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.

Défis de avril 2023

Premier défi

Solution du premier défi

Deuxième défi

Solution du deuxième défi

Troisième défi

Solution du troisième défi

Quatrième défi

Solution du quatrième défi

Post-scriptum

Crédits images

ÉCRIT PAR

Romain Joly

Commentaires

Écrire un commentaire