
Premier défi
Marie a invité \(17\) amis à sa fête d’anniversaire. Elle a attribué à chacun un nombre de \(2\) à \(18\), le \(1\) étant pour elle. Quand tout le monde danse, elle se rend compte que la somme des numéros dans chaque couple est un carré parfait. Quel est le numéro du partenaire de Marie ?


Solution du premier défi
La réponse est : le \(15\)
On observe que la plus grande somme que l’on peut obtenir est \(35 = 17 + 18\), que la plus petite est \( = 1 + 2\) et que les carrés parfaits que l’on peut avoir sont donc \(4, 9, 16\) et \(25\). Donc, le partenaire de Marie peut porter le \(3\), le \(8\) ou le \(15\).
Mais le \(18\) ne peut être en train de danser qu’avec le \(7\), le \(17\) avec le \(8\) et le \(16\) avec le \(9\). On peut ensuite dresser le tableau suivant :
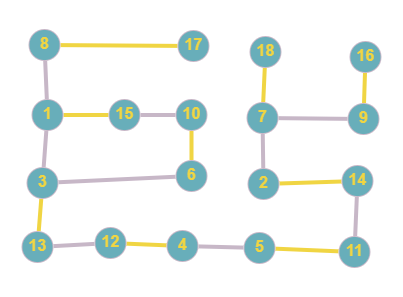
Puisque le \(2\) ne peut danser qu’avec le \(14\), le \(11\) danse forcément avec le \(5\). De ce fait, le \(4\) danse avec le \(12\), et donc le \(13\) danse avec le \(3\). Ainsi, le \(6\) danse avec le \(10\) et le \(1\) avec le \(15\).
Le numéro du partenaire de Marie est donc le \(15\).
Deuxième défi
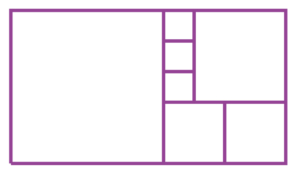
Ce rectangle est divisé en sept carrés. Si l’aire du plus petit carré est de \(1 cm^2\), quelle est l’aire totale du rectangle ?
.


Solution du deuxième défi
La réponse est : \(45 cm^2\).
Les petits carrés sont de côté 1cm, donc celui en haut à droite est de côté \(3 cm\). On en déduit que les deux du bas sont de côté \(2 cm\)et, enfin, que le grand carré est de côté \(5 cm\). Le grand rectangle mesure 9cm sur 5cm et son aire est de \(45 cm^2\).
Troisième défi
L’hypoténuse d’un triangle rectangle mesure \(17 cm\) et son périmètre est de \(40 cm\). Quelle est son aire ?


Solution du troisième défi
La réponse est : \( 60 cm^2\)
On appelle \(a\) et \(b\) les mesures en centimètres des deux autres côtés du triangle. Alors, par le théorème de Pythagore, on a \(a^2+b^2=17^2\).
Par ailleurs, puisque le périmètre mesure \(40 cm\) , on a \(a+b=23\). Donc, on a
$$
\begin{eqnarray*}
(a+b)^2 &=& 23^2\\
a^2+2ab+b^2 &=& 23^2\\
2ab+17^2 &=& 23^2\\
ab&=&\frac{23^2-17^2}{2}\\
ab&=&\frac{(23-17)(23+17)}{2}\\
ab&=& 120 \\
\frac{ab}{2}&=& 60.
\end{eqnarray*}
$$
Quatrième défi
À un goûter, l’âge moyen est égal au nombre de personnes présentes. Lorsque Takéo, qui a 29 ans, arrive à 18h30, l’âge moyen continue de coïncider avec le nombre de présents. Combien de personnes étaient au goûter avant l’arrivée de Takéo ?


Solution du quatrième défi
On note \(x\) le nombre de personnes présentes au goûter avant l’arrivée de Takéo, et on note \(S\) la somme des âges de ces personnes. On a alors \(x=\frac{S}{x}\), donc \(x^2=S\).
Lorsque Takéo arrive au goûter, l’âge moyen continue de coïncider avec le nombre de personnes, c’est-à-dire que l’on a \(x+1=\frac{S+29}{x+1}\), d’où \( (x+1)^2=S+29\).
Comme \(S=x^2\), on obtient
$$
\begin{eqnarray*}
x^2+29 &=& (x+1)^2\\
x^2+29 &=& x^2 +2x+1\\
28 &=& 2x\\
14 &=& x.
\end{eqnarray*}
$$
Il y avait donc \(14\) personnes au goûter.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


9h10
1er défi
L’invité 18 ne peut danser qu’avec l’invité 7. Ainsi le 2 danse nécessairement avec le14, le 11 avec le 5, le 4 avec le 12, le 13 avec le 3, le 6 avec le 10 et le 15 avec Marie ( le 1).
13h41
1er défi
Le 15
Il y a 9 couples dont la somme des n° ne peut être que : 4, 9, 16 ou 25.
Le 18 ne peut aller qu’avec le 7
Le 17 ne peut aller qu’avec le 8
Le 16 ne peut aller qu’avec le 9,
Ensuite vient le 15 avec le 1,
Le 14 avec le 2
Le 13 avec le 3
Le 12 avec le 4
Le 11 avec le 5
Le 10 avec le 6
9h21
2e défi
Il y a quatre tailles de carré : grande, moyenne plus, moyenne moins et petite donc les côtés sont alors respectivement \(G\), \(M\), \(m\) et \(p\).
On a \(M=3p\) et \(M+p=2m\). Donc \(m=2p\).
\(G=3p+m\) ou \(G=5p\)
L’aire \(S\) du rectangle est \(S=G(G+2m)\) ou \(S=5p(5p+2.2p)\) ou \(S=45p^2\).
\(S=45cm^2\)
8h43
3e défi
Si les côtés du triangle sont \(a\),\(b\),\(c\), alors son périmètre est \(p=a+b+c\), d’où :
\(a+b=p-c\)
\((a+b)^2 = (p-c)^2\)
\(a^2 + b^2 + 2ab = (p-c)^2\)
\(2ab = (p-c)^2-(a^2 + b^2)\)
Si \(c\) est l’hypothénuse alors \(a^2+b^2=c^2\) d’après le théorème de Pythagore, donc :
\(2ab= (p-c)^2 – c^2=((p-c)-c)((p-c)+c)=(p-2c)p\)
L’aire du triangle est donc
\[\frac{ab}{2}=\frac{(p-2c)p}{4}=\frac{(40-2\times 17)\times 40}{4}=60\]
9h12
3e défi
Les côtés du triangle rectangle sont \(a\), \(b\) et \(c\) où \(c\) est l’hypoténuse.
\(a^2+b^2=17^2\) par Pythagore.
\(a+b=40-17=23\) par périmètre.
\(2ab=23^2-(a^2+b^2)\) par une identité remarquée.
Comme la surface du triangle rectangle est \(ab/2\) il vient que cette surface est égale à \((23^2-17^2)/4=60\)
9h26
4e défi
Soit x le nombre initial de personnes. L’âge moyen est \(x\), donc l’âge total est \(x^2\).
Avec l’arrivée de Takéo, l’âge total devient \(x^2 + 29\), l’âge moyen \(x + 1\) et le nombre de personnes x + 1.
On a donc \(x^2 + 29 = (x + 1)(x + 1)\), soit \(29 = 2x + 1\).
Il y avait 14 personnes au goûter avant l’arrivée de Takéo.
18h53
3e défi
On pouvait également poursuivre le raisonnement et calculer la longueur des 2 côtés de l’angle droit :
1) données :
H : l’hypoténuse (= 17 cm),
P : le périmètre (= 40 cm),
a et b : les deux autres côtés
2) calcul de l’aire :
a² + b² = 17²
H = 40 – (a + b)
17 = 40 – (x + y)
a + b = 40 – 17
a + b = 23
(a + a)² = 23²
a² + b² + 2ab = 23²
=> système :
| équation #1 : a² + b² + 2ab = 23²
| équation #2 : a² + b² = 17²
équation #1 – équation #2 : 2ab = 23² – 17²
2ab = 529 – 289
2ab = 240
ab = 120
aire = 120/2 = 60 cm²
3) calcul de la longueur de a et de b :
(méthode en passant par une équation du 2e degré)
ab = 120 = P (produit)
a + b = 23 = S (somme)
x² – Sx² + P = 0
x² – 23x² + 120 = 0
delta = 23² – 4*1*120 = 529 – 480 = 49
sqrt(49) = 7
x’ = (-(-23) + 7)/2 = 30/2 = 15 = a
x » = (-(-23) – 7)/2 = 16/2 = 8 = b
ab = 120 = 15*8
a + b = 23 = 15 + 8
4) vérification :
sqrt(8² + 15²) = sqrt(289) = 17 <--- Ok ! :-))