
Premier défi : le problème du mois
Si un tuyau d’orgue de longueur \(\ell\) émet une certaine note, alors un tuyau de longueur \(2\ell\) sonne une octave plus grave et un tuyau de longueur \(\ell\)/\(2\) sonne une octave plus aiguë. Les trois notes portent alors le même nom, par exemple trois do. Combien de noms différents portent les notes émises par un orgue de tuyaux de longueurs 12, 13, 14, . . ., 95 et 96 cm ?


Solution du premier défi
Réponse : \(48\) notes de noms différents.
Deux tuyaux émettent une note de même nom si le rapport de leurs longueurs est une puissance de \(2\).
Numérotons les tuyaux par leurs longueurs et appelons do la note du tuyau de longueur \(12\,{\rm cm}\). Le prochain do est émis par le tuyau \(24\).
Aucune des longueurs intermédiaires n’est deux fois plus petite ou deux fois plus grande qu’une longueur déjà considérée. Il y a donc \(12\) notes différentes pour les tuyaux de \(12\) à \(23\).
Le tuyau \(24=2\times 12\) émet un do une octave plus grave que le premier tuyau. Pour les tuyaux suivants, si le numéro \(n\) du tuyau est pair, alors il émet une octave plus grave que le tuyau \(n/2\) déjà considéré dans la liste et il n’apporte aucun nouveau nom de note. Si le numéro \(n\) est impair, alors aucune note plus aigüe déjà considérée ne porte le même nom car \(n/2\) n’est pas entier.
Il y a \(6\) douzaines entre \(24\) et \(96\) et donc \(6\times 6=36\) numéros impairs. Au total, cet orgue peut produire \(48\) notes de noms différents.
Deuxième défi
Si l’on écrit tous les numéros de page d’un certain livre, on utilise \(2025\) chiffres.
Combien de pages comporte ce livre ?


Solution du deuxième défi
Réponse : \(711\) pages.
Il y a \(9\) nombres strictement positifs à un chiffre, \(90\) nombres à deux chiffres, \(900\) nombres à trois chiffres, etc. Cela montre déjà que le livre comporte moins de \(999\) pages.
Pour écrire les numéros des neuf premières pages, on utilise neuf chiffres.
Pour écrire les numéros des \(90\) pages suivantes, il faut \(90\times 2=180\) chiffres.
Il reste alors \(2025-180-9=1836\) chiffres pour écrire tous les numéros de page à trois chiffres, ce qui donne \(1836 / 3=612\) numéros de page à trois chiffres.
Le livre comporte donc en tout \(9+90+612=711\) pages.
Troisième défi
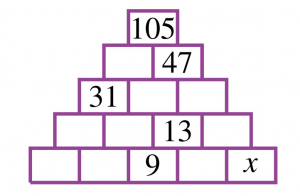
Chaque nombre dans la pyramide est la somme des nombres des cases en dessous de lui (sauf à la base).
Combien vaut \(x\) ?


Solution du troisième défi
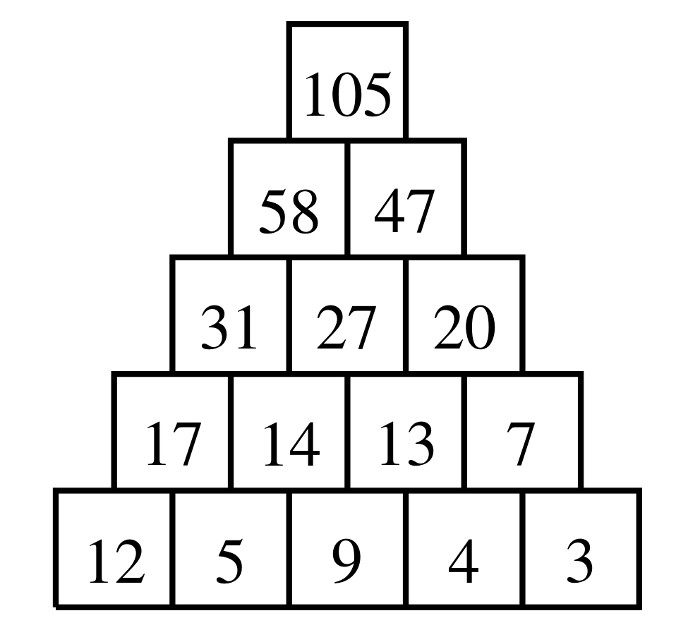
Donnons un nom à chaque nombre, comme sur la figure ci-dessous. Observons que \(a=105-47=58\), \(b=58-31=27\) et \(c=47-27=20\). Comme \(b=27\), on a \(e=27-13=14\). On trouve \(d=31-14=17\) et, comme \(c=20\), on a \(f=20-13=7\).
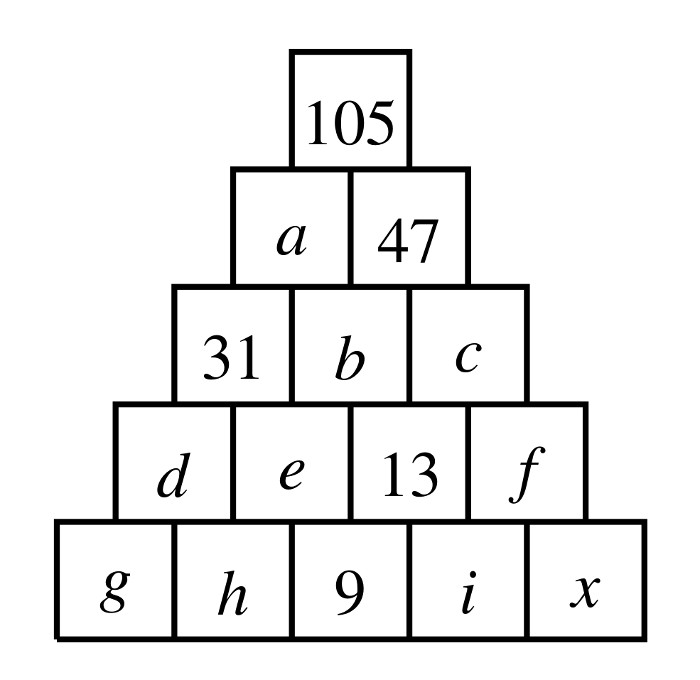
à partir de là, puisque \(i=13-9=4\), on peut déjà trouver la valeur \(x=7-4=3\). Pour compléter la pyramide, on a \(h=14-9=5\) et \(g=17-5=12\).
Quatrième défi
La professeure a écrit l’équation \(x^2+bx+c=0\). Kwami a copié \(b\) correctement, mais s’est trompée en copiant \(c\) et les solutions de son équation sont \(4\) et \(5\). Jean a copié correctement \(c\), mais s’est trompé en copiant \(b\) et les solutions de son équation sont \(2\) et \(4\).
Quelles sont les solutions de l’équation originale ?


Solution du quatrième défi
Réponse : les solutions sont \(x=1\) et \(x=8\).
Comme les solutions de l’équation de Kwami sont \(4\) et \(5\), son équation est \((x-4)(x-5)=x^2-9x+20=0\).
Comme le coefficient \(b\) était correct, alors \(b=-9\) dans l’équation du tableau.
L’équation de Jean est \((x-2)(x-4)=x^2-6x+8=0\). Comme le terme \(c\) est correct, alors \(c=8\) dans l’équation de la professeure.
Ainsi, l’équation du tableau est \(x^2-9x+8=(x-1)(x-8)=0\) et ses solutions sont \(x=1\) et \(x=8\).
Cinquième défi
Si \(n\), \((n+2)\), \((n+6)\), \((n+8)\) et \((n+14)\) sont des nombres premiers, que vaut \(n\)?


Solution du cinquième défi
La réponse est : \(n=5\).
Si le reste de la division de \(n\) par \(5\) est \(1\), alors \(5\) divise \(n+14\). Comme \(n+14>5\) est supposé être premier, c’est impossible. Si le reste est \(2\), alors \(5\) divise \(n+8\) et on obtient encore une contradiction. De même, si le reste est \(4\), \(n+6\) est un multiple de \(5\), ce qui est impossible.
Si le reste de la division de \(n\) par \(5\) est \(3\), \(5\) divise \(n+2\) et donc \(n=3\) est la seule possibilité pour que \(n+2\) soit premier. Mais alors, \(n+6=9\) n’est pas premier, ce qui est une contradiction.
Donc \(5\) divise \(n\), et comme \(n\) est premier, \(n=5\). On vérifie alors que \(n+2=7\), \(n+6=11\), \(n+8=13\) et \(n+14=19\) sont tous premiers.
Ainsi, \(n=5\) est la seule solution.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


15h35
Si on considère la relation d’équivalence \(x \equiv y\) donnée par \(x= 2^k \times y\), le nombre de notes de musique recherchées est égal au nombre de classes d’équivalence entre 12 et 96 inclus.
Par calcul (un programme en Python) on obtient 48.
Par raisonnement :
– il y a 42 nombres impairs \(2k +1\) – on retient donc 42
– les nombres de la forme \(4k +2\) entre 26 et 96 sont générés par multiplication par 2 des impairs – on ne les retient pas
– les nombres de la forme \(4k + 2 \) entre 12 et 24 : 14, 18, 22 ne sont pas dans les classes d’équivalence on les garde (qui correspondent à 7, 9 et 11)
– les nombre de la forme \(4k\) : on ne retient pas ceux à partir de 28 car générés par multiplication par 4
– reste à regarder 12, 16, 20, 24. Or \(24 \equiv 12\). On garde encore 3 classes (qui correspondent à 3, 1 et 5)
Total 48.
Il se peut que je me trompe.
9h57
Si on écarte des nombres entre 12 et 96 tous ceux dont la moitié est aussi entre 12 et 96, il restera exactement un représentant de chaque note. Il s’agit donc de compter les nombres entre 12 et 96 dont la moitié n’est pas un entier entre 12 et 96. Ce sont d’une part les nombres impairs, au nombre de (96-12)/2, et d’autre part les nombres pairs de 12 inclus à 2*12 exclu, au nombre de 12/2.
La réponse est donc (96-12+12)/2 = 48.
9h13
Deuxième défi
Dans un livre de 9 pages, il y a 9 chiffres.
Dans un livre de 99 pages il y a 90 pages de plus, avec 2 chiffres chacune, soit en tout 9 + 90*2 = 189 chiffres.
Dans un livre de 999 pages il y a 900 pages de plus, avec 3 chiffres chacune, soit en tout 189 + 900*3 = 2889 chiffres.
Dans notre livre il y a donc p pages à 3 chiffres, avec p < 900. Il a donc en tout 189 + 3p = 2025 chiffres et 99+p = 99+(2025-189)/3 = 711 pages.
11h54
Troisième défi
En énumérant les lignes de haut en bas, de a à e, et en numérotant les cases de gauche à droite à partir de 1, nous avons par exemple b2 = 47, et e5 = x.
b1 = 105 – 47 = 58, c2 = 58 – 31 = 27, c3 = 47 – 27 = 20, d4 = 20 – 13 = 7, e4 = 13 – 9 = 4, e5 = 7 – 4 = 3 = x.
On peut bien sûr compléter : d2 = 27 – 13 = 14, d1 = 31 – 14 = 27, e2 = 14 – 9 = 5 et e1 = 17 – 5 = 12.
14h05
Si 4 et 5 sont les solutions de l’équation x²+bx+c=0; on a:
(x-4)(x-5)=x²+bx+c
soit x²-9x+20=x²+bx+c d’où
b=-9 et c≠20
Si 4 et 2 sont les solutions de l’équation x²+bx+c=0; on a:
(x-4)(x-2)=x²+bx+c
soit x²-6x+8=x²+bx+c d’où
b≠-6(vrai puisque b=-9 et c=8
L’équation a résoudre est donc:
x²-9x+8
D’où x1=1 et x2=8
17h46
Pour ax²+bx+c =0 et ses deux racines R₁ et R₂
on sait que : R₁+R₂= -b⁄a = -b (a=1)
R₁×R₂= c⁄a = c (a=1)
Avec R₁= 4 et R₂ = 5 (c étant faux), on peut écrire 4+5= 9= -b, d’où b= -9
Avec R₁= 2 et R₂ = 4 (b étant faux), on peut écrire 2×4= 8= c
Le polynôme devient x²-9x+8 = 0
R₁=1 est racine évidente, donc R₂= c⁄R₁= 8/1=8
14h16
Cinquième défi
n, n+2, n+6, n+8, n+14 sont respectivement congrus à n, n+2, n+1, n+3, n+4 modulo 5, donc il y a un multiple de 5 parmi eux, qui est forcément 5 car premier. On écarte n+6, n+8, n+14 trop grands. Ce n’est pas non plus n+2 car on aurait alors n+6 = n+2+4 = 5+4 = 9 non premier. Reste n = 5, qui donne effectivement 5, 7, 11, 13, 19, tous premiers.
La réponse est n = 5.
10h38
n est impair donc il finit par 1,3,5,7 ou 9.
– n ne peut pas finir par 1 car n+14 finirait par 5 donc multiple de 5.
– n ne peut pas être 3 car n+6=9
– n ne peut pas finir par 7 car n+8 finirait par 5 donc multiple de 5.
– n ne peut pas finir par 9 car n+6 finirait par 5 donc multiple de 5.
– n ne peut pas finir par 5 car il serait un multiple de 5.
Seule solution n=5