
Premier défi
Dans la suite 1, 2, 1, 2, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, …, quel est le nombre se trouvant en position 2023?


Solution du premier défi
Réponse : 43.
Remarquons que cette suite de nombres est une succession de « cycles » de plus en plus grands : le premier cycle est la suite \(1,2\) ; le second, la suite \(1,2,3,2\) ; le troisième, la suite \(1,2,3,4,3,2\) ; etc. Il est facile de voir que le
\(i\)-me cycle contient \(2i\) nombres. Ainsi, d’après la formule de Gauss, \(n\) cycles regroupent
\[2+4+6+\cdots+2n = 2\times(1+2+\cdots+n) = n(n+1)\].
Avec \(n=44\), on obtient \(1980\) nombres. Puis, comme le \(45^{\text{e}}\) cycle commence en position \(1981\) et comme \(2023 – 1980 = 43\)
Le nombre se trouvant en position \(2023\) est \(43\).
Deuxième défi
Deux nageuses, placées chacune d’un côté du bassin d’une piscine, démarrent en même temps. La première traverse le bassin en \(45\) secondes, la deuxième en \(30\) secondes. Elles font ainsi des allers-retours durant \(12\) minutes sans s’arrêter. Combien de fois vont-elles se croiser (ou se doubler) durant tout ce temps ?


Solution du deuxième défi
Réponse : \(20\) fois
En \(90\) secondes, les deux nageuses se retrouvent sur le même bord de la piscine et se rencontrent trois fois. Dans les \(90\) secondes suivantes, elles se croisent de nouveau deux fois. Ainsi, en \(180\) secondes, elles se croisent au total \(3+2=5\) fois avant de retrouver leur position initiale. Comme il y a \(720=4\times 180\) secondes dans \(12\) minutes, les deux nageuses se croisent \(4\times 5 = 20\) fois.
Troisième défi
Diviser la figure suivante en quatre parties égales.
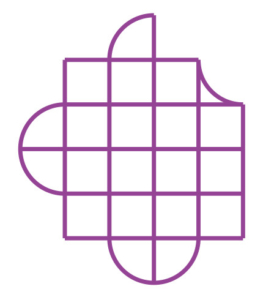


Solution du troisième défi
Une solution est :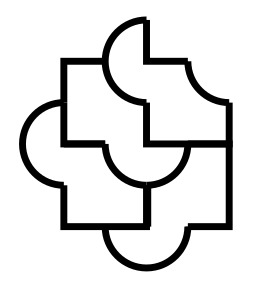
Quatrième défi
Déterminer le nombre de paires \((a,b)\) d’entiers strictement positifs tels que l’équation \(x^3-10x^2+ax-b=0\) d’inconnue \(x\) possède trois solutions entières strictement positives.


Solution du quatrième défi
Réponse : on obtient huit paires d’entiers possibles.
Notons \(r,s\) et \(t\) (avec \(r\le s \le t\)) les trois solutions de cette équation. On a alors la factorisation~:
\[x^3-10x^2+ax-b=(x-r)(x-s)(x-t).\]
En développant cette expression, on obtient~:
\[(x-r)(x-s)(x-t) = x^3-(r+s+t)x^2+(st+tr+rs)x-rst,\]
et en identifiant les coefficients devant \(x^2\), on a~: \(r+s+t = 10\).
Comme ces trois valeurs sont des entiers strictement positifs, le triplet \((r,s,t)\)doit prendre une des valeurs suivantes~: \((1,1,8)\), \((1,2,7)\), \((1,3,6)\), \((1,4,5)\), \((2,2,6)\), \((2,3,5)\), \((2,4,4)\) ou \((3,3,4)\).
Si l’on identifie cette fois-ci les coefficients constants ou devant \(x\), on obtient les égalités
\(a=st+tr+rs\) et \(b=rst\).
Les paires \((a,b)\) qui conviennent sont donc
\((17,8)\), \((23,14)\), \((27,18)\), \((29,20)\), \((28,24)\), \((31,30)\), \((32,32)\) et \((33,36)\).
Par conséquent, on obtient huit paires d’entiers possibles.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


10h10
1er défi
On répartit les éléments de la suite en paquets de telle sorte que le paquet 1 soit 1,2 avec 2 éléments ; le paquet 2 soit 1,2,3,2 avec 4 éléments, … le paquet n soit 1,2,…,n,n+1,n, …,2 avec 2n éléments.
Le dernier élément du paquet n est don en position 2(1+2+…+n)=n(n+1).
Comme 1980=44*45<2023<45*46=2070 l’élément en position 2023 est dans le paquet 45 qui commence en position 1981. Or 2023 -1980 = 43 < 46 l’élément en position 2023 est 43.
13h35
1er défi
En écrivant la suite en spirale sur un quadrillage on voit que pour tout \(n>1\), la deuxième occurence de \(2n+1\) apparaît en position \((2n+1)^2\), précédée des nombres \(1\) à \(2n\). Comme \(2023 = 45^2 – 2\), en position \(2023\) on a \(45 – 2 = 43\).
16h21
Vous êtes notre nouveau Daniate 👍👍👍
16h20
1er défi
Le terme de rang \(\:n^2 + 1 -p\:\), où \(n\) et \(p\) sont des entiers naturels tels que \(p \leq n\), a pour valeur \(\:n + 1 – p\:\). Or \(\:2023=45^2 + 1 – 3\:\) donc le \(2023^\text{ème}\) terme est égal à \(45 + 1 – 3=43\)
23h21
1er défi
Si l’on examine le chiffre 1, on voit qu’il apparaît aux rangs :
1,3,7,13,21,31,43…
On a donc une suite arithmétique de 1° terme U0=1 et de raison 2n.
La forme générale est
Un= U(n-1)+2n soit (après quelques manipulations)
Un=1+n(n+1)
Pour n= 45. Un=1981
Donc le chiffre 1 apparaît au 45° rang de cette suite
Et il apparaîtra de nouveau pour n=46 soit Un= 2071
Entre les 2 rangs il y a donc 90 entiers de 1 à 90
à la valeur 2023, apparaît le 43° entier
7h17
2e défi
Bonjour
Soit A et B les deux positions initiales des filles F1 et F2.
Pendant les 90 premières secondes, F1 fait le trajet A-B-A.
Pendant ce temps, F2 fait le trajet B-A où elle croise F1, puis A-B où elle croise F1 et enfin B-A où elle rattrape F1(donc la double) en A.
Pendant les 90 secondes suivantes, F1 fait le trajet A-B-A.
Pendant ce temps, F2 fait le trajet A-B en distançant F1, puis le trajet B-A où elle croise F1, puis A-B où elle croise F1.
Bilan en 3 minutes, F2 croisent 4 fois F1 et la double une fois et on retrouve la position initiale.
En 12 minutes, les nageuses sont se croiser 16 fois et F2 doublera 4 fois F1.
Cordialement
0h30
2e défi
Soient \(L\) la longueur du bassin, \(O\) l’un de ses bords, et \(P\) et \(Q\) deux points de rencontres consécutives. Entre ces deux rencontres les distances parcourues sont \(PO\) puis \(OQ\) pour l’une, et \(L – PO\) puis \(L – OQ\) pour l’autre, soit au total \(PO + OQ + L – PO + L – OQ = 2L\).
Mais pendant les \(T\) secondes entre deux rencontres, les distances parcourues sont aussi \(\frac{TL}{45}\) pour l’une, et \(\frac{TL}{30}\) pour l’autre.
Donc \(\frac{TL}{45} + \frac{TL}{30} = 2L\), ce qui donne \(T = \frac{2 \times 30 \times 45}{45 + 30} = 36\) secondes.
Ainsi le nombre de rencontres en \(12\) minutes est \(\frac{12 \times 60}{36} = 20\)
16h23
3e défi
Mes 4 tuiles sont identiques, moyennant le retournement d’une d’entre elles. Peut-on faire mieux avec 4 tuiles identiques sans retournement ?
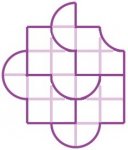
11h30
4e défi
Si on appelle n, m et p les trois solutions entières,
une factorisation du polynôme est
(x-n)(x-m)(x-p)
et un développement est
x^3 – (n+m+p)x^2 +(nm + np + mp)x – nmp.
Par identification des coefficients, il faut avoir
n+m+p = 10
et on a a =nm + np + mp
et b = nmp
On peut avoir 0 < n ≤ m ≤ p. Le tableau ci-après donne tous les cas. 0 < n ≤ m ≤ p avec n + m + p = 10 Cordialement
12h03
4e défi
n m p a b
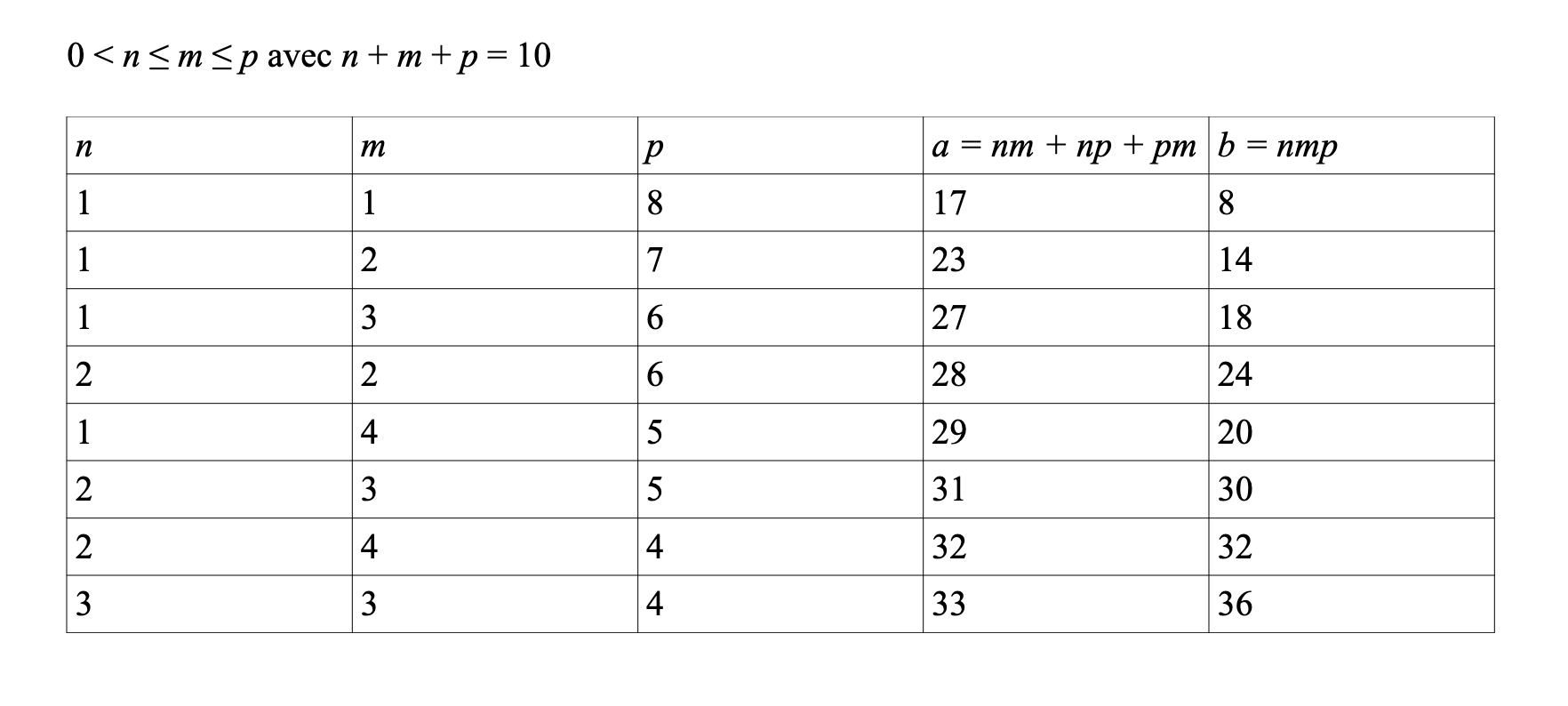
1 1 8 17 8
1 2 7 23 14
1 3 6 27 18
2 2 6 28 24
1 4 5 29 20
2 3 5 31 30
2 4 4 32 33
3 3 4 33 36
18h42
4e défi
Voici comment trouver combien il y a de paires (a,b) sans faire trop de calculs, vive la farniente estivale ! (8,17)
On factorise le polynôme (x-m)(x-n)(x-p)=0 avec ses trois racines entières 0
(2,3) ; (7,8) ; (14,9) —> (14,23)
(3,4) ; (6,7) ; (18,9) —> (18,27)
(4,5) ; (5,6) ; (20,9) —> (20,29)
(4,4) ; (12,8) —> (24,28)
(6,5) ; (10,7) ; (15,8) —> (30,31)
(8,6) ; (16,8) —> (32,32)
(9,6) ; (12,7) —> (36,33)