
1er défi
Avec \(100\) cartes numérotées de \(1\) à \(100\), on doit former des paquets de trois cartes de sorte que dans chaque paquet, le nombre d’une des cartes soit le produit des deux autres. Par exemple \(\{3, 32, 96\}\) est un tel paquet. Quel est le nombre maximal de paquets que l’on peut former ?


Solution du 1er défi
Réponse : huit paquets
Notons \(a\), \(b\) et \(c\) les nombres sur les trois cartes d’un paquet tels que \(ab=c\) et \(1\leq a<b<c\leq 100\).
Commençons par observer que \(a=1\) est impossible car, sinon, \(b=c\).
Par ailleurs, on doit avoir \(a^2 < ab=c\leq 100\). Donc \(a<\sqrt{100}=10\) et \(a\) est entre \(2\) et \(9\).
Ainsi, on pourra former au maximum huit paquets, un avec chacune des valeurs possibles de \(a\). Une possibilité est de former les paquets : \(\{9,11,99\}\), \(\{8,12,96\}\), \(\{7,13,91\}\), \(\{6,15,90\}\), \(\{5,17,85\}\), \(\{4,21,84\}\), \(\{3,26,78\}\) et \(\{2,34,68\}\).
2e défi
Sur un échiquier, on pose huit reines noires sur la première ligne et huit blanches sur la dernière. On les fait bouger une à la fois, horizontalement, verticalement ou en diagonale, d’autant de cases que l’on veut, à condition qu’il n’y ait pas d’autre reine sur le chemin. Quel est le nombre minimal de mouvements à effectuer pour échanger les deux lignes ?


Solution du 2e défi
Réponse : 23 mouvements.
Numérotons les colonnes de A à H et les lignes de 1 à 8.
Alors, (A1−A2), (H8−A1), (H1−H8), (A8−H1), (A2−A8), (B1−F5), (C1−F4), (B8−B1), (C8−C1), (F4−B8), (F5−C8), (F1−C4), (G1−C5), (F8−F1), (G8−G1), (C4−G8), (C5−F8), (D1−H5), (E1−A5), (D8−D1), (E8−E1), (H5−E8) et (A5−D8) donnent une solution en 23 mouvements.
Montrons que 23 est le minimum.
Chacune des 16 reines doit bouger au moins une fois. Des quatre reines qui sont dans les coins, trois au maximum ne pourront être bougées qu’une fois, donc on aura besoin d’un mouvement supplémentaire. Et, en ce qui concerne les reines opposées sur chaque colonne, seulement une des deux, au plus, ne pourra être bougée qu’une fois. Cela ajoute encore six mouvements, ce qui fait un total minimal de 16+1+6=23 mouvements.
3e défi
Si le côté vertical du rectangle mesure 1cm, combien mesure son côté horizontal ?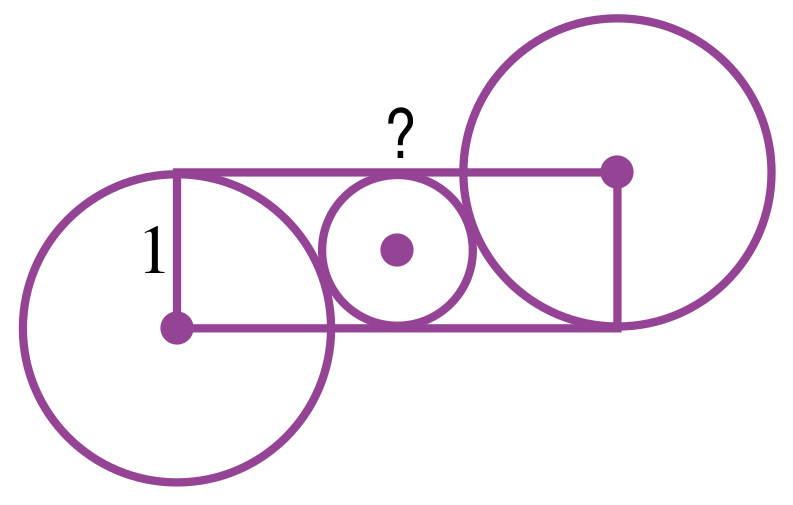


Solution du 3e défi
Réponse : \(2\sqrt 2\,\textrm{cm}\).
On trace le segment qui relie les centres des grands cercles. Alors la diagonale du rectangle obtenue est formée de deux grands rayons et deux petits rayons. Elle mesure donc \(3\,\textrm{cm}\) puisque le rayon du petit cercle mesure \(\frac{1}{2}\,\textrm{cm}\) et le rayon du grand cercle mesure \(1\,\textrm{cm}\).
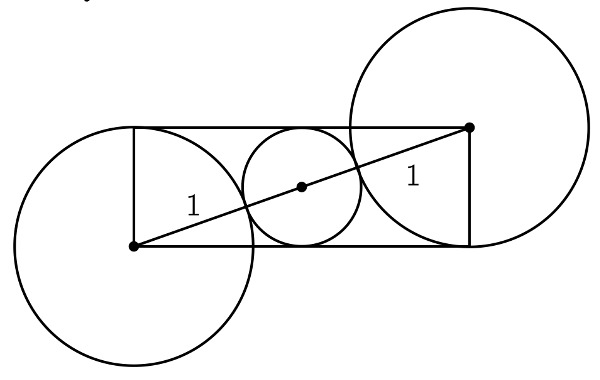
En notant \(x\) la longueur du côté horizontal du rectangle, par le théorème de Pythagore, on a \(x^2=3^2-1^2=8\), donc \(x=2\sqrt 2\,\textrm{cm}\).
Ainsi, le côté horizontal mesure \(2\sqrt 2\,\textrm{cm}\).
4e défi
Le premier chiffre d’un nombre à quatre chiffres (donc le chiffre des milliers) est le nombre de chiffres 0 qui apparaissent dans ce nombre, le deuxième chiffre est le nombre de 1, le troisième chiffre est le nombre de 2 et le dernier chiffre est le nombre de 3. Quels nombres à quatre chiffres vérifient ces conditions ?


Solution du 4e défi
Réponse : les deux nombres possibles sont \(2020\) et \(1210\).
Remarquons que le premier chiffre (chiffre des milliers) doit être inférieur ou égal à \(3\) et strictement supérieur à \(0\).
Si c’est \(3\), alors les autres chiffres doivent être \(0\), mais ce n’est pas possible car le dernier chiffre représente la quantité de \(3\), qui devrait alors être \(1\).
Si le premier chiffre est \(2\), alors il y a deux \(0\) et le troisième chiffre doit être au moins \(1\). Mais ce ne peut pas être \(1\) car les autres chiffres valent \(0\) et le deuxième indique la quantité de \(1\). La seule solution est alors \(2020\).
Maintenant, si le premier chiffre est \(1\), alors le deuxième est supérieur à \(1\), et comme on peut mettre un seul chiffre \(0\), la seule solution est alors \(1210\).
5e défi
Placer les nombres \(1, 1, 2, 2, 2, 3, 4, 5, 7\) et \(8\), de sorte que le produit des sommets de chaque triangle donne le nombre écrit à l’intérieur.
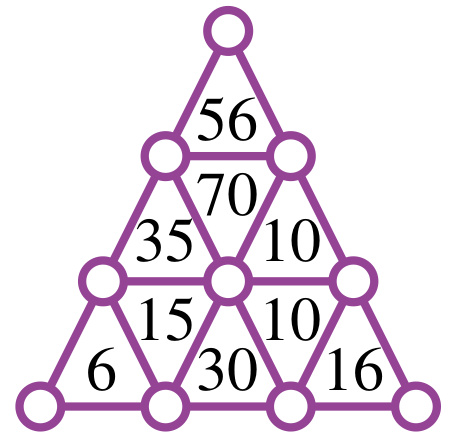


Solution du 5e défi
Remarquons que \(35=7\times 5\times 1\). Comme \(5\) ne divise pas \(56\), dans le sommet en commun à \(35\) et \(56\), il faut mettre \(1\) ou \(7\). Si l’on y met \(1\), on aurait alors besoin de deux \(7\) : un pour compléter le triangle dont les sommets ont pour produit \(35\), et l’autre pour compléter celui dont le produit donne \(56\). Finalement, on met le \(7\) entre \(35\) et \(56\). On place alors \(5\) entre \(35\), \(70\) et \(15\), et \(1\) dans le sommet restant pour obtenir \(35\). Les autres nombres se placent ensuite un par un pour obtenir les produits souhaités. On aboutit à :
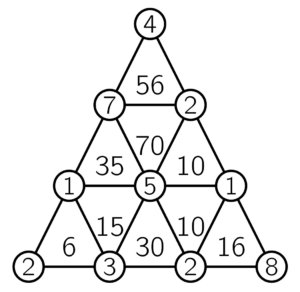
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock





14h19
1er défi
Bonjour
Soit a, b et c les trois cartes d’un paquet avec a < b < c. On veut donc axb = c et on a a^2 < c < 101 , donc a <= 10. Le cas a = 10 est impossible car on aurait au minimum b = 11 et c = 110. Le cas a = 1 est impossible car on aurait b = c. a peut donc prendre 8 valeurs entre 2 et 9 et donc 8 tas possibles au maximum. Par exemple : 9 x 11 = 99 8 x 12 = 96 7 x 14 = 98 6 x 15 = 90 5 x 19 = 95 4 x 23 = 92 3 x 31 = 93 2 x 47 = 94 Cordialement
17h02
1er défi
Alors, de 2∗3=6 à 2∗50=100, ça fait 50−3+1=48 paquets possibles.
3∗4=12 à 3∗33=99, ça fait 33−4+1=30 paquets possibles.
4∗5=20 à 4∗25=100 ça fait 25−5+1=21 paquets possibles.
5∗6=30 à 5∗20=100 ça fait 20−6+1=15 paquets possibles.
6∗7=42 à 6∗16=96 ça fait 16−7+1=10 paquets possibles.
7∗8=56 à 7∗14=91 ça fait 14−8+1=7 paquets possibles.
8∗9=72 à 8∗12=96 ça fait 12−9+1=4 paquets possibles.
9∗10=90 à 9∗11=99 ça fait 11−10+1=2 paquets possibles.
On a au total 48+30+21+15+10+7+4+2=137 paquets possibles.
17h15
Bonjour
Ha, oui pour votre réponse, mais j’avais pensais à des paquets en même temps.
Cordialement
19h48
Ah ok !!!
C’est peut-être vous qui avez raison…
J’ai peut-être mal compris la question…
La question est plus belle avec votre réponse 🙂
21h48
1er défi
Je n’ai pas la solution mais le problème me semble beaucoup plus complexe car on veut déterminer le nombre maximal de paquets ayant la propriété mais quand on a utilisé des cartes pour former un paquet, les nombres correspondant à ces cartes ne peuvent plus être ré-utilisés pour former de nouveaux paquets.
22h12
1er défi
La carte 1 est exclue du partitionnement car aucun triplet ayant la propriété ne peut la contenir.
Il faut donc raisonner sur 99 cartes (2 à 100).
Avec 99 cartes et sans aucune considération sur les paquets formés, on ne peut former au maximum que 99 / 3 = 33 paquets de trois cartes.
Le nombre recherché est donc inférieur à 33.
Propriétés intéressantes à exploiter peut-être :
le produit maximum ne peut pas dépasser 100,
le nombre de plus grand de chaque triplet puisqu’il est le produit des deux autres nombres ne peut pas être un des nombres premiers entre 2 et 100.
13h44
1er défi
Les triplets que nous cherchons sont de la forme (a, b, ab).
a et b ne peuvent être tous les deux supérieurs ou égal à 10.
Sans perte de généralité considérons que a est le plus petit nombre ; il ne peut donc varier qu’entre 2 et 9 soit 8 valeurs possibles (1 est exclu car il ne peut pas faire partie d’un triplet ayant la propriété recherchée).
Le nombre maximum recherché est donc inférieur ou égal à 8.
L’ensemble contenant les triplets (9, 11, 99), (8, 12, 96), (7,14, 98), (6,15, 90), (5, 19, 95), (4, 22, 88), (3, 28, 84) et (2, 29, 58) possède 8 éléments.
Le nombre recherché est donc égal à 8.
15h41
2e défi
Il est évident que chaque reine doit faire au moins un déplacement, et que si c’est le cas elle prend la place d’une reine adverse, avec laquelle elle est donc en prise au départ.
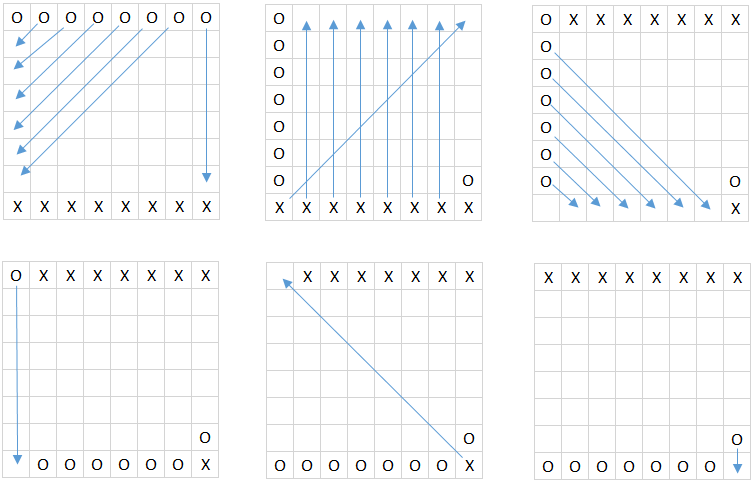
Considérons une paire de reines adverses se faisant face et non situées dans les coins. Chacune est en prise avec l’autre et aucune autre, donc pour qu’elles arrivent en un coup chacune dans la ligne adverse il faut les permuter en \(2\) coups, ce qui est impossible. Donc il faut au moins \(3\) coups pour traiter chacune des \(6\) paires concernées, soit \(18\).
Considérons maintenant les \(4\) reines en coin. Chacune est en prise avec les \(2\) reines des coins adverses et aucune autre, donc pour
15h44
Ah ben si ça marche 🙂
8h24
3e défi
Les deux grands cercles ont pour rayon 1 et le petit cercle a pour diamètre 1.
Les grands cercles étant tangents au petit, la diagonale du rectangle a pour longueur 2 rayons de grand cercle et un diamètre de petit cercle soit 3.
En appliquant le théorème de Pythagore, on a le grand côté du rectangle qui vaut racine carrée de 8 ( ou 2 racine carré de 2).
15h54
4e défi
La somme des chiffres est forcément 4 puisqu’ils dénombrent 4 chiffres différents.
L’un est nécessairement 0 puisque le chiffre des milliers est forcement non nul.
3 ne peut pas un des chiffres puisque la somme est alors multiple de 3.
Reste 0+2+2 qui donne 2020 ou 1 + 1 + 2 qui donne 1210
19h39
Rphino
Bonjour
Surpris par votre réponse 1210 quand l’énoncé stipule « le dernier chiffre est le nombre de 3. » !!
Cordialement
19h42
J’ai écrit une bêtise et je ne sais pas effacer.
9h54
4e défi
Les nombres recherchés sont de la forme abcd (en notation décimale).
a ne peut prendre que les valeurs 1, 2 ou 3 (le zéro est exclu car sinon le nombre n’est pas à quatre chiffres ; les valeurs supérieures ou égales à 4 sont exclus car sinon il y aurait plus de 0 que de chiffres dans le nombre.
Si a = 1, il y a un zéro parmi les trois autres chiffres.
On ne peut pas avoir b = 0 car il y a au moins un 1.
On a donc soit c = 0 soit d = 0
Cas c = 0 alors n = 1b0d
b est différent de 0 (un seul 0), de 1 (s’il vaut 1, il y aurait un seul 1 alors qu’il y en a deux) et de 2 (pas de 2 dans le nombre). De même pour les valeurs 3 et 4 donc pas de solution dans ce cas.
Cas d = 0 alors n = 1bc0 ; b et c ne peuvent prendre que les valeurs 1 ou 2.
b = 1 est impossible (nb de 1 incompatibles) ; b = 2 alors c = 2 (impossible) donc pas de solution aussi dans ce cas.
Si a = 2, il y a deux zéros et donc au moins un 2 ; la seule possibilité est c = 2 donc n = 2020
Si a = 3 alors il ya trois zéros donc n = 3000 ; ce nombre ne remplit pas la condition d = 1 (il contient un 3).
Il n’y a donc qu’un seul nombre qui remplit toutes les conditions (2020).
8h58
Vous écartez trop rapidement 1 2 1 0. Faites le compte, ça marche.
16h25
5e défi
5 est dans le seul cercle à l’intérieur car les six nombres qui l’entourent sont tous multiples de 5.
7 est commun à 35, 70 et 56.
Ensuite tout se détermine sans aucune difficulté puisqu’on a toujours un triangle duquel on connait les valeurs de deux sommets et auquel il manque donc la dernière valeur univoque.
Pourquoi ne nous a-t-on pas seulement demandé de remplir les cercles avec des entiers positifs ?