
Premier défi : le problème du mois
Si chaque lettre représente un chiffre différent, quel est le résultat de la multiplication ci-dessous ?
\begin{array}{ccccc}
& & 1 & A & E\\
\times & & E & 1 & E\\
\hline
& & B & D & F\\
& 1 & A & E & \\
B & D & F & & \\
\hline
B & E & E & E & F \\
\end{array}


Solution du premier défi
De la quatrième colonne de cette multiplication, on déduit que \(D + E = E\), soit \(D = 0\).
Si \(E=1\), alors la troisième colonne \(B+A+F\) doit donner une somme se terminant par \(1\) et doit donc engendrer une retenue qui, additionnée avec \(1+D=1\), doit se terminer par \(E=1\), ce qui est impossible.
On déduit donc de la seconde colonne que \(E = 2\) ou \(E = 3\), puisque la retenue de \(B+A+F\) vaut \(1\) ou \(2\). Du fait que \(1AE\times E = BDF\) et \(E^2<10\), on sait que le chiffre des unités de \(E\times A\) vaut \(0\), ce qui implique que \(E = 2\) et \(A=5\).
Par la dernière colonne, on a donc \(F=E^2 = 4\). En prenant les deuxième et troisième colonnes de cette multiplication, on a enfin \(B+5+4= 12\), autrement dit \(B = 3\).
Donc la multiplication est :
\(
\begin{array}{ccccc}
& & 1 & 5 & 2\\
\times & & 2 & 1 & 2\\
\hline
& & 3 & 0 & 4\\
& 1 & 5 & 2 & \\
3 &0 & 4 & & \\
\hline
3 & 2 &2 & 2 & 4
\end{array}
\)
Deuxième défi
En tournant un cube de droite à gauche, face à soi, on peut y lire le mot “RARE”.
Quelle est la position des lettres R et E dans le patron dessiné ci-dessous ? 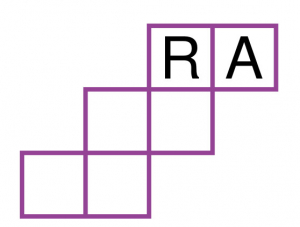


Solution du deuxième défi
On obtient le patron suivant:
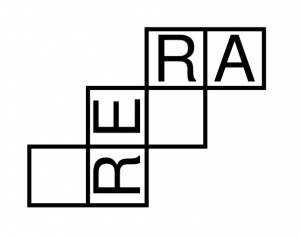
Troisième défi
On note respectivement \(S(n)\) et \(P(n)\) la somme et le produit des chiffres de l’entier \(n\).
Par exemple, \(S(23)=5\) et \(P(23)=6\).
Si \(N\) est un nombre à deux chiffres tel que \(N=S(N)+P(N)\), quel est le chiffre des unités de \(N\) ?


Solution du troisième défi
Si l’on note respectivement \(a\) et \(b\) les chiffres des dizaines et des unités de \(N\), alors \(N=10a+b\) et la condition \(N=S(N)+P(N)\) devient \(10a+b=a+b+ab.\)
On obtient ainsi \(a(b-9)=0 .\)
Mais comme \(a\neq 0\), puisque \(N\) est un nombre à deux chiffres, il suit que \(b-9=0,\) autrement dit \(b=9 .\)
Quatrième défi
Deux cercles de rayons respectifs \(3\,{\rm cm}\) et \(8\,{\rm cm}\) sont touchés par une tangente commune aux points \(C\) et \(D\). Sachant que \((AB)\) et \((CD)\) se croisent en \(E\) et que \(AE=5\,{\rm cm},\) quelle est la longueur de \([CD]\)?
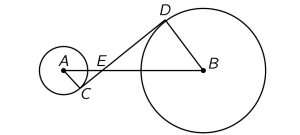
.


Solution du quatrième défi
On a \(\widehat{AEC}=\widehat{BED}\) (car ce sont des angles opposés par le sommet)
et \(\widehat{ACE}=\widehat{BDE}=90^{\circ}\) (car la droite \((CD)\) est tangente aux cercles en \(C\) et \(D\)) : les triangles \(AEC\) et \(BED\) sont donc semblables.
On en déduit que \(\frac{CA}{BD}=\frac{3}{8}=\frac{CE}{ED}\).
En appliquant le théorème de Pythagore dans le triangle \(ACE\), on obtient \(CE=4\,{\rm cm}\). Il suit que \(\frac{4}{ED}=\frac{3}{8}\), donc \(ED=\frac{32}{3}\,{\rm cm}\). On obtient donc \(CD=\frac{32}{3}+4=\frac{44}{3}\,{\rm cm}\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h49
1er défi
A = 5 et E =2.
E = 1 n’est pas possible car F différent de E.
On passe ensuite à E = 2 et on voit qu’il n’y a pas d’autre possibilité que A = 5.
Le résultat est donc: 32224
8h58
(on vérifie tout de même que les lettres correspondent à des chiffres deux à deux distincts (B = 3, F = 4 et D = 0)).
11h44
1er défi
Deuxième colonne sans retenue possible: \(D+E=E\) impose que \D\) vaut \(0\).
Quatrième colonne: la retenue maximale issue de la troisième colonne est \(2\) donc \(E\) vaut au maximum \(3\). Dans la table de multiplication de \(E\) il faut réussir avec \(A\) à faire un \(0\).
La seule possibilité est alors \(E=2\) et \(A=5\) c
Le reste découle.
10h13
2e défi
On note les faces de la manière suivante:
1 2
3 4
5 6
Dans ce cas, la face 3 vient à côté de la 1: elle correspond au E.
La face 6 vient en face de la face 1: elle correspond donc au R.
20h38
On peut préciser que le R et le E subissent une rotation sur la gauche de 90°.
13h14
3e défi
N = 10d + u = d + u + ud
On obtient donc 9d = ud
Soit, comme d est différent de 0, u = 9.
remarque: il n’y a pas de condition sur d donc tous les nombres dont l’écriture décimale est de la forme ‘x9’ conviennent (x différent de 0)
17h16
3e défi
\(N = 10d + u = d + u + ud\)
15h55
4e défi
Pour les triangles \(AEC\) et \(BED\), les angles en \(C\) et \(D\) sont droits donc égaux, et les angles en \(E\) sont égaux, donc les angles en \(A\) et \(B\) sont encore égaux. Ainsi ces triangles sont semblables, ce qui implique \(\frac{ED}{EC} = \frac{BD}{AC} = \frac{8}{3}\), d’où \(ED = \frac{8}{3}EC\).
Or \(CD = EC+ED\) donc \(CD = EC+\frac{8}{3}EC = \frac{11}{3}EC\).
Pour le triangle \(AEC\) rectangle en \(C\) le théorème de Pythagore donne \(EC^2 + AC^2 = AE^2\), d’où \(EC^2 = AE^2 – AC^2 = 5^2 – 3^2 = 16 = 4^2\), soit \(EC = 4\) et finalement \(CD = \frac{44}{3}\).
17h45
4e défi
Une tangente à un cercle est perpendiculaire au rayon de ce cercle qu’elle touche et deux droites perpendiculaires à une même troisième sont parallèles entre elles.
Donc \((AC)//(BD)\).
On peut donc faire des thalesseries.
Le triangle \(ACE\) est rectangle en \(C\) et les valeurs de ses côtés sont celles du fameux triangle rectangle minimal qui génèrent toutes les équerres dans le bâtiment: mon tonton plâtrier clouait rapidement le \(60=3*20_80=4*20_100=5*20\).
Donc \(CE=4\)
Alors \(ED/DB=EC/AC\) ou \(ED=8*4/3=32/3\)
\(CD=CE+ED=4+32/3=12/3+32/3=44/3\)