
1er défi
Les entiers \(22\) , \(23\) et \(24\) ont la propriété que tous les exposants qui apparaissent dans leurs décompositions en produits de facteurs premiers distincts sont impairs, puisque \(22=2^1\times 11^1\), \(23=23^1\) et \(24=2^3\times 3^1\). Quelle est la longueur maximale d’une suite d’entiers consécutifs ayant cette propriété ?


Solution du 1er défi
La réponse est : 7.
Observons que l’on pourrait ajouter \(21=3^1\times 7^1\), mais ni \(20\) ni \(25\) ne conviennent.
En continuant avec les entiers qui suivent, on trouve la suite
\(29=29^1\), \(30=2^1\times 3^1\times 5^1\), \(31=31^1\), \(32=2^5\), \(33=3^1\times 11^1\), \(34=2^1\times 17^1\) et \(35=5^1\times 7^1\), ce qui donne une suite de sept nombres consécutifs. Cette suite ne peut être prolongée car ni \(28=2^2\times 7\) ni \(36=2^2\times3^2\) ne conviennent.
Montrons que ce phénomène d’obstruction est général et que la longueur maximale d’une telle suite est \(7\). Parmi huit entiers consécutifs, l’un est toujours de la forme \(8n+4\) ou bien \(8n-4\). Or un tel nombre est divisible par \(4=2^2\)et non par \(8=2^3\). On en déduit qu’il y a au maximum sept nombres consécutifs vérifiant la propriété demandée.
2e défi
Un certain polygone régulier possède trois fois plus de diagonales que de côtés. Combien a-t-il alors de côtés ?


Solution du 2e défi
La réponse est : 9 côtés.
Si le polygone a \(n\) côtés, il a donc
\({ n \choose 2} – n = \frac{n!}{2!(n-2)}-n = \frac{n(n-1)}{2}-n=\frac{n(n-3)}{2} \) diagonales.
En effet, il y a \( n \choose 2 \) façons de choisir deux sommets à relier parmi \(n\), mais on obtient ainsi non seulement toutes les diagonales mais aussi les \(n\) côtés (obtenus lorsque les sommets sont adjacents).
Il s’agit donc de résoudre l’équation \(\frac{n(n-3)}{2}=3n\). Elle est équivalente à \(n^2-3n=6n\) ou encore à \(n(n-9)=0\).
Cette équation possède une seule solution strictement positive, à savoir \(n=9\). Le polygone a donc neuf côtés.
3e défi
Placer les nombres de 1 à 9 dans la grille de sorte que le produit des nombres de chaque ligne et de chaque colonne soit égal au résultat affiché en fin de ligne ou colonne.
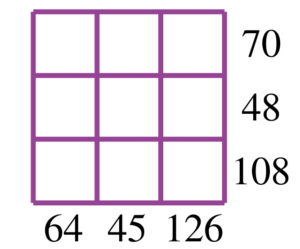
.


Solution du 3e défi
Considérons la première colonne. Comme \(64=2^6\), les nombres dans la première colonne doivent être \(2\), \(4\) et \(8\). Le même raisonnement montre que la deuxième colonne, dont le produit vaut $45$, contient les nombres \(1\), \(5\) et \(9\). La troisième colonne contient donc les nombres \(3\), \(6\) et \(7\).
Analysons maintenant les lignes. La première ligne, dont le produit vaut \(70=2\times 5 \times 7\), doit contenir les nombres \(2\), \(5\) et \(7\). Pour la deuxième, comme \(48=2^4\times 3\), elle doit contenir \(1\), \(6\) et \(8\). Finalement, le carré complété est le suivant~:
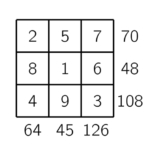
.
4e défi
Un triangle \(ABC\) est rectangle en \(B\) et vérifie \(AB=3\,\mathrm{cm}\) et \(AC=5\,\mathrm{cm}\). La bissectrice issue de \(A\) recoupe le segment \([BC]\) en un point \(D\). Que vaut \(\frac{BD}{DC}\) ?


Solution du 4e défi
La réponse est \(\frac {3} {5}\).
Traçons la perpendiculaire à \((AC)\) passant par \(D\). Elle recoupe le segment \([AC]\) en un point \(E\).
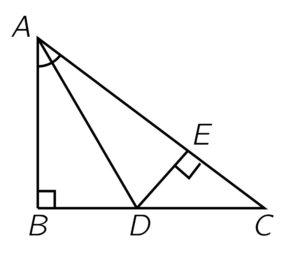
.
Comme \((AD)\) est la bissectrice de \(\widehat{BAC}\), on a \(BD=DE\). De plus, les triangles \(ABC\) et \(DEC\) ont les mêmes angles et sont donc semblables. Par conséquent,
$$ \frac{BD}{DC} = \frac{DE}{DC} = \frac{AB}{AC} = \frac {3} {5}$$
5e défi
Comment choisir deux nombres de l’ensemble \(\{1,2,3,\ldots, 17\}\) de sorte que leur produit soit égal à la somme des \(15\) nombres restants~?


Solution du 5e défi
Solution : les nombres \(10\) et \(13\).
La somme des entiers de \(1\) à \(17\) vaut \(153\).
Si \(a\) et \(b\) sont deux entiers qui conviennent, on a doit avoir
\[1+2+\cdots +17 -a -b = ab.\]
Cette équation est équivalente à \[ab+a+b=153,\] ou encore à
\[(a+1)(b+1)=154.\]
On en déduit que les nombres \(a+1\) et \(b+1\), compris entre \(2\) et \(18\), sont des diviseurs de \(154\). Ces diviseurs sont \(2\), \(7\), \(11\) et \(14\), et la seule paire de diviseurs qui convient est donc \(\{11,14\}\).
On obtient alors, pour \(a\) et \(b\), les nombres \(10\) et \(13\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h23
1er défi
Voici une suite de \(7\) nombres consécutifs avec la propriété demandée :
\(29=29^1\)
\(30=2^1 \times 3^1 \times 5^1\)
\(31=31^1\)
\(32=2^5\)
\(33 = 3^1 \times11^1\)
\(34 = 2^1 \times 17^1\)
\(35 = 5^1 \times 7^1\)
On ne peut pas faire mieux que \(7\) car une telle suite se trouve forcément entre deux nombres \(2^2(2n+1)\) et \(2^2(2(n+1)+1)=2^2(2n+1)+8\), dans lesquels l’exposant de \(2\) est \(2\) donc pair.
19h02
1er défi
Dans une suite d’entiers ayant cette propriété et ayant plus de \(4\) éléments, il y en a un divisible par 4 (au pire le \(4^{ième}\). Il s’écrit \(n=4*2^{1+2\alpha}q\) avec \(\alpha\ge0\) et \(q\) impair.
Or \(n+4=4(2^{1+2\alpha}q+1)\) et \(2^{1+2\alpha}q+1\) est impair donc ne fait pas partie de la suite. Donc la suite contient au plus \(\{n-3, n-2, n-1, n, n+1, n+2, n+3\}\) soit \(7\) éléments. Al_louarn nous fournit une telle suite de 7 éléments.
8h14
2e défi
Si le polygone a \(n\) côtés alors il a autant de sommets et donc on peut former \({ n \choose 2} = \frac{n(n-1)}{2}\) couples de sommets. Ces couples sont les extrêmités de segments, dont \(n\) sont les côtés du polygone, et les autres sont les diagonales. Ainsi :
\(\frac{n(n-1)}{2} – n = 3n\)
\(\frac{n(n-1)}{2} = 4n\)
\(n-1 = 8\)
\(n = 9\)
8h18
2e défi
Soit n le nombre de côté alors n=9
En calculant le nombre de diagonales des premiers polygones, on obtient :
N=3 —> d(nbre de diagonales)=0
N=4 —>d=2
N=5 —>d=5
N=6 —>d=9
N=7 —>d=14
On devine une suite de la forme :
d(n)=d(n-1)+[d(n-1)-d(n-2)+1]
Soit d(n)=2d(n-1)-d(n-2)+1
On voit rapidement que pour n=9
d(9)=2d(8)-d(7)+1=(2×20)-14+1=27
13h47
2e défi
On obtient également le resultat d’une manière moins intuitive, En développant la suite
d(n)=2d(n-1)-d(n-2)+1
On obtient dn=d(n-1)+ n-2
Suite qu’on peut encore améliorer pour obtenir dn uniquement en fonction de n :
dn=( n-2)+(n-3)+(n-4)+…+4+3+2
Soit en réduisant :
dn=n(n-3)/2
Et pour dn=3n
3n=n(n-3)/2 —> n=9
10h02
2e défi
Un polygone régulier à n côtés possède n * (n – 3) / 2 diagonales.
Il suffit donc de résoudre l’équation :
n * (n – 3) / 2 = 3 * n
soit : n^2 – 3 * n = 6 * n
en simplifiant par n on obtient n -3 = 6
donc n = 9
8h17
3e défi
1ère ligne : 2 – 5 – 7
2ème ligne : 8 – 1 – 6
3ème ligne : 4 – 9 – 3
11h33
3e défi
\(70\cap45=5\) pour la divisibilité par \(5\) de ces deux nombres.
\(70\cap64=2\) pour la divisibilité par \(2\) de ces deux nombres.
\(70\cap126=7\) pour le \(7\) restant de \(70\).
Et ainsi de suite.
10h03
4e défi
On projette \(D\) sur la droite \( (AC) \) en un point \(H \). Comme \((AD)\) est la bissectrice issue de A on a \(BD = DH\). Les triangles \(ABC\) et \(DHC\) sont semblables (vieille notion) car il ont deux angles égaux :
\( \frac{DH}{DC}=\frac{AB}{AC} \) et donc \( \frac{BD}{DC}=\frac{3}{5}\).
11h14
4e défi
On note \(2x\) la mesure de l’angle \(BAC\).
En exprimant les aires des triangles \(ABD\) et \(ADC\) de deux manières on obtient :
\[ \frac{1}{2} BD \times AB = \frac{1}{2} AB \times AD \times \cos{x} \]
\[ \frac{1}{2} CD \times AB = \frac{1}{2} AD \times AC \times \cos{x} \]
On fait le rapport des égalités et on obtient :
\[\frac{BD}{CD} = \frac{AB}{AC}\]
Le rapport recherché vaut \( \frac{3}{5}\).
0h57
3e défi
La décomposition de chaque produit en facteurs premiers fut une aide indéniable pour remplir cette grille. Et ceci rend le défi très intéressant. Je ne sais pas cependant s’il existe un moyen de trouver la bonne disposition des nombres de 1 à 9 avec une méthode qui ne laisserait aucune place aux hypothèses du hasard.
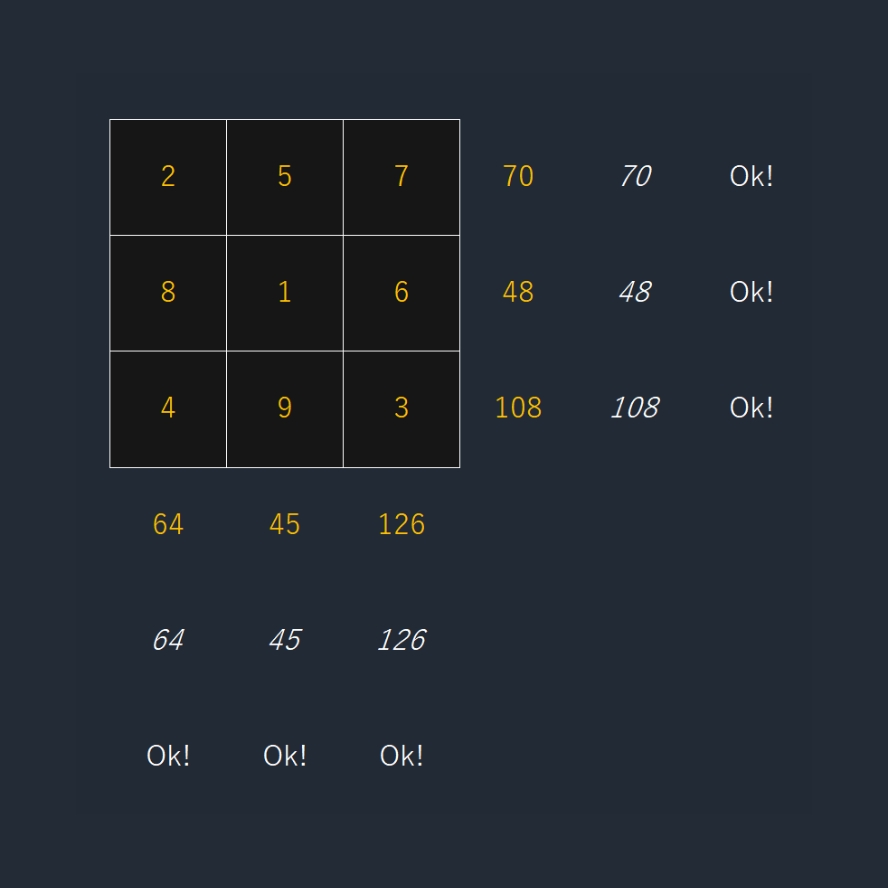
18h18
3e défi
Oui, en effet, on peut.
Seuls 70 et 45 ont 5 comme diviseur commun et seuls 70 et 126 ont 7 en commun.
J’appellerai chaque ligne et chaque colonne par le produit des nombres y figurant et les points indiqueront un nombre manquant.
Posons donc tout d’abord :
. 5 7
. . .
. . .
Sur la première ligne 70, on ajoute 2, puisque 2 * 5 * 7 = 70.
2 5 7
. . .
. . .
64 c’est 2^6, 4 (2^2) et 8 (2^3) figurent donc dans cette colonne, en compagnie du 2. 8 ne peut être sur la ligne de 108, car il y a tout au plus 2^2 dans cette ligne, mais 48 peut contenir 2^3 :
2 5 7
8 . .
4 . .
Restent à poser : 1, 3, 6 et 9.
Il manque 6 à la ligne 48, soit 1 et 6, et 9 à la colonne 45, soit 1 et 9, nous pouvons donc les poser d’une façon et unique ainsi que 3 pour terminer :
2 5 7
8 1 6
4 9 3
8h33
5e défi
Soient a et b les nombres recherchés. Alors :
ab+a+b=1+…+17= \(\frac {17×18}{2}\)=153
Ajoutons 1 puis factorisons :
ab+a+b+1=154
(a+1)(b+1)=2×7×11
L’un des facteurs du membre gauche, disons b+1, est le produit de 2 nombres parmi 2,7,11, mais comme b≤17, soit b+1≤18, la seule possibilité est b+1=2×7=14, d’où :
b=14−1=13
a=11−1=10.
9h01
5e défi
1+2+…+17−a−b=ab
153=ab+a+b
153=a.(b+1)+b
153=a.(b+1)+(b+1)−1
153=(a+1).(b+1)−1
154=(a+1).(b+1).
Et après, la rédaction est complète -)