
Premier défi : le problème du mois
Les mesures des côtés d’un triangle rectangle sont 60 cm, 80 cm et 100 cm. Déterminer la mesure du segment joignant le sommet de l’angle droit à l’hypoténuse et qui divise le triangle en deux triangles de même périmètre.


Solution du premier défi
Dans la figure ci-dessous, \(AB=60\,\mathrm{cm}\), \(AC=80\,\mathrm{cm}\), \(BC=100\,\mathrm{cm}\) et \(\widehat{BAC}=90^\circ\).
Si le triangle \(ABD\) a le même périmètre que le triangle \(ADC\), alors \(AB+BD\) doit être égal à \(AC+CD\), puisque les triangles ont en commun le côté \([AD]\).
Ainsi, on a
\(60+BD=80+(100-BD)\) et on obtient \(BD=60\,\mathrm{cm}\) et \(DC=40\,\mathrm{cm}\). On trace \([DE]\) perpendiculaire à \((AC)\) et on applique le théorème de Thalès.
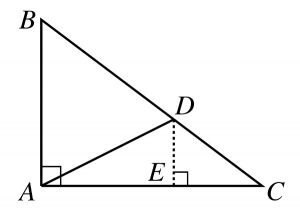
\[\frac{ED}{AB}=\frac{DC}{BC}=\frac{EC}{AC},~\text{ c’est-à-dire }~\frac{ED}{60}=\frac{40}{100}=\frac{EC}{80}.\]
On en déduit que \(ED=24\,\mathrm{cm}\) et \(EC=32\,\mathrm{cm}\).
On trouve ainsi \(AE=80-32=48\,\mathrm{cm}\) et, en appliquant le théorème de Pythagore dans le triangle \(AED\), on obtient \(AD=24\sqrt{5}\,\mathrm{cm}\).
Deuxième défi
Marc avait 84 timbres dans son album rouge et 20 dans son album bleu. Aujourd’hui, il a collé le même nombre de timbres dans chaque album. Si l’album rouge contient maintenant trois fois plus de timbres que l’album bleu, combien de timbres a-t-il collés dans chaque album ?


Solution du deuxième défi
On note x le nombre de timbres collés dans chaque album. On a alors
\[84+x=3×(20+x).\]
On résout cette équation et on obtient \(x=12\).
Marc a donc collé \(12\) timbres dans chaque album.
Troisième défi
Recouvrir le carré avec les formes

.
(et leurs rotations) de sorte que la somme des nombres contenus dans chaque forme soit toujours la même.

.


Solution du troisième défi
Il y a \(24\) cases, donc on va devoir utiliser huit formes. La somme de tous les nombres est égale à \(120\), donc la somme dans chaque forme doit être égale à \(15\). En raisonnant par exemple à partir des cases 8 du coin en haut à droite, on peut vérifier que la seule manière de couvrir le carré est la suivante :
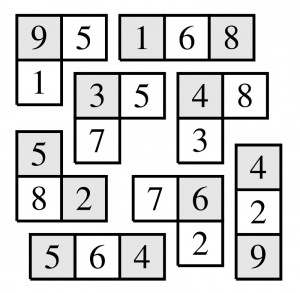
.
Quatrième défi
Charlie fait la somme de tous les entiers entre deux entiers \(a\) et \(b\), en comptant \(a\) et \(b\). Si \(1\leq a\leq 10\) et \(11\leq b\leq 20\), alors parmi les nombres \(91\), \(92\), \(95\), \(98\) et \(99\), lequel n’est pas une somme possible pour Charlie ?


Solution du quatrième défi
Il n’existe pas d’entiers \(a\) et \(b\) permettant d’obtenir une somme égale à \(98\).
On observe que :
\[1+2+\cdots +13=\frac{1}{2}\times14\times 13=7\times 13 = 91,\]
\[4+5+\cdots +14=99,\]
\[5+6+\cdots +14=95\]
\[\text{ et }8+9+\cdots +15=92.\]
Reste à prouver que \(98\) n’est pas une somme possible.
Supposons qu’il existe des entiers \(a\) et \(b\) avec \(1\leq a\leq 10\) et \(11\leq b\leq 20\), tels que \(98=a+(a+1)+\cdots + b\).
On a \(b=a+k\) pour un certain entier \(k\leq 19\).
Ainsi,
\[
\begin{eqnarray*}
98 & = & a+ (a+1)+\cdots + (a+k)\\
& = & (k+1)a + (1+2+\cdots +k)\\
& = & (k+1)a + \frac{1}{2}k(k+1)\\
& = & \frac{1}{2}(k+1)(2a+k).
\end{eqnarray*}
\]
On obtient donc \(196=(k+1)(2a+k)\). Puisque \(196=2^2\times 7^2\) et \(2\leq k+1\leq 20\),
les valeurs possibles pour \(k+1\) sont \(2\), \(4\), \(7\) ou \(14\). Si \(k+1=2\), alors
\(a=\frac{97}{2}\) n’est pas un nombre entier. Si \(k+1=4\), alors \(a=23>10\), ce qui contredit l’énoncé. De même, si \(k+1=7\), alors \(a=11>10\). Si \(k+1=14\), alors \(a=\frac{1}{2}\) n’est pas entier.
Finalement, il n’existe pas d’entiers \(a\) et \(b\) permettant d’obtenir une somme égale à \(98\).
Cinquième défi
Un avion met sept heures de plus qu’un autre pour aller de \(A\) à \(B\). Les vitesses de ces avions sont \(660\) km/h et \(275\) km/h. Quelle est la distance entre \(A\) et \(B\) ?


Solution du cinquième défi
La réponse est \(3300\) km.
Soit \(d\) la distance entre \(A\) et \(B\). On a alors
\[
\frac{d}{275}=\frac{d}{660}+7.
\]
D’où
\[
\begin{eqnarray*}
\frac{660d}{275}-d &=& 660\times 7\\
\frac{385d}{275} &=&4620\\
\frac{7d}{5} &=& 4620\\
d &=& \frac{5\times 4620}{7}= 3300\,\mathrm{km}.
\end{eqnarray*}
\]
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h28
1er défi
La moitié de l’aire du triangle rectangle est \(\frac{60 \times 80}{4} = 30 \times 40\). Ce triangle est partagé par le segment de longueur inconnue \(x\) en deux triangles, respectivement de bases \(60\) et \(80\), de hauteurs \(h_1\) et \(h_2\), et donc d’aires \(\frac{60 \times h_1}{2} = 30 h_1\) et \(\frac{80 \times h_2}{2} = 40 h_2\). Et ces aires sont égales à la moitié de celle du triangle rectangle, donc \(h_1 = 40\) et \(h_2 = 30\). Le segment de longueur \(x\) est aussi la diagonale d’un rectangle de côtés \(h_1\) et \(h_2\), donc \(x^2 = h_1^2 + h_2^2\), soit \(x=\sqrt{40^2+30^2}=50\).
8h39
Mais on veut le même périmètre, pas la même aire…
9h34
Bonjour, pour rester dans le hors-sujet, le fait que le milieu de l’hypoténuse (et centre du cercle circonscrit) permet de partager le triangle en deux triangles de même aire est assez évident sans calcul : les deux triangles ont des bases de même longueur (la moitié de l’hypoténuse) et une hauteur commune !
8h50
1er défi
Le segment (appelons le AD) issu du sommet de l’angle droit A est commun aux deux triangles : l’égalité des périmètres revient donc à 60+x=(100-x)+80, si je note ABD et ACD mes deux demi triangles, avec AB=60, AC=80, et x la distance BD
Soit x=60
9h06
1er défi
En égalant les 2 triangles, puis en appliquant Thalès et 2 fois Pythagore, on trouve :
X=√(24²+(80-32)²)=53,66
12h26
1er défi
Le triangle \(ABC\) est rectangle en \(B\).
La distance \(x\) est entre \(B\) et un point \(I\) de \(AC\).
On a \(AJ+80=(100-AJ)+60\).
Alors \(AJ=40\).
On mène une perpendiculaire à \((AB)\) qui passe par \(I\) et la coupe en \(K\).
On mène une perpendiculaire à \((AC)\) qui passe par \(I\) et la coupe en \(L\).
Puisque \((JK)//(CB)\), par une première thalesserie, on a : \(JK/40=60/100\) ou \(JK=24\).
Puisque \((JL)//(AB)\), par une deuxième thalesserie, on a : \(JL/60=80/100\) ou \(JL=48\).
Alors, par une pythagorerie, \(x^2=24^2+48^2\) ou \(x^2=5.24^2\) ou \(x=24\).\(\sqrt{5}\)
12h30
Deux erreurs : le \(J\) se transforme en \(I\) et inversement et une erreur : on mène une perpendiculaire à \((BC)\) qui passe par \(J\) et la coupe en \(L\).
12h32
Donc on a \(I=J\)…
10h25
2e défi
L’écart de 64 n’est pas modifié et devient le double du bleu. Marc a donc collé 64/2-20 = 12 timbres.
11h19
Non, 64/2-20 = 17
11h55
64/2=32 ; 32-20=12
Après avoir collé 12 timbres : bleu 32 ; rouge 84 + 12 = 96 = 3 x 32
10h24
J’aime beaucoup la manière de poser que l’écart n’est pas modifié : très joli 🙂 !!!
12h18
Mille excuses, j’ai fait le problème de tête et me suis mélangé dans mes calculs.
10h28
Oui oui on comprend bien que, de votre tête, 64/2=74/2=37 😉
12h44
3e défi
La somme de tous les nombres est 120. Comme il y a 5 * 5 – 1 = 24 cases, la somme des nombres dans chaque forme est : 120 / 24 * 3 = 15.
En étiquetant les lignes de A à E, de haut en bas, et les colonnes de 1 à 5, de gauche à droite, on pose de façon forcée :
A3, A4, A5 ; B4, B5, C4 ; B2, B3, C2 ; A1, A2, B1 ; C1, D1, D2 ; E1, E2, E3 ; D3, D4, E4 ; C5, D5, E5.
15h10
4e défi
La somme en question est la différence entre la somme des b premiers entiers et celle des a-1 premiers entiers.
C’est donc \(b(b+1)/2 – (a-1)a/2 = (1/2)(b^2-a^2+b+a) = (1/2)(b+a)(b-a+1)\)
Bien sûr, il est possible d’opérer les 10*10=100 calculs différents et observer celle des sommes proposées qui ne sort pas.
Mais, puisque dans la formule dernière apparaissent deux facteurs qui sont de parités différentes, la somme n’est paire que si b+a = 0 mod 4 ou si b-a+1 = 0 mod 4.
Risquons-nous à essayer de constater que c’est l’une des solutions paires qui n’est pas possible ; nous avons 3 chances sur 5 de perdre notre temps, et 2 sur 5 d’en gagner.
La première condition est équivalente à a et b pairs, ce qui peut conduire à 25 sommes.
La seconde est équivalente à b-a = 3 mod 4, ce qui peut conduire à 11 sommes (nombre établi ici par déroulement des possibilités).
Par la première condition, et une fois de plus par déroulement des possibilités, nous tombons sur la somme des entiers de 8 à 15 égale à 92.
Nous poursuivons par cette première condition, puis par la seconde, et nous ne tombons pas sur 98.
98 n’est pas une somme possible pour Charlie.
10h08
4e défi
\(91=7*13\)
\(92=2*2*23\)
\(95=5*19\)
\(98=2*7*7\)
\(99=3*3*11\)
Une de ces cinq valeurs n’est pas possible. C’est-à-dire que l’une des valeurs ne respecte pas une contrainte.
\(a+…+b=(1+2+…+(a-1)+a+…+b)-(1+2+…+(a-1))\) ou \(a+…+b=(b+1).b/2-(a).(a-1)/2\) ou encore \(a+…+b=(b+a).(b-a+1)/2\)
Quand l’un des facteurs est impair, l’autre est pair. Quand on divise celui des deux qui est pair par \(2\), il peut donner un résultat pair ou impair.
Quand la division donne un résultat impair, le produit est impair, sans que je vois de contrainte particulière donc rien n’empêche \(91\), \(95\) et \(99\) d’être des résultats de la somme \(a+…+b\).
Quand la division donne un résultat pair, le produit est pair avec pour contrainte que le facteur qui était pair devait donc rester pair après une division par \(2\) : le facteur pair devait donc être en plus un multiple de \(4\). Le résultat pair de la \(a+…+b\) doit être multiple de \(4\) : \(98=2*7*7\) ne convient pas.
15h08
4e défi
On a aussi :
\(a+b\) est compris entre \(11\) et \(30\).
\((b+a).(b-a+1)\) peut être égal à \(182=14*13\), à \(184=8*23\), à \(190=10*19\) et à \(198=18*11\) ou à \(198=9*22\).
Amusons-nous avec le dernier, \(198\).
On peut avoir \((b+a)=18\) et \((b-a+1)=11\) ce qui conduit à \(b=14\) et \(a=4\).
On peut avoir \((b+a)=11\) et \((b-a+1)=18\) ce qui conduit à \(b=14\) et \(a=-3\) ce qui n’est pas possible même si la somme des entiers relatifs entre \(-3\) et \(3\) est nulle.
On peut avoir \((b+a)=22\) et \((b-a+1)=9\) ce qui conduit à \(b=15\) et \(a=7\).
On peut avoir \((b+a)=9\) et \((b-a+1)=22\) ce qui conduit à \(b=15\) et \(a=-6\) ce qui n’est pas possible.
Et alors pour \(196=2*2*7*7\) la seule possibilité respectant la contrainte sur \(a+b\) est \((b+a)=14\) et \((b-a+1)=14\) ce qui conduit à \(2.b=27\) ce qui n’est pas possible puisque \(b\) est un entier.
C’est une autre raison pour laquelle \(98\) ne pourra pas être une somme.
L’avantage de cette méthode est qu’elle construit des valeurs de \(a\) et \(b\).
Et j’aime bien avoir montré que \(4+5+…+14=7+8+…+15=99\) soit qu’il existe plus de un couple \((a;b)\) pour une même valeur de somme.
15h14
Ah zut.
On a aussi \(b+a=28\) et \(b-a+1=7\) ce qui donne \(b=17\) et \(a=11\) qui ne respecte pas la contrainte sur \(a\) mais qui donne bel et bien \(11+12+…+17=98\).
Je ne comprends plus la pertinence de mon argument en termes de multiple de \(4\) des sommes paires…
15h57
4e défi
C’est le produit \((b-a+1)(b+a)\) qui doit être multiple de \(4\) quand sa moitié, la somme de Charlie, est paire. Mais la somme elle-même peut très bien être paire sans être multiple de \(4\). Par exemple avec \(a=9\) et \(b=11\), on a \(9+10+11 = 30 = 2 \times 15\).
16h30
4e défi
Tout entier supérieur à 6 produit d’un entier pair et d’un entier impair est égal à une somme d’entiers consécutifs ?
9h12
Soit \(N=a+…+b\) la somme de tous les entiers compris entre \(a\) et \(b\), \(a\) et \(b\) compris.
Si \(N=(2q).(2.p+1)=a+…+b=((b+a).(b-a+1)/2\) alors
\(b=2.q+p\)
\(a=2.q-p\)
17h33
4e défi
Notons \(C(a,b) = a+ … +b\) la somme de Charlie. Alors \(C(a,b) = \frac{(b-a+1)(b+a)}{2}\).
De \(1 \leq a \leq 10\) et \(11 \leq b \leq 20\), on tire \(2 \leq b-a+1 30\), trop grand.
avec \(i=19\) on obtient \(p=10\) puis \(95=C(5,14)\)
Pour \(98=2 \times 7^2\) on n’a aucune solution :
avec \(i=7\) on obtient \(p=28\), puis \(a=11>10\), trop grand.
Pour \(99=3^2 \times 11\) on a \(2\) solutions :
avec \(i=3\) on obtient \(p=66 > 30\), trop grand.
avec \(i=9\) on obtient \(p=22\) puis \(99=C(7,15)\)
avec \(i=11\) on obtient \(p=18\) puis \(99=C(4,14)\)
L’intrus est donc \(98\).
20h28
4e défi
Le sujet indique qu’il n’y a qu’un intrus, or 98 est le seul divisible par un carré. (soupçon)
On a alors (a+b)(b-a+1) = 4×7².
On sait qu’ils ne sont pas de même parité , que (a+b)>(b-a+1) (différence 2a-1) et qu’aucun n’est divisible par 49 donc on ne peut qu’avoir a+b = 28 et b-a+1 = 7 ce qui a = 11 et b =17 : impossible.
Pour être complète 2a-1 n’est négative que si a = 0 mais alors b(b+1) = 2²X7² or ce nombre n’a pas 2 diviseurs consécutifs (sauf 1 et 2).
13h55
4e défi
La somme des nombres de \(\,a\,\) à \(\,b\,\) est \(\,S(b, a)= \frac{b(b+1)}{2}-\frac{a(a-1)}{2} \)
On sait que \(\,1\leq a \leq 10\,\) donc \(\,0\leq \frac{a(a-1)}{2}\leq 45\)
Et puisque \(\,91\leq \frac{b(b+1)}{2}-\frac{a(a-1)}{2} \leq 99\,\), on a \(\,91 \leq \frac{b(b+1)}{2}\leq 144\,\) d’où \(\,13\leq b \leq 16\)
Si \(\,b=13\,\) alors \(\,91\leq 91-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,-8 \leq \frac{a(a-1)}{2} \leq 0\,\) et \(\,a=1\,\)
Si \(\,b=14\,\) alors \(\,91\leq 105-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,6 \leq \frac{a(a-1)}{2} \leq 14\,\) et \(\,a=4\,\) ou \(\,5\,\)
Si \(\,b=15\,\) alors \(\,91\leq 120-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,21 \leq \frac{a(a-1)}{2} \leq 29\,\) et \(\,a=7\,\) ou \(\,8\,\)
Si \(\,b=16\,\) alors \(\,91\leq 136-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,37 \leq \frac{a(a-1)}{2} \leq 45\,\) et \(\,a=10\,\)
Les sommes possibles sont alors :
\(\,S(13, 1)=91-0=91\, \hspace{2cm}S(14, 4)=105-6=99\, \hspace{2cm}S(14, 5)=105-10=95\,\)
\( \,S(15, 7)=120-21=99 \hspace{1.5cm} S(15, 8)=120-28=92 \hspace{1.8cm} S(16, 10)=136-45=91\, \)
La somme obtenue par Charlie ne peut donc pas être égale à \(98\).
8h56
5e défi
Supposons que les avions partent en même temps de \(A\) en direction de \(B\) mais ne s’arrêtent pas en \(B\). Alors la distance entre les avions est proportionnelle au temps de vol. Au bout d’une heure elle est de \(660-275=385\) km, et quand l’avion lent arrive en \(B\), l’autre a parcouru \(7 \times 660 = 4620\) km de plus que lui. Donc le temps de vol de l’avion lent entre \(A\) et \(B\) est de \(\frac{4620}{385} = 12\) heures, pendant lesquelles il a parcouru \(12 \times 275 = 3300\) km.
15h11
5e défi
Soit \(t\) le temps (en h) mis par l’avion le plus rapide pour parcourir la distance \(AB\).
La vitesse et le temps des deux avions permet d’exprimer la distance \(AB\) (en km) de deux façons en fonction de \(t\). On a \(AB=\,660\,t\,\) et \(AB=\,275\left(t+7\right)\,\).
Or, \(\,660\,t=275\left(t+7\right)\,\Leftrightarrow\,12t=5(t+7) \,\Leftrightarrow\, 12t=5t+35 \,\Leftrightarrow\, 7t=35 \,\Leftrightarrow\, t=5\,\).
On a donc \(AB=660\times5=3300\,\) km.