
Premier défi
Si le carré fait \(1\,\textrm{m}\) de côté, quelle est l’aire de la région coloriée ?
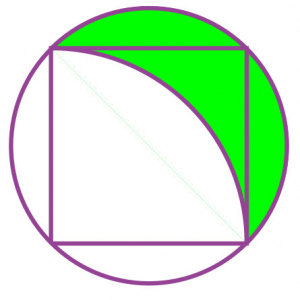
.


Solution du premier défi
\(\displaystyle\frac\pi 4 – \frac 12 +1-\frac{\pi}{4}=\frac{1}{2}\,\textrm{m}^2.\)
On remarque que le rayon du cercle est la moitié de la diagonale du carré inscrit. D’après le théorème de Pythagore, la diagonale du carré mesure \(\sqrt 2\,\textrm{m}\), ainsi le cercle a un rayon de \(\frac{\sqrt 2}{2}\,\textrm{m}\).
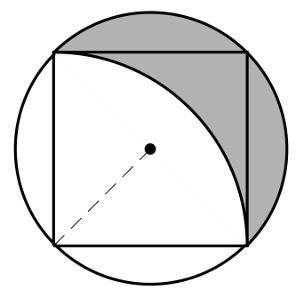
image 1
L’aire du disque correspondant est donc \(\pi\left(\frac{\sqrt 2}{2}\right)^2=\frac{\pi}{2}\,\textrm{m}^2\). L’aire du carré valant \(1\,\textrm{m}^2\), on en déduit que l’aire des deux régions coloriées extérieures au carré est \(\frac{\frac{\pi}{2}-1}{2}= \frac\pi 4 – \frac 12\,\textrm{m}^2\).
Il nous reste à calculer l’aire de la région coloriée intérieure au carré. On remarque que cette aire est égale à l’aire du carré moins le quart de l’aire du disque délimité par les pointillés, c’est-à-dire \(1-\frac{\pi}{4}\,\textrm{m}^2\).
image 2
Donc l’aire de la région coloriée est
\(\displaystyle\frac\pi 4 – \frac 12 +1-\frac{\pi}{4}=\frac{1}{2}\,\textrm{m}^2.\)
Deuxième défi
Une voiture, un camion, un bus et une moto roulent à vitesse constante. La voiture dépasse le camion à 10h, puis dépasse le bus à midi et enfin la moto à 14h. À 16h, le bus dépasse la moto et le camion rattrape le bus à 18h. Si la voiture et le bus roulent respectivement à 120km/h et 80km/h, quelles sont les vitesses du camion et de la moto ?


Solution du deuxième défi
Réponse :
\(\frac{720}{8}=90\,\textrm{km/h}\).
Notons \(A\) le point où se situent la voiture et le bus à midi, \(B\) le point où se situent la voiture et la moto à \(14\,\textrm{h}\) et \(C\) le point où se situent le bus et la moto à \(16\,\textrm{h}\).
Entre \(14\,\textrm{h}\) et \(16\,\textrm{h}\), la moto a parcouru la distance \(BC\). Or \(BC=AC-AB\).
Comme \(AC\) est la distance parcourue par le bus en \(4\) heures et que le bus roule à \(80\,\textrm{km/h}\), on a \(AC=4 \times 80=320\,\textrm{km}\).
De même, comme \(AB\) est la distance parcourue par la voiture en \(2\) heures et que la voiture roule à \(120\,\textrm{km/h}\), on a \(AB= 2 \times 120=240\,\textrm{km}\).
Donc la moto a parcouru en \(2\) heures la distance \(BC=320-240=80\,\textrm{km}\). Elle roule donc à \(40\,\textrm{km/h}\).
Notons \(D\) le point où se situent la voiture et le camion à \(10\,\textrm{h}\) et \(E\) le point où se situent le bus et le camion à \(18\,\textrm{h}\).
\(DA\) est la distance parcourue par la voiture en \(2\) heures soit \(240\,\textrm{km}\), \(AE\) est la distance parcourue par le bus en \(6\) heures soit \(6 \times 80=480\,\textrm{km}\).
Le camion a donc parcouru en \(8\) heures la distance \(DE=DA+AE=240+480=720\,\textrm{km}\). La vitesse du camion est donc \(\frac{720}{8}=90\,\textrm{km/h}\).
Troisième défi
Lorsque le chameau a soif, \(84\,\%\) de son poids est de l’eau. Après avoir bu tout ce qu’il peut, son poids atteint \(800\,\textrm{kg}\) et l’eau représente alors \(85\,\%\) de son poids. Combien pèse le chameau lorsqu’il a soif?


Solution du troisième défi
Réponse : \(750\,\textrm{kg}\)
Quand le chameau boit tout ce qu’il peut, \(15\,\%\) de ses \(800\,\textrm{kg}\) ne sont pas de l’eau, ce qui représente \(800\times 0{,}15=120\,\textrm{kg}\).
Ces \(120\,\textrm{kg}\) sont \(16\,\%\) de son poids lorsqu’il a soif.
Par conséquent, le chameau pèse, lorsqu’il a soif, \(120\times \frac{100}{16}=750\,\textrm{kg}\).
Quatrième défi
Soit \(N=n^2\) un carré parfait constitué de quatre chiffres, tous strictement inférieurs à \(7\). Si l’on ajoute \(3\) à chaque chiffre de \(N\), on obtient un autre carré parfait. Trouver \(n\).


Solution du quatrième défi
Réponse : \(n=34\)
Nous savons que \(N+3333=n^2+3333\) est un carré parfait.
Posons \(M=m^2=n^2+3333\).
On a alors \(M-N=m^2-n^2=(m+n)(m-n) = 3333=3\times 11\times 101\).
Les valeurs possibles du couple \((m+n,m-n)\) sont donc \((3333,1)\), \((1111, 3)\), \((303,11)\) et \((101,33)\).
Or \(m^2\) ne contient que \(4\) chiffres, donc \(n<m<100\).
L’unique possibilité est donc \(m+n=101\) et \(m-n=33\), donc \(m=67\) et \(n=34\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h43
1er défi
L’aire de la lunule recherchée est la somme d’un demi disque de diamètre \(\sqrt{2}\) et la moitié d’un carré de côté 1 moins la surface d’un quart de disque de côté \(1\). Donc son aire est :
\(\frac{1}{2}\times\left(\frac{\sqrt{2}}{2}\right)^2\pi+\frac{1}{2}-\frac{1}{4}\times1^2\pi\)
8h46
Soit une aire égale à \(\frac{\pi}{4}+\frac{1}{2}-\frac{\pi}{4}=\frac{1}{2}\)
8h49
1er défi
Le diamètre du grand disque est la diagonale du carré donc de longueur \(\sqrt{2}\). L’aire du grand disque est donc \(\pi(\frac{\sqrt{2}}{2})^2=\frac{\pi}{2}\). La moitié de cette surface est verte sauf une zone qui est la différence entre la partie blanche du carré et la moitié du carré.
La partie blanche du carré est un quart de disque de rayon \(1\) donc son aire est \(\frac{\pi}{4}\), et le carré a une aire totale de \(1\).
L’aire totale de la région verte est donc \(\frac{\pi}{4}-(\frac{\pi}{4} – \frac{1}{2})=\frac{1}{2}\).
9h18
2e défi
Dans le référentiel du bus, la voiture roule à \(120-80=40\) km/h, donc elle parcourt \(80\)km entre ses rencontres avec le camion à \(10\)h et le bus à \(12\)h. Le camion met \(18-10=8\)h à parcourir ces \(80\)km par rapport au bus donc sa vitesse relative est \(80/8=10\)km/h et sa vitesse par rapport au sol est \(80+10=90\)km/h.
La rencontre entre la voiture et la moto (\(14\)h) a lieu exactement au milieu de l’intervalle séparant leurs rencontres respectives avec le bus (\(12\)h et \(16\)h), donc la vitesse de la moto (qui recule par rapport au bus) est l’opposée de celle de la voiture dans le référentiel du bus, soit \(-40\)km/h. Sa vitesse par rapport au sol est donc \(80-40=40\)km/h.
15h48
2e défi
Considérons trois véhicules \(A\), \(B\) et \(C\) roulant chacun à une vitesse constante (resp. \(v_A\), \(v_B\) et \(v_C\) en km/h) et amenés à se doubler. Notons \(M_1\) l’instant où \(A\) double \(C\), \(M_2\) l’instant où \(A\) double \(B\) et \(M_3\) l’instant où \(C\) rattrape \(B\).
Alors la distance parcourue par \(C\) entre \(M_1\) et \(M_3\) est égale à la somme des distances parcourues par \(A\) entre \(M_1\) et \(M_2\) et par \(B\) entre \(M_2\) et \(M_3\).
On a donc : \((t_1+t_2)\times v_C =t_1\times v_A+t_2 \times v_B\:\:\:\) soit \(\:\:\:v_C = \frac{t_1\times v_A+t_2 \times v_B}{t_1+t_2}\)
\(\phantom{espace}\)
Si \(A\) interprète la voiture, \(B\) le bus et \(C\) le camion, alors la vitesse du camion devient :
\(\phantom{espace}\)
\(v_C=\frac{2\times120+6\times80}{8}=\frac{240+480}{8}=\frac{720}{8}=90\) km/h
\(\phantom{espace}\)
Si \(A\) interprète la voiture, \(B\) la moto et \(C\) le bus, on obtient :
\(\phantom{espace}\)
\(4\times 80=2\times 120+2\times v_B\:\:\:\) d’où \(\:\:\:v_B=\frac{4\times 80-2\times 120}{2}=\frac{320-240}{2}=\frac{80}{2}=40\) km/h
Le camion roule donc à \(90\) km/h et la moto à \(40\) km/h
15h51
Kamakor
Note : \(t_1\) est la durée entre les instants \(M_1\) et \(M_2\) et \(t_2\) la durée entre les instants \(M_2\) et \(M_3\)
16h27
2e défi
Le camion roule de 10h à 18h, soit 8h. Pendant ce temps il parcourt les 240km de la voiture (2h x 120km/h) + les 480km du bus (6h x 80km/h) soit au total 720km.
V. du camion : 720/8= 90km/h
La moto roule de 14h à 16h soit 2h. Pendant ce temps elle parcourt les 320km du bus (4h x 80km/h) – Les 240km de la voiture ( 2h x 120km/h) soit au total 80km
V. de la moto : 80/2= 40km/h
7h48
3e défi
Soit p le poids du chameau avant de boire.
L’eau bue= 800-p
La masse d’eau contenue dans le chameau,quand il a bu
= 0,85×800
Cette masse d’eau est aussi égale à la masse d’eau contenue dans le chameau avant de boire, soit 0,84p, plus l’eau qu’il a bu soit 800-p
On a donc :
0,85×800=0,84p+800-p
Soit p=800(0,15/0,16)
p=750kg
8h26
3e défi
Si l’eau représente \(85\) % des \(800\) kg, le chameau complètement déshydraté pèse \(0,15\times800=120\) kg. Ce qui correspond à \(100-84=16\) % de la masse du chameau avant qu’il ait bu. Le chameau assoiffé pèse donc \(120\div 0,16=750\) kg
18h02
3e défi
Allez bossons une fois :
Un chameau lyophilisé pèse (100%-84%)=16% de son poids P lorsqu’il est déshydraté (assoiffé).
Ce même chameau lyophilisé pèse (100%-85%) 800 kg pour le cas où il est hydraté.
=> Donc hydraté ou pas, un chameau lyophilisé pèse P = (15% 800 kg) / 16% = 15*50 kg =750 kg
Conclusion : Cela fait lourd pour un sachet de chameau en poudre 🙂
7h55
4e défi
On a n^2 + 3333 = a^2
soit a^2 – n^2 = 33 x 101
d’où (a-n)(a+n) = 33 x 101
ou encore a-n=33 et a+n = 101 qui donnent a = 67 et n=34
11h27
4e défi
1000 n=34
12h27
Oui, et pour être tout à fait complet, il y a aussi \((p-n)(p+n) = 11 \times 303\) qui ne convient pas.
11h10
Même si \(24649−21316=3333 \)😉