
Premier défi
Annie possède un récipient de \(10\) litres de jus. Elle a également deux autres récipients, vides, de capacités \(3\) et \(7\) litres. En utilisant uniquement ces trois récipients, Annie peut-elle partager en deux parts égales les \(10\) litres de jus ?


Solution du premier défi
Réponse : oui.
En suivant les étapes indiquées dans le tableau suivant, Annie peut partager les dix litres de jus en deux parts égales.
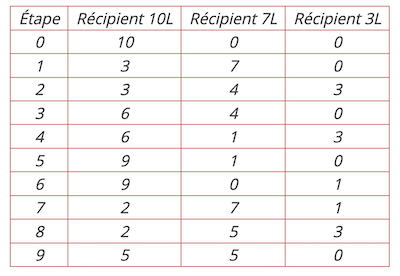
.
Deuxième défi
Xavier a trouvé une carte au trésor. À partir d’un arbre, il doit marcher : \(35\) pas vers l’est; \(30\) pas vers le nord; \(15\) pas vers l’ouest; \(10\) pas vers le nord; \(60\) pas vers l’est; \(20\) pas vers le nord. À quelle distance de l’arbre se trouve le trésor ?


Solution du deuxième défi
Réponse : \(100\) pas.
En prenant l’arbre comme origine et \(10\) pas comme unité de longueur du plan cartésien (un arbre ne pouvant se trouver trop proche d’un pôle, l’approximation plane cartésienne semble raisonnable), on obtient la figure suivante~:
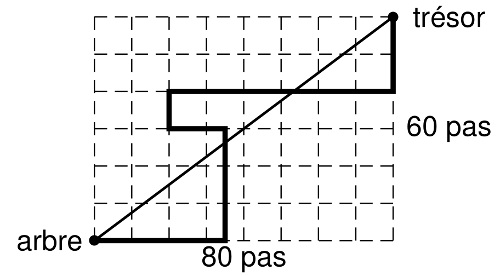
.
Ainsi, il faut marcher \(35-15+60=80\) pas vers l’est et \(30+10+20=60\) pas vers le nord.
D’après le théorème de Pythagore, la distance entre l’arbre et le trésor est de
\[\sqrt{60^2+80^2}=\sqrt{10\,000}=100\, \, \text{pas} \].
Troisième défi
Carmen se sert une tasse de café, en boit la moitié et se rend compte qu’il est trop fort. Elle remplit alors la tasse de lait et mélange. Elle boit alors un quart de tasse et, trouvant que, décidément, le café est toujours trop fort, complète ce qui reste avec du lait. Quelle proportion de café reste-t-il dans la tasse ?


Solution du troisième défi
Réponse : \(\frac{3}{8}\) de tasse de café et le reste est du lait.
Le premier remplissage avec du lait donne un mélange composé pour moitié de café.
Après avoir bu le quart de tasse, la moitié des \(\frac{3}{4}\) de tasse restants est du café.
Donc, à la fin, il y a \(\frac{3}{8}\) de tasse de café et le reste est du lait..
Quatrième défi
L’opération suivante est incorrecte. En déplaçant seulement deux allumettes, comment la corriger ?



Solution du quatrième défi
Une possibilité est
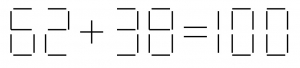
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h37
1er défi
10, 7, 7, 4, 4, 1, 1, 8, 8, 5, 5
0, 0, 3, 3, 6, 6, 7, 0, 2, 2, 5
0, 3, 0, 3, 0, 3, 2, 2, 0, 3, 0
10h47
Je ne vois pas comment vous passez de \(\begin {Bmatrix}1\\6\\3\end{Bmatrix}\) à \(\begin {Bmatrix}1\\7\\2\end{Bmatrix}\) A priori on ne peut pas extraire seulement 1 litre du récipient plein de 3 litres.
9h27
1er défi
Bruce Willis et Samuel L. Jackson le font à la perfection dans Die Hard 3 🙂
12h34
1er défi
Il y a 6l dans le récipient (contenance 7l).
On peut donc encore ajouter 1l dans ce récipient qu’on prélève du récipient de contenance 3l
17h56
Comme ça OK !
14h41
1er défi
On peut faire en 9 transvasements (solution optimale en parcourant le graphe des cas possibles) :
10 – 0 – 0
3 – 7 – 0
3- 4 – 3
6 – 4 – 0
6 -1 – 3
9 – 1 – 0
9 – 0 – 1
2 – 7 – 1
2 – 5 – 3
5 – 5 – 0
23h47
1er défi
Je n’arrive pas à voir où sont les maths dans ce jeu.
19h44
Pour voir où sont les maths dans cette énigme de transvasements, je vous conseille d’aller voir cette page http://villemin.gerard.free.fr/aJeux1/Mesure/Transvas.htm
7h34
2e défi
Si l’on place le parcours dans un repère orthonormé d’origine 0 ;0 le point d’arrivée a pour coordonnées 80,60.
La distance est donc : √80²+60²=100
9h23
3e défi
Bonjour
Soit x le volume du café.
Après avoir vidé la moitié de la tasse, il reste x/2 de café.
En prenant 1/4 du mélange café-lait, elle prend donc X/2 * 1/4 de café.
Il reste alors en café x/2 – x/8 soit 3x/8.
Il reste 3 huitièmes de café.
18h59
3e défi
Images des mathématiques se sont prises d’une passion pour les problèmes de dilutions chers aux chimistes : défis des 25/08, 08/09 et aujourd’hui, 20/10.
Alors un nouveau.
On admet que l’hydrolyse d’un peu de foie et de cœur de canard (\(50g\)) dans de l’eau conduit à une solution SMe de \(1L\) avec \(50g\) d’espèces chimiques dedans.
On dilue \(100\) fois SMe en obtenant \(1L\) d’une nouvelle solution SFi1.
On dilue ensuite \(100\) fois SFi1 en obtenant\(1L\) d’une nouvelle solution SFi2.
On dilue ensuite \(100\) fois SFi2 en obtenant\(1L\) d’une nouvelle solution SFi3.
Et ainsi de suite.
A partir de combien de dilution ne restera-t-il plus que la masse d’un atome d’hydrogène (\(0,00 000 000 000 000 000 000 000 000167kg\)) dans la solution ?
Remarque : ce protocole est appliqué \(200\) fois de suite afin d’obtenir un célèbre antigrippal faisant osciller en latin un coccyx ; montrer qu’à partir d’un certain rang, on dilue de l’eau dans de l’eau…
10h47
4e défi
On enlève une allumette verticale du premier \(8\) pour en faire un \(6\), et on la pose sur le \(-\) pour en faire un \(+\).

On décale une allumette verticale du second \(2\) vers la droite pour en faire un \(3\).