
Premier défi : le problème du mois
Dans la figure ci-dessous, un grand carré est découpé en deux rectangles et un petit carré rouge. Les aires des deux rectangles sont \(10\,cm^2\) et \(3\,cm^2\). Quelle est l’aire du petit carré rouge ?

.


Solution du premier défi
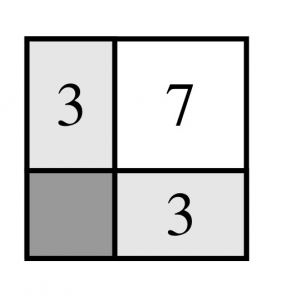
On découpe dans la figure un nouveau rectangle de \(3\) cm\(^2\) comme ci-dessous.
Solution
Par symétrie, le rectangle qui reste en haut à droite est en fait un carré et a pour surface \(10-3=7\) cm\(^2\). Son côté a donc pour longueur \(\sqrt{7}\,\)cm. Les rectangles de surface \(3\) cm\(^2\) ont donc un petit côté de longueur \(3/\sqrt{7}\). Comme c’est aussi le côté du petit carré, celui-ci a pour surface \(\frac 97{\rm cm}^2\)
Deuxième défi
Un tonneau est rempli d’eau. On vide la moitié de l’eau qu’il contient puis on ajoute un litre d’eau. Après avoir répété ces deux opérations cinq fois de suite, il reste trois litres d’eau dans le tonneau.
Quelle est la contenance du tonneau ?


Solution du deuxième défi
L’opération que l’on répète cinq fois consiste, s’il y a un volume \(V\) d’eau dans le tonneau, à en vider la moitié puis à rajouter un litre. À la fin de l’opération, il reste donc \(1+V/2\) litres.
En répétant deux fois l’opération, il reste \(1+(1+V/2)/2=1+1/2+V/4\) litres. Aux étapes suivantes, il reste donc \(1+(1+1/2+V/4)/2=1+1/2+1/4+V/8\), puis \(1+1/2+1/4+1/8+V/16\) et enfin \(1+1/2+1/4+1/8+1/16+V/32 = 1+15/16+V/32=3\).
On en déduit que \(V=32\times\frac{17}{16} = 34\).
Troisième défi
Soient \([PA]\), \([PB]\) et \([QR]\) trois segments tangents à un cercle comme ci-dessous.
Sachant que \(PA=5\,\)cm, combien mesure le périmètre du triangle \(PQR\) ?
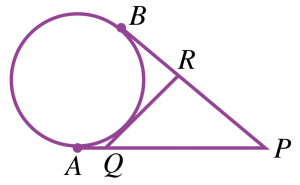
Figure du défi


Solution du troisième défi
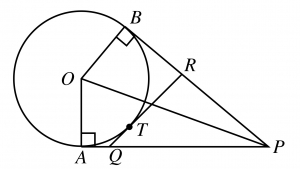
On note \(O\) le centre du cercle et \(T\) le point de contact du segment \([QR]\) avec le cercle.
La propriété de tangence montre que les triangles \(OAP\) et \(OBP\) sont rectangles. Comme ils ont deux côtés égaux, ils sont symétriques et \(PA=PB\).
solution du défi
Pour la même raison, on a \(QT=QA\) et \(RT=RB\).
On en déduit que le périmètre de \(PQR\) vaut
\begin{align*}
PQ+QR+RP
&= PQ+(QT+TR)+RP \\
&= (PQ+QA )+ (BR+RP)\\
&= PA+BP=2PA \\
&= 10\,\mathrm{cm}.
\end{align*}
Quatrième défi
Combien de nombres premiers peuvent s’écrire de deux manières distinctes comme la somme de deux autres nombres premiers ? L’ordre dans l’addition n’est pas pris en compte, autrement dit \(2+3\) et \(3+2\) ne comptent pas comme deux sommes distinctes.


Solution du quatrième défi
Le nombre premier \(2\) ne peut pas s’écrire comme la somme de deux nombres premiers. Soit donc \(p\) un nombre premier supérieur à \(3\). Il est forcément impair. S’il s’écrit comme somme de deux nombres premiers, l’un des deux doit donc être pair, donc égal à \(2\) et le second est alors forcément égal à \(p-2\). Il n’y a donc qu’une façon de l’écrire comme somme de deux nombres premiers. Il n’y a donc aucun nombre premier qui puisse s’écrire de deux manières distinctes comme somme de nombres premiers.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


14h06
1er défi
Appelons ‘x’ le petit côté du carré rouge. Puisque la figure constitue elle-même un carré, alors la longueur du rectangle d’aire 3 cm² est égale à la largeur du rectangle d’aire 10 cm². Appelons là ‘a’.
Nous constatons que :
ax = 3 cm²
a * (a + x) = 10; a² + ax = 10 cm²
En remplaçant ‘ax’ par 3, nous obtenons alors :
a² + 3 = 10; a² = 7; a = √7 cm
En remplaçant ‘a’ par la nouvelle mesure obtenue dans la première équation, nous calculons :
x√7 = 3; x = 3 / √7 cm
L’aire du petit carré rouge est donc :
(3 / √7)² = 9 / 7 cm².
17h16
En constatant que le rectangle de 10 cm² à qui on ote un rectangle de 3 cm² donne un carré de 7 cm², donc de côté √7 cm.
1ere solution: le rectangle de 3 cm² = x √7 , d’où x = 3/√7 ce qui donne l’aire du petit carré: 9/7.
2e solution: Soit un rectangle de côté a+b et x+y qu’on coupe en 4 rectangles de côté ax, ay, bx, by avec bien sûr aucun côté nul . On a l’égalité (ax)/(ay)=(bx)/(by). En appliquant cela à notre problème, cela donne S/3=3/7 d’où la surface du carré 9/7
Cette 2e solution je l’ai « trouvée » en constatant que 9/7=3*3/7 qui sont les surfaces de l’énigme 🙂
12h04
2e défi
En partant du résultat final et en procédant à l’envers, c’est à dire en soustrayant 1 et en multipliant par 2 et en répétant cette opération cinq fois on obtient successivement : 4, 6, 10, 18 et 34.
La contenance du tonneau est donc 34 litres.
22h42
Donc notre dernier enfant à ma femme et moi-même est en terminale et commence les suites dans la spé’ math’.
L’énoncé est donc clairement \( u_{n}=1/2.u_{n-1}+1 \).
22h44
\( u_{n-1}=1/2. u_{n-2}+1\) qui conduit à \( u_{n}=1/2^2. u_{n-2}+1/2+1\).
22h50
Une troisième ligne que je n’écris fait apparaitre \( u_{n}=1/2^n.(u_{0}-2)+2\).
Quand on inverse cette formule, on obtient \( u_{0}=2^n.(u_{n}-2)+2\).
Ici, \( n=5\) et \( u_{5}=3\) alors évidemment \( u_{0}=2^5.(3-2)+2=34\).
22h54
Si il reste \( 2\) litres, le tonneau contient \( 2\) litres 🙂
16h06
En bref, si \( u_0>2\) le tonneau se vide pour atteindre la valeur limite de \(2\) litres. Si \( u_0<2\) le tonneau se remplit pour atteindre la valeur limite de \(2\) litres et si \( u_0=2\) le tonneau reste toujours à \(2\) litres.
10h20
Ah, effectivement!
Joli!
12h35
3e défi
La position des points Q et R n’est pas précisée, donc le périmètre du triangle PQR est indépendant de la position des points Q et R.
Dans le cas limite où le point Q est confondu avec le point A et le point R avec le point P, le périmètre est égal à 2 fois AP.
Le périmètre du triangle PQR est donc 10 cm.
13h40
En notant \(C\) le point de contact du cercle avec la droite \((QR)\), on a \(QA= QC\) et \(RC=RB\). De plus \(PA=PB\)
Donc \(PR+PQ+QR=PR+PQ+QC+CR=PR+RB+PQ+QA= PA+PB = 10 cm \).
Le périmètre du triangle \(PQR\) ne dépend pas de la position des points \(Q\) et \(R\) et vaut \(10 cm\).
18h20
Je trace \(O\) le centre du cercle et \(H\) le point auquel la droite \((QR)\) est tangente au cercle.
\(OB=OH\) et comme \(OR\) est commun aux deux triangles \(OBR\) et \(OHR\) alors \(BR=RH\).
On montre de la même manière que \(AQ=QH\) dans les triangles \(OAQ\) et \(OQH\) et on montre de la même manière que \(BP=AP\) dans les triangles \(OBP\) et \(OAP\) ou on montre donc que \(BP=5cm\).
Le périmètre du triangle \(QRP\) est égal à \(QH+HR+RP+PQ\) ou encore \(AQ+BR+RP+PQ\) ou encore \(AP+BP\) soit \(5cm+5cm=10cm\).
15h27
Réflexe d’un ancien prof pointilleux. Dans votre preuve du fait que \( BR= RH\) il eût fallu signaler que les triangles \(OBR\) et \(OHR\) sont rectangles. Pour montrer que deux triangles sont isométriques il faut trois égalités. Souvenir de ma jeunesse avec » les cas d’égalité des triangles ».
15h22
4e défi
Bonjour,
Un nombre premier est soit impair, soit égal à 2.
La somme de deux nombres impairs est un nombre pair et donc n’est pas premier. Par conséquent l’un des deux nombres à additionner est obligatoirement 2. Il faudrait donc trouver deux nombres premiers différents a et b tels que 2+a = 2+b, ce qui est manifestement impossible.
La réponse à la question est donc 0