
Premier défi : le problème du mois
En écrivant bout à bout l’âge de Marie puis celui de Bruno, on obtient un nombre à quatre chiffres qui a la particularité d’être un carré parfait.
Dans \(31\) ans, si l’on écrit à nouveau leurs âges bout à bout, on obtiendra également un nombre à quatre chiffres et ce nombre sera, là encore, un carré parfait.
Déterminer les âges de Marie et Bruno.


Solution du premier défi
Réponse : Marie a 12 ans et Bruno a 25 ans.
Montrons d’abord que les âges de Marie et Bruno sont des nombres à deux chiffres.
Si jamais l’un des deux avait \(9\) ans ou moins, l’autre devrait alors avoir au moins \(100\) ans. Mais alors, dans \(31\) ans, leurs âges mis bout à bout formeraient un nombre à cinq chiffres, ce qui est exclu.
Notons donc \(ab= 10a+b\) (respectivement \(cd = 10c+d\)) l’âge de Marie (respectivement Bruno), où \(a, b, c\) et \(d\) sont des entiers entre \(0\) et \(9\).
On sait que le nombre à quatre chiffres \(abcd = 1000a+100b+10c+d\) est le carré d’un entier \(x\).
Dans \(31\) ans, leurs âges seront
\(10a+b+31 = 10(a+3)+(b+1)\) et \(10c+d+31 = 10(c+3)+d+1\).
Ce sont encore des nombres à deux chiffres et l’on sait que
\(1000(a+3)+100(b+1)+10(c+3)+d+1\) est le carré d’un autre entier \(y\).
On en déduit que
\begin{align*}
y^2 &= 1000(a+3)+100(b+1)+10(c+3)+d+1\\
&=abcd+3131 =x^2+3131,
\end{align*}
autrement dit \[(y-x)(y+x)=3131=31\times 101.\]
Comme \(y>x\), on a \(y-x=31\) et \(y+x=101\).
En résolvant ce système linéaire, on trouve \(x=35\) et \(y=66\).
Par conséquent, \(x^2=1225\) et \(y^2=4356\).
On en déduit que Marie a \(12\) ans et Bruno a \(25\) ans.
Deuxième défi
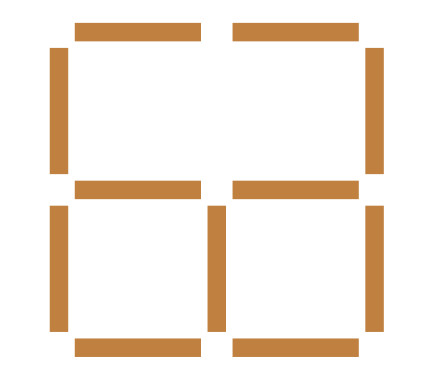
Sur la figure ci-dessous formée par des bâtonnets, on peut distinguer trois carrés : un grand et deux petits.
Déplacer quatre bâtonnets de sorte que la figure contienne alors quatre carrés de même taille.
.


Solution du deuxième défi

Troisième défi
Rebecca choisit trois nombres entiers positifs.
Elle confie à Iris que leur produit est égal à \(36\) et lui précise également leur somme.
Même avec ces deux informations, Iris ne peut toujours pas deviner quels sont ces trois nombres.
Que vaut la somme des trois nombres ?


Solution du troisième défi
Réponse : la somme est égale à \(13\).
Considérons les triplets ordonnés de trois nombres entiers positifs dont le produit vaut \(36\). Ces triplets sont les suivants :
\begin{align*}
(1, 1, 36), \ \ (1, 2, 18), ~ & ~ (1, 3, 12), \ \ (1, 4, 9), \\
(1, 6, 6),~ \ \ (2, 2, 9), ~ & ~ (2, 3, 6), ~ \ \ (3, 3, 4).
\end{align*}
Les sommes des composantes de ces triplets sont toutes différentes, à l’exception de \(1+6+6=13=2+2+9\).
Comme Iris est dans l’incapacité de deviner les trois nombres, cela signifie que la somme est égale à \(13\).
Quatrième défi
Dans la multiplication suivante, chacune des cinq lettres correspond à un chiffre différent.
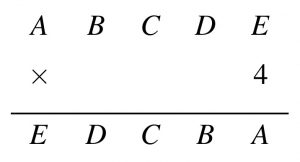
.
Que vaut \(ABCDE\) ?


Solution du quatrième défi
La réponse est : \(ABCDE=21978\)
Remarquons que \(4A<10\), donc \(A\) vaut \(1\) ou \(2\). De plus, comme \(A\) est le chiffre des unités d'un multiple de \(4\), il ne peut pas être égal à \(1\) et donc \(A=2\).
On en déduit alors que \(E=8\) ou \(E=9\) avec une éventuelle retenue, mais le chiffre des unités de \(4\times E\) vaut \(A=2\), ce qui entraîne \(E=8\).
Ensuite, comme \(4B<10\) et comme les chiffres sont tous distincts, on obtient \(B=1\).
Par conséquent, le chiffre des unités de \(4D+3\) est \(1\), ce qui implique que \(D=7\) car \(D\) est différent de \(A=2\).
On en déduit finalement que \(C=9\) et donc \(ABCDE=21978\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


8h54
1er défi
Age de Marie: ab=10a+b
Age de Bruno: cd=10c+d
1000a+100b+10c+d=x²
Dans 31ans:
ab–> ab+31= 10(a+3)+b+1
cd –> cd+31= 10(c+3)+d+1
abcd–> 10(a+3)+100(b+1)+10(c+3)+d+1=y²
y²-x²=(y-x)(y+x)=3000+100+30+1
(y-x)(y+x)=3131=101×31
D’où y=66 et x=36
1000a+100b+10c+d=x²=35²=1225
ab=12 et cd=25
Marie a 12ans
Bruno a 25ans
9h01
Le plus petit âge a \(1\) ou \(2\) chiffre(s). Mais dans le premier cas, l’autre en aurait \(3\), donc en ajoutant \(31\) à chacun on obtiendrait respectivement \(2\) chiffres et au moins \(3\) chiffres, soit au moins \(5\) en tout. Donc les deux âges ont exactement \(2\) chiffres. Alors la différence entre le carré \(a^2\) actuel et le carré futur \(b^2\) est \(31*100 + 31\) :
\(b^2 – a^2 = 3131\)
\( (b – a)(b + a) = 31 * 101 \)
Comme \(31\) et \(101\) sont premiers on a forcément :
\(b – a = 31\)
\(b + a = 101\)
D’où \(2a = – 31 + 101 = 70\), soit \(a = 35\), puis \(b = 35 + 31 = 66\).
Ainsi \(a^2 = 1225\), donc Marie et Bruno ont \(12\) ans et \(25\) ans.
On vérifie que dans \(31\) ans ils auront \(12 + 31 = 43\) ans et \(25 + 31 = 56\) ans, et on a bien \(4356 = 66^2\).
15h26
2e défi
Un cube a douze arêtes, mais nous avons ici onze allumettes seulement.
Construisons donc un cube avec douze allumettes, ôtons une allumette, et il nous reste 4 carrés constitués de onze allumettes.
12h59
Bonjour
Au départ toutes les allumettes sont dans le même plan. Pour obtenir votre cube à 11 allumettes, il faudrait en sortir au moins 7 hors de ce plan, mais l’énoncé autorise seulement 4 déplacements.
Pour ma part j’ai bien obtenu 4 carrés, tous de côté \(\frac{1}{2}\), mais en déplaçant 5 allumettes. Je ne vois aucune solution !
13h07
Bien vu, tout à l’enthousiasme de ma réponse, je n’avais pas lu correctement l’énoncé.
10h12
Haha! L’astuce est de « casser » les carrés existant en remontant les 2 allumettes du bas à 1/2 allumettes et de prendre 2 allumettes du grand carré sur la partie haute afin de former les 4 carrés de longueur 1/2 allumettes.
Le grand carré et les 2 du bas on disparu. On se retrouve bien avec 4 carrés en ayant déplacé que 4 allumettes.
7h49
3e défi
Il y a 7 possibilités de décomposer 36 en un produit de 3 entiers.
Mais 2 combinaisons donnent la même somme quand on additionne les 3 entiers:
6x6x1 9x2x2
Iris ne peut donc pas donner les 3 entiers puisqu’il a 2 solutions
Donc S=13
9h53
Cela ne change ni la démarche ni la conclusion (13 reste la seule ambiguïté pour la somme) mais je compte 8 possibilités (2/2/9, 3/3/4, 2/6/3, 1/2/18, 1/3/12, 1/9/4, 1/1/36 et 1/6/6).