
Analyse de données issues d’examens médicaux, étude de l’évolution du cerveau pour différentes espèces, modélisation du comportement des neurones… Les mathématiques sont très présentes en neurosciences !
Du 27 février au 7 avril 2023, l’Institut Henri Poincaré a ouvert ses portes aux mathématiques du cerveau grâce au programme Processus aléatoires dans le cerveau, des données expérimentales aux mathématiques et vice-versa. Rencontre avec deux des organisateurs et organisatrices de ce programme : Eva Löcherbach (Université Paris 1 Panthéon-Sorbonne) et Christophe Pouzat (CNRS).
Adrien Rossille : Quels sont les principaux axes scientifiques du programme de recherche « Processus aléatoires dans le cerveau » ?
Christophe Pouzat : Ce programme comporte deux thématiques principales. Il y a d’un côté l’analyse de données issues d’examens médicaux, par exemple des électroencéphalogrammes. Parmi les sujets étudiés dans cette thématique, on peut citer la question de la perception de la régularité de rythmes : si une personne écoute des sons avec un certain rythme perturbé par un certain aléa, retrouve-t-on la régularité de ce rythme dans l’activité du cerveau ? Et que se passe-t-il dans l’activité cérébrale si le rythme est modifié sans que la personne s’y attende ?
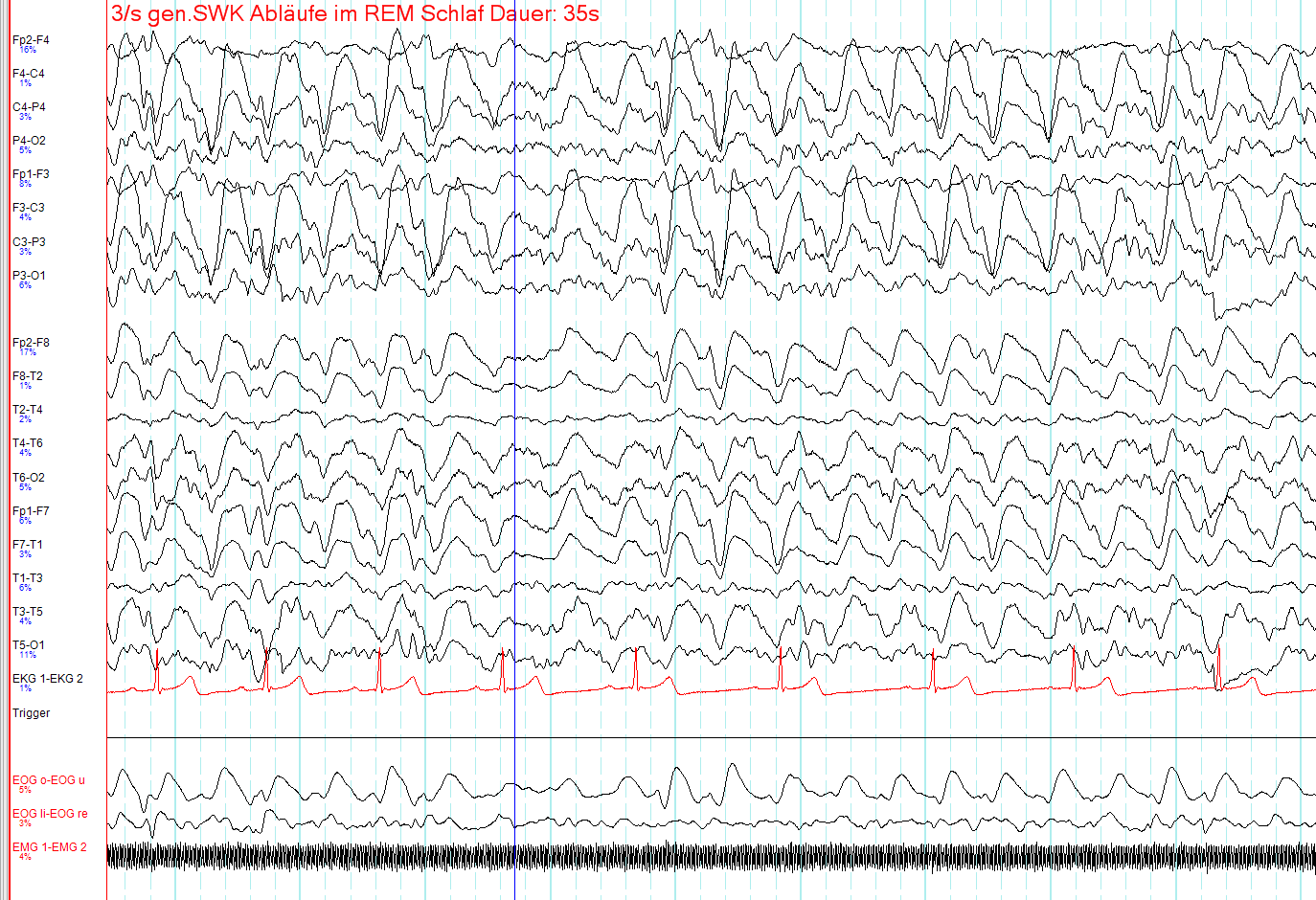
Electroencéphalogramme pendant la phase REM (rapid eye movement) du sommeil
Eva Löcherbach : La seconde thématique se situe dans le domaine des probabilités, pour étudier les interactions entre les neurones : comment transitent les informations, quels neurones influencent lesquels, etc. L’enjeu ici est de déterminer le lien entre les propriétés des neurones à l’échelle individuelle et les propriétés globales du système. C’est une approche analogue à celle de la physique statistique, qui cherche à faire le lien entre le comportement de molécules à l’échelle microscopique et le comportement d’un système, un gaz par exemple, à l’échelle macroscopique.
-
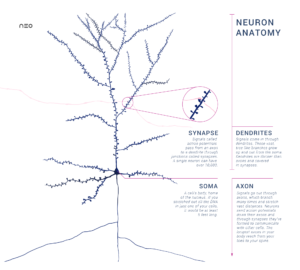
Anatomie d’un neurone
Comment l’approche mathématique a-t-elle émergé dans le domaine des neurosciences ?
Christophe Pouzat : La naissance de cette approche remonte aux années 1940 avec deux scientifiques américains : Warren McCulloch et Walter Pitts. Au début, il s’agissait de montrer que des réseaux de quelques neurones pouvaient effectuer les mêmes opérations que des portes logiques. Cette approche, en plus de son importance pour les neurosciences, a également été à l’origine de l’émergence de l’intelligence artificielle, notamment les réseaux d’apprentissage profond actuels.
Quels sont les outils mathématiques utilisés pour étudier le cerveau ?
Eva Löcherbach : Comme on peut le voir dans les thématiques du programme, les équations différentielles et les probabilités sont au cœur des mathématiques employées en neurosciences. Un autre domaine très important est celui des simulations numériques, qui sont utiles pour effectuer des modélisations du cerveau à grande échelle dans des situations où des preuves formelles ne peuvent pas (pour l’instant) être obtenues. On retrouve aussi la théorie des graphes, dont les graphes aléatoires pour des échelles allant de la zone corticale (1 mm³) au cerveau entier. Enfin, l’étude de la forme tridimensionnelle prise par la surface corticale fait fortement intervenir des notions géométriques et topologiques.
-
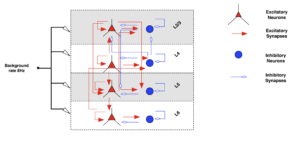
Diagramme d’un réseau de 8 neurones en interactions, avec synapses excitatrices et inhibitrices
Les mathématiciennes et mathématiciens travaillant autour des neurosciences travaillent-ils en lien avec la recherche médicale ?
Christophe Pouzat : Oui, certains scientifiques du domaine travaillent avec des médecins et des patients. Un sujet régulièrement étudié en neurosciences est la maladie de Parkinson, mais on peut citer d’autres exemples, comme la rupture du plexus brachial, qui est une rupture des nerfs allant du haut de la colonne vertébrale, via l’épaule, au bras et à la main, par exemple suite à un accident de moto. D’autres scientifiques étudient la rééducation suite à des greffes de main : comment un patient peut progressivement retrouver la capacité d’effectuer des tâches nécessitant une motricité fine.
Il s’agit pour ces quelques situations de l’étude du cerveau humain. Y a-t-il aussi des recherches sur les cerveaux des animaux ?
Christophe Pouzat : Oui, historiquement c’est même plus par le travail sur des cerveaux d’animaux que les connaissances en neurosciences ont progressé. Les connaissances de base viennent notamment de l’étude des invertébrés marins, comme la seiche, avant que soient étudiés d’autres animaux. De mon côté, j’ai effectué ma thèse sur le cerveau de rat.
Eva Löcherbach : La biophysique de base sur le cerveau est commune à de nombreux animaux. C’est justement en comparant les caractéristiques des cerveaux de différentes espèces animales que l’on peut espérer reconstituer l’évolution du cerveau. Dans le cadre du programme de recherche à l’IHP, c’était notamment le sujet de la conférence ouverte à tous les publics dont l’orateur était Gilles Laurent.
-
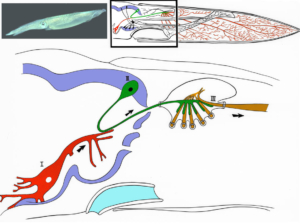
La seiche et son cerveau
Quels sont les enjeux actuels de la recherche mathématique en neurosciences ?
Christophe Pouzat : Pour notre programme scientifique, un vrai enjeu a été d’apprendre à se comprendre entre mathématiciennes et mathématiciens d’un côté, et neuroscientifiques de l’autre. Il faut savoir rester modeste et être prêt à redevenir étudiant dès qu’on aborde un nouveau sujet. Les habitudes de travail sont très différentes entre les deux domaines, car en mathématiques, on a tendance à poser un cadre formel et à construire à partir de là, alors qu’en neurosciences, ou plus généralement en biologie, la formalisation est l’aboutissement d’un long processus empirique.
Eva Löcherbach : Les mathématiques pour les neurosciences servent à donner un cadre pour étudier différents phénomènes et à établir un lien explicite entre ceux-ci. Un exemple, qui a été présenté pendant le programme à l’IHP, est l’étude du comportement de groupes neuronaux suite à des stimulations olfactives. Ce comportement peut être utilement représenté comme une orbite dans un espace d’états. Changer la stimulation, c’est-à-dire changer l’odeur, « déforme » cette orbite.
-
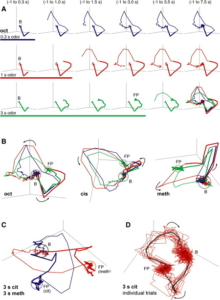
Visualisation de réponses de groupes neuronaux à des stimuli olfactifs



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.