
1. Prologue
Dans une salle d’attente, et pour un petit moment. La lecture ne manque pas mais elle est du même genre comme toujours dans ces endroits-là : des revues datant de quelques années déposées sur une table basse. Les gens n’y lisent rien, ils regardent
simplement les images en attendant leur tour. \c Ca ne m’emballe nullement. Je sors plutôt mon petit cahier fourre-tout où j’ai l’habitude de
loger au crayon presque tout ce qui me passe par la tête. Je commence à regarder un petit exercice que j’ai trouvé par hasard le matin même en feuilletant une revue de vulgarisation des mathématiques. Juste après avoir dégagé les pistes pour le résoudre, j’y ai découvert de belles choses à partir desquelles on peut générer une bonne leçon de didactique, concrète, et donc utile.
Je me suis alors dit qu’il serait plus intéressant
de partager cela avec d’autres, échanger dessus, que
d’écrire un texte standard pour ouvrir un débat (encore une fois) général sur l'{enseignement des mathématiques} ! Voici de quoi il en est question.
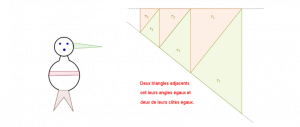
Soit \(\tau=ABC\) un triangle non plat. Alors \(6\) nombres lui sont associés : les mesures \(x\), \(y\) et \(z\) respectivement des
côtés \(BC\), \(CA\) et \(AB\) et celles \(\alpha \), \(\beta \) et \(\gamma \) respectivement des angles \(\widehat A\), \(\widehat B\) et \(\widehat C\).
Trouver deux triangles \(\tau \) et \(\tau’\) non isométriques ayant \(5\) de ces nombres égaux.
Une petite grimace au premier abord : sans jamais faire attention j’ai toujours eu l’image un peu vague que deux triangles ayant les mêmes
angles (donc semblables d’après le troisième cas de similitude) avec en plus un côté égal sont isométriques. Mais je me ressaisis en me disant
que si la question est posée c’est que je me trompais (et que j’aurais dû prendre un peu de temps pour vérifier une fois pour toutes ce qu’il en est réellement).
Je me mets à réfléchir dessus. Et bien sûr la première chose que je vois est que si \(5\) des \(6\) nombres sont égaux, c’est que celui qui diffère est forcément un côté (l’assertion « trois
côtés égaux » implique l’isométrie entre les deux d’après le premier cas d’égalité des triangles).
Puisque un triangle est caractérisé à isométrie près par ses côtés, il sera dorénavant désigné par un triplet \(\tau =\langle x,y,z\rangle \) de nombres réels \(x>0\), \(y>0\) et \(z>0\) tels que \( x< y+z\), \(y < z+x\) et \(z < x+y\). (Les inégalités sont strictes parce que les triangles que nous considérons sont supposés non plats.) La vraie question est donc en fait :
Trouver deux triangles \(\tau \) et \(\tau’\) non isométriques mais semblables et ayant en plus deux de leurs côtés égaux.
2. Résolution.
Les deux triangles \(\tau =\langle x,y,z\rangle \) et \(\tau’ =\langle x’,y’,z’\rangle \) étant semblables,
il existe un nombre réel \(\lambda >0\) tel que \(x’=\lambda x\), \(y’=\lambda y\) et \(z’=\lambda z\).
Nous allons en fait répondre à une question un peu plus générale : trouver toutes les paires \((\tau ,\tau’)\) de triangles \(\tau =\langle x,y,z\rangle \) et \(\tau’ =\langle x’,y’,z’\rangle \)
tels que :
\[\cases{x’=y\cr y’=z}\hskip1cm \hbox{et}\hskip1cm {{x’}\over x}={{y’}\over y}={{z’}\over z}\cdot \]
La résolution (assez facile) de ce problème nous amène à choisir librement \(x\) et \(y\) et prendre nécessairement \(z={{y^2}\over x}\) et \(z’={{y^3}\over {x^2}}\).
A priori, les solutions sont donc de la forme :
\[\tau =\left( x,y,{{y^2}\over x}\right) \hskip0.5cm \hbox{et} \hskip0.5cm \tau’=\left( y,{{y^2}\over x},{{y^3}\over {x^2}}\right) \]
avec \(x\) et \(y\) arbitraires dans \({\Bbb R}_+^\ast .\)
Mais le triplet \(\left( x,y,{{y^2}\over x}\right) \) ne représente un triangle \(\tau \) (non plat) que si ses composantes vérifient les inégalités (strictes) du triangle. Un calcul simple amène à
imposer à \(x\) et \(y\) la condition \({1\over \varphi } <{y\over x}< \varphi \)
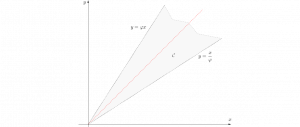
où \(\varphi \) est le nombre d’or- qui vaut \({{\sqrt{5}+1}\over 2}\). Le couple \((x,y)\) ne peut donc être choisi que dans le cône ouvert \({\cal C}\) grisé dans le dessin ci-dessous. Et comme \(x\) doit être différent de \(y\) (les triangles cherchés ne peuvent pas être isocèles), \({\cal C}\) est privé de la première bissectrice.
Finalement, les paires de triangles \((\tau ,\tau’)\) répondant à la question sont (que nous présentons de façon légèrement différente) :
\[\tau =( x,\lambda x,\lambda^2x) \hskip0.5cm \hbox{et} \hskip0.5cm \tau’=(\lambda x,\lambda^2x,\lambda^3x) \]
avec \(x\in {\Bbb R}_+^\ast \) et \(\lambda \in {\Bbb R}_+^\ast \setminus \{ 1\} \)
tel que \({1\over \varphi }<\lambda <\varphi .\)
Les triangles \(\tau_n=\langle \lambda^nx,\lambda^{n+1}x,\lambda^{n+2}x\rangle \) et \(\tau_{n+1}=\langle \lambda^{n+1}x,\lambda^{n+2}x,\lambda^{n+3}x\rangle \) avec \(n\in {\Bbb Z}\)
répondent aussi à la question. Le nombre \(\lambda \in ]\varphi^{-1},\varphi [\) étant donné, prenons \(x=1\) et construisons géométriquement par exemple la paire \((\tau_0,\tau_1)\) en commençant par \(\tau_0\).
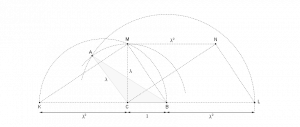
On trace un segment \(BC\) de longueur \(1\). Sur la perpendiculaire en \(C\) à la droite \((BC)\), on repère un
point \(M\) tel que \(CM=\lambda \). La perpendiculaire en \(M\) à \((BM)\) coupe la droite \((BC)\) en un point \(K\) tel que \(CK=\lambda^2\).
On construit le parallélogramme \(CKMN\) ensuite le parallélogramme \(MNLB\) ; le segment \(LB\) mesure donc \(\lambda^2\). Le point \(A\), troisième
sommet du triangle \(\tau_0\) (les deux premiers étant \(B\) et \(C\)) est l’intersection du cercle de centre \(C\) et passant par \(M\) et le cercle
de centre \(B\) et passant par \(L\).

Le triangle \(\tau_1\) s’obtient en appliquant au triangle \(\tau_0\) déjà construit
l’homothétie de centre \(C\) (ou \(A\) ou \(B\)) et de rapport \(\lambda \)
On peut aussi se poser une question supplémentaire :
Parmi toutes ces paires de triangles solutions du problème, y a-t-il des paires de triangles rectangles
Une simple application du théorème de Pythagore montre que de telles paires sont donnés comme suit :
\[\tau =( x,\lambda x,\lambda^2x) \hskip0.5cm \hbox{et} \hskip0.5cm \tau’=(\lambda x,\lambda^2x,\lambda^3x) \]
avec \(x\in {\Bbb R}_+^\ast \)
et \(\lambda =\sqrt{\varphi }\) ou \({1\over {\sqrt{\varphi }}}\)
(On vérifie facilement que les nombres \(\sqrt{\varphi }\) et \({1\over {\sqrt{\varphi }}}\) sont bien dans l’intervalle \(]\varphi^{-1},\varphi [\).) Le rapport des aires
de ces deux triangles (du plus grand au plus petit) est donc exactement le nombre d’or \(\varphi \) !
La frise du dessin du logo de ce billet est formée de tels triangles.
3. Épilogue
Il est clair que je n’ai rien inventé de nouveau à travers cet exercice qui, comme tout le monde peut le remarquer, est vraiment très élémentaire. Et je comprend que quand on n’est pas un « ouvrier de l’enseignement » constamment sur le front, on puisse être amené à se demander quel est son intérêt.
Son intérêt ? Il est riche par tout ce que fait revisiter sa résolution, notamment :
\(\bullet \) Les cas d’égalité et de similitude des triangles. C’est l’occasion de les rappeler. Le moins que je puisse dire est que
la majorité des étudiants que j’ai en Licence 3 et en Master ne savent plus (ou n’ont peut-être jamais su) ce que c’est.
\(\bullet \) Un peu d’analyse élémentaire dans la recherche des solutions d’un problème soumis à des contraintes.
\(\bullet \) L’apparition quelque peu mystérieuse du nombre d’or \(\varphi ={{\sqrt{5}+1}\over 2}\),
de son inverse \({1\over \varphi }={{\sqrt{5}-1}\over 2}\) et de sa racine carrée (pour les paires de triangles rectangles) est une si agréable surprise. Il est encore là ce \(\varphi \) !
La nature est donc bien faite !
\(\bullet \) Des constructions géométriques à la règle et au compas, notamment pour avoir \(\lambda^2\) et \(\lambda^3\) à partir de \(\lambda \)
dès qu’on se donne celui-ci.
Bref… il me semble bien adapté pour un cours de didactique dans les différentes formations des enseignants. C’est aussi
un thème de travail qui pourrait
être développé en Seconde, Première ou Terminale par exemple. Et au-delà de tout ça, il intéresserait sûrement toute personne passionnée par ce genre de mathématiques.
C’est à ces niveaux-là que des avis et des commentaires sont sollicités auprès des lecteurs. Le débat du 18 mars est ouvert, mais sous une forme différente cette fois-ci !





14h33
Voir les 8 commentaires