Devinette en chiffres arabes

Tous les élèves de terminale ont (je pense) rencontré la construction mathématique objet de cet article. J’ai récemment découvert qu’elle était connue depuis bien plus longtemps, en de très multiples endroits. Par exemple, elle est décrite par le mathématicien arabe Ibn Mun‘im.

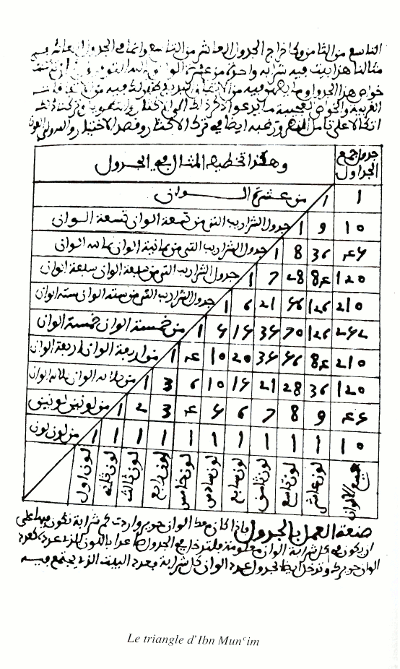
En parcourant un livre ⁴Une histoire de la science arabe, Ahmed Djebbar, points Seuil 2001., mon regard s’est arrêté sur cette reproduction, qui m’a immédiatement frappé car j’ai reconnu de quoi il s’agissait. Je ne lis pas l’arabe, mais regardez plutôt :

Il s’agit de « chiffres arabes ⁵Plus précisément, il s’agit de chiffres arabes du Maghreb, qui ont été repris par les Européens. Les Arabes d’Arabie utilisaient un autre jeu de dix caractères. », que je pouvais donc à peu près lire. Reconnaissez-vous de quoi il s’agit ?

De quoi s’agit-il ? Dans ce triangle, si on numérote les lignes, et les positions dans chaque ligne, à partir de zéro, alors le nombre en position p sur la ligne numéro n indique combien il existe de façons de choisir p objets parmi n. Regardons par exemple la ligne numéro 4 (c’est-à-dire la cinquième ligne, car on a compté en partant du numéro zéro) :

1 4 6 4 1Elle indique que, parmi quatre objets, il y a :

• une façon de ne choisir aucun objet (évidemment),

• quatre façons d’en choisir un seul (encore évidemment : on choisit le premier objet, ou le deuxième, ou le troisième, ou le quatrième),

• six façons d’en choisir deux : comptez-les ! Les deux premiers, le premier et le deuxième, le premier et le troisième etc.

• quatre façons d’en choisir trois : cela revient au même qu’en choisir un et l’éliminer, on revient au deuxième cas examiné, et en passant on comprend pourquoi le triangle est symétrique par rapport à son axe vertical,

• une façon de choisir tous les objets (évidemment).

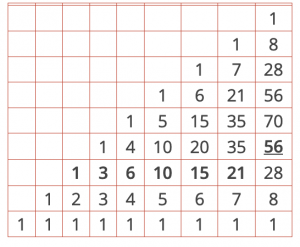
Ce tableau a été dressé par Ahmad ibn Mun‘im al-Abdari, mathématicien des 12^ème et 13^ème siècles du calendrier chrétien, né à Dénia en Andalousie, ayant vécu à Marrakech, et mort en 1228. Quelle est sa découverte ? Il est difficile de compter de but en blanc le nombre de choix possibles de p objets parmi n, dès que n et p dépassent quelques unités. Cependant ces nombres, dits combinaisons de p parmi n, s’organisent dans un tableau triangulaire dont la construction suit une loi très simple. Dans la présentation d’Ibn Mun‘im, chaque nombre est la somme des nombres qui le précèdent, sur la ligne du dessous. Par exemple, le nombre 56, souligné, est la somme des nombres en gras, sur la ligne du dessous :

C’est, je suppose, pour cela que l’auteur a décalé vers le bas la dernière, ou plutôt la première —dans le sens de lecture arabe—, colonne de son tableau. Ainsi on voit que chacune de ses cases porte la somme des nombres des cases précédentes.

Cette propriété du triangle provient d’une propriété plus simple encore. Dans le deuxième schéma que j’ai indiqué, chaque nombre est la somme des deux nombres qui le « précèdent », au dessus à gauche et au-dessus à droite, en comptant comme zéro une absence de nombre, le long des côtés du triangle. Vérifiez vous-mêmes ! J’ignore si Ibn Mun‘im mentionne cette propriété, A. Djebbar n’y fait pas allusion.

A. Djebbar signale enfin que les annotations en marge de ce tableau d’Ibn Mun‘im indiquent le nombre de choix possibles, pour un tisserand, de p couleurs de fil parmi n. C’est probablement une situation concrète prise comme exemple-type pour faire comprendre la situation abstraite. Plus largement, la combinatoire était une discipline en train de naître, dans le monde arabe des 12^ème et 13^ème siècles. Ibn Mun‘im et d’autres mathématiciens arabes de l’époque ont ainsi montré diverses formules sur les combinaisons, avec ou sans répétitions, de p objets parmi n.

Plusieurs personnes m’ont alors signalé qu’il existe à travers le monde de nombreuses traces écrites, directes ou indirectes, du triangle des combinaisons, encore plus anciennes. La plus ancienne est indienne, remonte entre les 5^ème et 2^ème avant notre ère, et son auteur est Pingala. Le triangle n’est pas présenté sous son aspect combinatoire (comptage des combinaisons) mais algébrique (coefficients du binôme). Pour un aperçu de cette histoire et un supplément d’iconographie, merci wikipedia anglophone ou, un peu moins riche mais complémentaire, francophone.

Et Pascal ? Il a redécouvert ce triangle dans ses travaux de dénombrement et de probabilités, exposés dans son célèbre Traité du triangle arithmétique, paru en 1654. Les propriétés du triangle que Pascal dégage —comme la formule dite du « binôme de Newton »— sont très riches, et son traité, très construit, a un caractère fondateur ; il mèle probabilités, combinatoire et algèbre en une unité. Il n’est donc pas illégitime qu’on associe son nom au triangle. Souvenons-nous cependant de ses précurseurs, Ibn Mun‘im dans son traité Fiqh al-hisab, et beaucoup d’autres, connus ou inconnus.

La reproduction du manuscrit arabe me donne aussi l’occasion d’un exercice pour mes étudiants, dans un module de probabilités : reconnaître de quoi il s’agit.

Je profite enfin de ce billet pour soumettre au savant lectorat la question suivante, que m’a inspiré le manuscrit et une question d’un étudiant ⁶Pourquoi Ibn Mun‘im a-t-il ordonné le triangle de gauche à droite, dans le sens de sa construction logique, alors qu’il écrivait de droite à gauche ? C’est comme si nous Européens avions présenté le triangle avec la pointe à droite, se développant vers la gauche … C’est peut-être pour présenter le triangle comme une explication des valeurs de la première colonne —la plus à droite—, « cachée derrière elle ». Je n’ai pas d’autre hypothèse. Si un lecteur en a une …. Les Arabes écrivent de droite à gauche mais, pour écrire un nombre, ordonnent leurs chiffres comme nous : le chiffre des unités à gauche, celui des dizaines s’il y en a, à sa droite, celui des centaines à sa droite etc.Autrement dit, ils écrivent les nombres en commençant par les unités, et nous procédons de façon inverse. Y a-t-il une explication : pourquoi le choix de cet ordre par les Arabes, et pourquoi les Européens l’ont-il gardé visuellement intact, c’est-à-dire renversé, du point de vue de l’acte d’écriture ?